【算法】位运算

目录

1.基础

2.操作

2.1 置位 set bit

2.2 查位check bit

2.3 切换位 toggle bit

2.4 清除位 clear bit

2.5 最右1位掩码

2.6 最左1位掩码

2.7 清除最右1

3.编程题

3.1 leetcode 476. 数字的补数

思路

3.2 leetcode 201. 数字范围按位与

思路

求解方式

---

1.基础

所有的数据以二进制的形式存储，即0、1两种状态，计算机对数据进行的运算(+、-、*、/)都通过位运算实现，且符号位共同参与运算。

位运算	符号	真值表	作用
NOT 非	~	～ 0 0 1 1 0
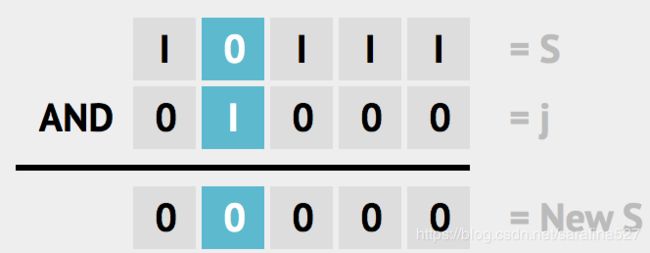
AND 与	&	& 0 1 0 0 0 1 0 1	1.清零 &~(1< 2.check位 &(1< 3.判断奇偶 &1
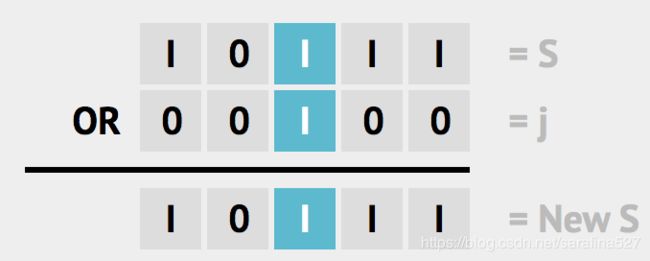
OR 或	|	| 0 1 0 0 1 1 1 1	1.置位 |(1<
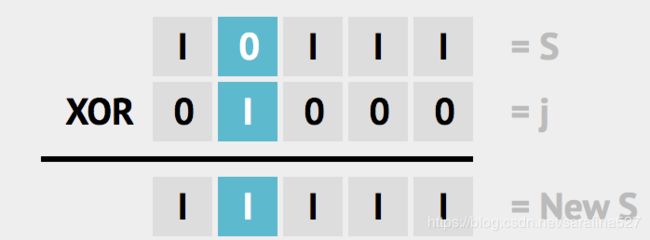
XOR 异或	^	^ 0 1 0 0 1 1 1 0	1.翻转指定位 ^1 2.与0相异或值不变 ^0 3.交换两个数
左移	<<	1<
右移	>>	n>>i 左边补符号位
无符号右移	>>>	n>>i 左边补0

2.操作

对一个整数S，操作其第i位（自右向左，以0位开始），以S=23 (0b00010111)为例，其有效位如下

2.1 置位 set bit

    public static int setBit(int n, int i) {
        return n|(1<

置i=2,newS = S|(1<<2)

2.2 查位check bit

查i=3，是0

    public static boolean checkBit(int n, int i) {
        return (n|(1< 0;
    }

2.3 切换位 toggle bit

    public static int toggleBit(int n, int i) {
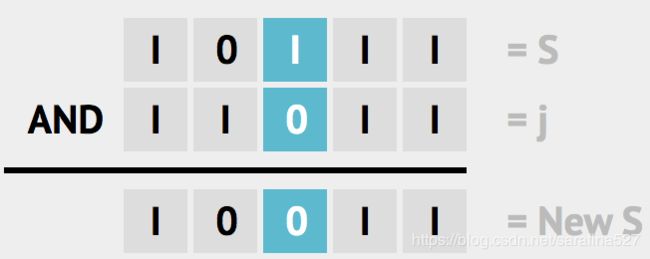
        return n ^ (1<

2.4 清除位 clear bit

    public static int clearBit(int n, int i) {
        return n & ~(1<

2.5 最右1位掩码

    public static int leastOneBit(int n) {
        return n & (~n)+1;
    }

2.6 最左1位掩码

返回i的最高有效位的掩码，如i=00..1xx..，则返回00..100..

JDK的只有6步，即可获得

    public static int highestOneBit(int i) {
        // HD, Figure 3-1
        i |= (i >>  1);
        i |= (i >>  2);
        i |= (i >>  4);
        i |= (i >>  8);
        i |= (i >> 16);
        return i - (i >>> 1);
    }

操作	IN	OUT	解释
i|=i>>1	1xxxxx...	11xxxxx...	最高位复制了1个1到后面 有2个1
i|=i>>2	11xxxx...	1111xxxx...	复制了2个1，最高位有4个1
i|=i>>4	1111xxxx...	11111111xxx...	复制了4个1，最高位有8个1
i|=i>>8	11111111xxx...	1111111111111111xxx...	复制了8个1，最高位有16个1
i|=i>>16	1111111111111111xxx...	11111111...1111	复制了16个1，最高位有有32个1， ps：如果i最高位不足1、2、4、8、16，操作相当于|0，不变 此时的i变成了最高位后全是1，多余的从右边溢出
i - (i >>> 1)	11111111...1111	100000...0000	最高位为1的掩码

2.7 清除最右1

n模式为 xx...100...，则n-1为xx...011...，n&(n-1)则为xx...000...，清除了最后一个1位

    public static int clearLowestBit(int n, int i) {
        return n & (n-1);
    }

3.编程题

3.1 leetcode 476. 数字的补数

给定一个正整数，输出它的补数。补数是对该数的二进制表示取反。

注意:

1. 给定的整数保证在32位带符号整数的范围内。
2. 你可以假定二进制数不包含前导零位。

思路

5的二进制表示为101（没有前导零位），其补数为010。所以你需要输出2。
～101 = 1111...010，前面取反的1不要 ~n & allOneAfterhighestBit(n)

    public int findComplement(int num) {
        if (num==0) return 1;
        else return ~num & allOneAfterhighestBit(num);
    }
    // 后半段均为1
    int allOneAfterhighestBit(int i) {
        i|=i>>1;         // 1xxxxx...最高位复制了一个1到后面 =>11xxxxx... 有2个1
        i|=i>>2;         // 11xxxx...复制了2位1 => 1111xxxx... 有4个1
        i|=i>>4;         // 1111xxxx...复制了4个1 =>11111111xxx... 有8个1
        i|=i>>8;         // 11111111xxx... 复制了8个1 => 1111111111111111xxx... 有16个1
        i|=i>>16;        // 1111111111111111xxx... 复制了16个1 => 11111111...1111 有32个1
        // 如果i最高位不足8或者16等，操作相当于|0，不变，所以此时的i变成了最高位后全是1x
        return i;
    }

3.2 leetcode 201. 数字范围按位与

给定范围 [m, n]，其中 0 <= m <= n <= 2147483647，返回此范围内所有数字的按位与（包含 m, n 两端点）。

思路

• [m,n]递增区间，m=aa..0xxx....,n=aa..1yyy....有着相同前缀，
• 因为在[m,n]=[aa..0xxx....，aa..1yyy....]递增区间内总包含一个数为 aa..100..0，该数与任何数相&后缀都为0
• 解可以分为两断，前缀就是相同前缀aa..，后缀都是0

求解方式

• 求取一个掩码 11..{相同前缀长度}00..00，第一个0是m与n第一个不同的位，不同的位通过异或^可得
• m^n=00...1xx..的第一个不同的位置，其及其后都为0 因为 所以与之后都为0
• 类似与上文2.6 Integer.highestOneBit(n)，allOneAfterhighestBit(m^n)求取掩码
• res = n & ~(highAllone(m^n)) 将m^n高位后全置为1 00..111..11

class Solution {
    public int rangeBitwiseAnd(int m, int n) {
        return n & ~(allOneAfterhighestBit(m^n));
    }
    int allOneAfterhighestBit(int i) {
        i|=i>>1;         // 1xxxxx...最高位复制了一个1到后面 =>11xxxxx... 有2个1
        i|=i>>2;         // 11xxxx...复制了2位1 => 1111xxxx... 有4个1
        i|=i>>4;         // 1111xxxx...复制了4个1 =>11111111xxx... 有8个1
        i|=i>>8;         // 11111111xxx... 复制了8个1 => 1111111111111111xxx... 有16个1
        i|=i>>16;        // 1111111111111111xxx... 复制了16个1 => 11111111...1111 有32个1
        // 如果i最高位不足8或者16等，操作相当于|0，不变，所以此时的i变成了最高位后全是1x
        return i;
    }

}