AES算法描述及C语言实现

前言

AES算法是当前最流行的对称加密算法，也是一种分组加密算法，分组密码就是把明文分为固定长度的一组一组，每次加密一组数据，直到加密完整个明文数据。AES算法根据分组长度可以分为AES128, AES192，AES256，其所要求的秘钥长度和加密轮数也各不相同。鉴于这三种模式的算法在本质上没有区别，所以本文主要介绍AES-128（数据分组为16字节，秘钥长度为16字节，加密轮数为10轮），并给出C语言实现。

确切的说分组密码只是规定了怎么加密一组明文，如果明文数据比较长，其他的组需要怎么进行加密取决于使用何种分组密码工作模式。对于AES-128而言，每次只加密16字节长度的数据，如果明文长度为32字节话，我们很容易想到第2组16字节可以仿照第1组16字节数据进行处理，这就是最简单的分组密码工作模式ECB（电子密码本）模式，本文主要讲述AES算法实现，对于长数据也是使用这种最简单的ECB分组处理方式，更多其他分组密码工作模式，请参考另一篇文章图解分组密码五大工作模式。

前面讨论的数据长度都是16字节，或者其整倍数长度的加密算法实现，对于数据长度不是分组长度整倍数的情形，通常需要对数据进行填充，使其长度达到分组长度的整倍数再来进行加密。对于数据长度不足分组长度整倍数使用何种格式进行数据填充有多种不同的填充标准，比如在数据后面填充二进制的0x0，直到达到要求的长度，这就是ZeroPadding方式；比如数据缺少几位就填充二进制的几，例如缺少4位填充0x04 0x04 0x04 0x04，这就是PKCS7/PKCS5填充方式。本文提供的实现不涉及数据填充，假定明文数据都是16字节的整倍数长度。

AES算法流程

AES算法主要可以分为秘钥扩展、字节替换、行移位、列混合和轮秘钥加这5个步骤。

• 秘钥扩展（KeyExpansions：给定的初始秘钥一般比较短，比如16字节，而算法如果进行10轮运算的话就需要16x(10+1)字节长度的秘钥，需要对原始秘钥进行秘钥扩展。
• 字节替换（SubBytes）：一个非线性的替换步骤，根据查表把一个字节替换为另一个字节。
• 行移位（ShiftRows）：将数据矩阵的每一行循环移位一定长度。
• 列混合（MixColumns）：将数据矩阵乘以一个固定的矩阵，增加混淆程度。
• 轮秘钥加（AddRoundKey）:将数据矩阵与秘钥矩阵进行异或操作。

AES加密

AES-128加密流程可以使用如下伪代码表示：

AES-128加密(uint8 in[16], uint8 out[16], uint8 key[16]){
  uint8 state[4,4] = in;
  uint32 w[44] = KeyExpansions(key[16]);

  addRoundKey(state, w[0-3]);

  for (int j = 1; j < 10; ++j) {
    subBytes(state);
    shiftRows(state);
    mixColumns(state);
    addRoundKey(state, w); //w[4-7],w[8-11]...w[37-40]
  }

  subBytes(state);
  shiftRows(state);
  addRoundKey(state, w[41-44]);
  out = state;
}

AES解密

AES-128解密流程可以使用如下伪代码表示:

AES-128解密(uint8 in[16], uint8 out[16], uint8 key[16]){
  uint8 state[4,4] = in;
  uint32 w[44] = KeyExpansions(key[16]);
  //此时使用的秘钥是加密时使用的秘钥的倒序
  addRoundKey(state, w[41-44]);

  for (int j = 1; j < 10; ++j) {
    inverse-subBytes(state);
    inverse-shiftRows(state);
    inverse-mixColumns(state);
    addRoundKey(state, w); //w[37-40], ... w[8-11],w[4-7],...
  }

  inverse-subBytes(state);
  inverse-shiftRows(state);
  addRoundKey(state, w[0-3]);
  out = state;
}

AES算法步骤

前提

AES运算都是以下4x4字节表示的二维数组矩阵uint8_t state[4][4]为一个单位，把一个连续的序列"1234567890abcdef"放在矩阵中，对应的顺序为下图所示。一定要注意 排列的顺序是竖排的，不是横排的！

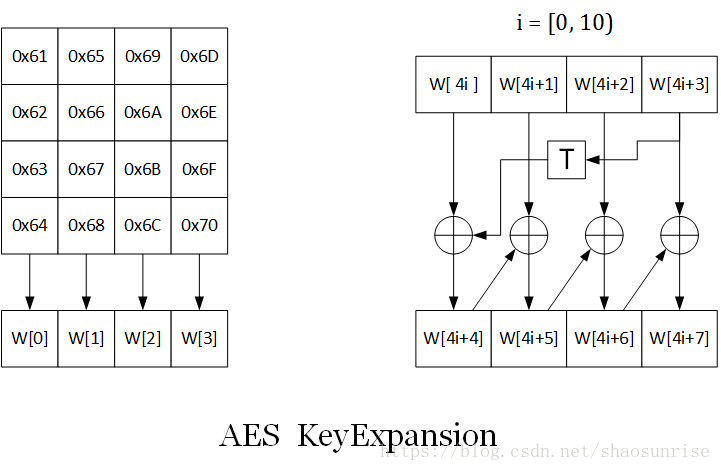
秘钥扩展 KeyExpansion

示例秘钥key = “abcdefghijklmnop”={0x61, 0x62,…,0x6F,0x70}。
AES128中原始秘钥key为16字节，运算中需要11个矩阵大小的秘钥，每一列所包含的32位记为一个uint32_t W，所以秘钥扩展一共需要生产44个列W，即uint32_t W[44]。

W[0-3]为直接复制的原始秘钥。

• W[0] = 0x61626364.
• W[1] = 0x65666768.
• W[2] = 0x696A6B6C.
• W[3] = 0x6D6E6F70.

W[4-43]为扩展的秘钥。

$$\text{W[n]}=\{\begin{array}{ll}\text{W[n-4]}\oplus \text{W[n-1]},& \text{if n != 4的倍数}.\\ \text{W[n-4]}\oplus \text{Mix(W[n-1])}\oplus \text{rcon[(n/4) - 1]},& \text{if n == 4的倍数}.\end{array}$$

$\text{Mix}(x)=\text{SubWord}(\text{RotWord}(x))$

RotWord()为循环左移一位，如输入0x12345678，输出0x34567812。

SubWord()为字节替换，可以参考字节替换。

rcon为轮常量异或，常量数组为：

static const uint32_t rcon[10] = {
        0x01000000UL, 0x02000000UL, 0x04000000UL, 0x08000000UL, 0x10000000UL,
        0x20000000UL, 0x40000000UL, 0x80000000UL, 0x1B000000UL, 0x36000000UL
};

秘钥key = “abcdefghijklmnop”，秘钥扩展后生成的扩展秘钥uint32_t W[44]为：

W[ 0-3 ] 61626364 65666768 696A6B6C 6D6E6F70   
W[ 4-7 ] FFCA3258 9AAC5530 F3C63E5C 9EA8512C   
W[ 8-11] 3F1B4353 A5B71663 5671283F C8D97913   
W[12-15] 0EAD3EBB AB1A28D8 FD6B00E7 35B279F4   
W[16-19] 311B812D 9A01A9F5 676AA912 52D8D0E6   
W[20-23] 406B0F2D DA6AA6D8 BD000FCA EFD8DF2C   
W[24-27] 01F57EF2 DB9FD82A 669FD7E0 894708CC   
W[28-31] E1C53555 3A5AED7F 5CC53A9F D5823253   
W[32-35] 72E6D856 48BC3529 14790FB6 C1FB3DE5   
W[36-39] 66C1012E 2E7D3407 3A043BB1 FBFF0654   
W[40-43] 46AE2121 68D31526 52D72E97 A92828C3   

字节替换 SubBytes

字节替换就是简单的查表操作，AES定义了加密用的S盒和解密用的逆S盒来进行字节替换。

S盒为256个元素的数组，即1个字节（0x00~0xff）可以表示的数量，所以进行字节替换时可以直接把该字节的值作为S盒数组的下标来进行替换。比如0x03字节替换结果为S[0x03]=0x7B，逆S盒同理。图示中$b_{2,2}=S[a_{2,2}]$。

看到有的地方把S盒定义为16x16二维数组S[16][16]，字节替换时取该字节的高4位作为行下标，低4位作为列下标。这种方式因为还得对需要替换字节分别取高低位，得到结果再合并高低位，无疑把字节替换操作复杂化了。采用S[256]一维数组完全可以省去这些不必要的操作。

S盒为

unsigned char S[256] = {
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
};

解密时逆字节替换就是使用逆S盒进行字节替换，逆S盒为：

unsigned char inv_S[256] = {
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D
};

行移位 ShiftRows

前面已经说过，AES运算都是基于4x4二维数组进行的。行移位操作为：第0行不移动，第1行循环左移1字节，第2行循环左移2字节，第3行循环左移3字节。

解密时逆行移位操作为：第0行不移动，第1行循环右移1字节，第2行循环右移2字节，第3行循环右移3字节。

列混合 MixColumns

列混合通过矩阵相乘来实现，经过移位后的矩阵左乘一个固定的矩阵，得到混淆后的矩阵，如下公式所示

$$
\begin{bmatrix}
b_{0,0} & b_{0,1} & b_{0,2} & b_{0,3} \
b_{1,0} & b_{1,1} & b_{1,2} & b_{1,3} \
b_{2,0} & b_{2,1} & b_{2,2} & b_{2,3} \
b_{3,0} & b_{3,1} & b_{3,2} & b_{3,3} \
\end{bmatrix}

\begin{bmatrix}
2 & 3 & 1 & 1 \
1 & 2 & 3 & 1 \
1 & 1 & 2 & 3 \
3 & 1 & 1 & 2 \
\end{bmatrix}
\begin{bmatrix}
a_{0,0} & a_{0,1} & a_{0,2} & a_{0,3} \
a_{1,0} & a_{1,1} & a_{1,2} & a_{1,3} \
a_{2,0} & a_{2,1} & a_{2,2} & a_{2,3} \
a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} \
\end{bmatrix}
$$

上述矩阵相乘可以化简为如下表达式：

$$\{\begin{array}{l}{b}_{0,j}=(2\ast a_{0,j})\oplus (3\ast a_{1,j})\oplus a_{2,j}\oplus a_{3,j}\\ b_{0,j}=a_{0,j}\oplus (2\ast a_{1,j})\oplus (3\ast a_{2,j})\oplus a_{3,j}\\ b_{0,j}=a_{0,j}\oplus a_{1,j}\oplus (2\ast a_{2,j})\oplus (3\ast a_{3,j})\\ b_{0,j}=(3\ast a_{0,j})\oplus a_{1,j}\oplus a_{2,j}\oplus (2\ast a_{3,j})\end{array}$$

其中矩阵的乘法和加法并不是通常意义上的乘法和加法，而是定义在伽罗华域上的二元运算，且使用的不可约多项式为$P(x)=x^8+x^4+x^3+x+1$。关于伽罗华域运算我在另一篇文章中有详细介绍《伽罗华域运算及C语言实现》。其加法为模二加法，相当于异或运算，其乘法可以使用GMul表示，则上式运算可以表示为：

$$\{\begin{array}{l}{b}_{0,j}=\text{GMul}(2,a_{0,j})\wedge \text{GMul}(3,a_{1,j})\wedge (a_{2,j})\wedge (a_{3,j})\\ b_{0,j}=(a_{0,j})\wedge \text{GMul}(2,a_{1,j})\wedge \text{GMul}(3,a_{2,j})\wedge (a_{3,j})\\ b_{0,j}=(a_{0,j})\wedge (a_{1,j})\wedge \text{GMul}(2,a_{2,j})\wedge \text{GMul}(3,a_{3,j})\\ b_{0,j}=\text{GMul}(3,a_{0,j})\wedge (a_{1,j})\wedge (a_{2,j})\wedge \text{GMul}(2,a_{3,j})\end{array}$$

解密时逆列混合操作和列混合一样，只是左乘的矩阵使用如下矩阵。可以验证此矩阵B是列混合使用矩阵A的逆矩阵，两者乘积为单位矩阵，即AB=BA=E。

$$\left[\begin{array}{cccc}\text{0E}& \text{0B}& \text{0D}& \text{09}\\ \text{09}& \text{0E}& \text{0B}& \text{0D}\\ \text{0D}& \text{09}& \text{0E}& \text{0B}\\ \text{0B}& \text{0D}& \text{09}& \text{0E}\end{array}\right]$$

轮秘钥加 AddRoundKey

轮秘钥加是将数据与相应的秘钥逐位进行异或操作。上面已经讲到扩展后的秘钥结构为uint32_t W[44]，轮秘钥加操作取16字节长度的秘钥，即取uint32_t W[4]作为一个单元，把这个总长度为16字节的秘钥按照加密数据同样的格式写成uint8_t b[4][4]二维数组矩阵，然后将此4x4矩阵与4x4的数据矩阵逐位进行异或操作。
如下图所示，$a_{i,j}$表示数据矩阵，$b_{i,j}$表示秘钥，比如W[0]=$b_{0,0}{b}_{1,0}{b}_{2,0}{b}_{3,0}$，W[1]=$b_{0,1}{b}_{1,1}{b}_{2,1}{b}_{3,1}$，W[0]=$b_{0,2}{b}_{1,2}{b}_{2,2}{b}_{3,2}$，W[0]=$b_{0,3}{b}_{1,3}{b}_{2,3}{b}_{3,3}$。

AES-128 C语言实现

#include 
#include 
#include 

typedef struct{
    uint32_t eK[44], dK[44];    // encKey, decKey
    int Nr; // 10 rounds
}AesKey;

#define BLOCKSIZE 16  //AES-128分组长度为16字节

// uint8_t y[4] -> uint32_t x
#define LOAD32H(x, y) \
  do { (x) = ((uint32_t)((y)[0] & 0xff)<<24) | ((uint32_t)((y)[1] & 0xff)<<16) | \
             ((uint32_t)((y)[2] & 0xff)<<8)  | ((uint32_t)((y)[3] & 0xff));} while(0)

// uint32_t x -> uint8_t y[4]
#define STORE32H(x, y) \
  do { (y)[0] = (uint8_t)(((x)>>24) & 0xff); (y)[1] = (uint8_t)(((x)>>16) & 0xff);   \
       (y)[2] = (uint8_t)(((x)>>8) & 0xff); (y)[3] = (uint8_t)((x) & 0xff); } while(0)

// 从uint32_t x中提取从低位开始的第n个字节
#define BYTE(x, n) (((x) >> (8 * (n))) & 0xff)

/* used for keyExpansion */
// 字节替换然后循环左移1位
#define MIX(x) (((S[BYTE(x, 2)] << 24) & 0xff000000) ^ ((S[BYTE(x, 1)] << 16) & 0xff0000) ^ \
                ((S[BYTE(x, 0)] << 8) & 0xff00) ^ (S[BYTE(x, 3)] & 0xff))

// uint32_t x循环左移n位
#define ROF32(x, n)  (((x) << (n)) | ((x) >> (32-(n))))
// uint32_t x循环右移n位
#define ROR32(x, n)  (((x) >> (n)) | ((x) << (32-(n))))

/* for 128-bit blocks, Rijndael never uses more than 10 rcon values */
// AES-128轮常量
static const uint32_t rcon[10] = {
        0x01000000UL, 0x02000000UL, 0x04000000UL, 0x08000000UL, 0x10000000UL,
        0x20000000UL, 0x40000000UL, 0x80000000UL, 0x1B000000UL, 0x36000000UL
};
// S盒
unsigned char S[256] = {
        0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
        0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
        0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
        0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
        0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
        0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
        0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
        0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
        0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
        0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
        0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
        0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
        0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
        0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
        0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
        0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16
};

//逆S盒
unsigned char inv_S[256] = {
        0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
        0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
        0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
        0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
        0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
        0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
        0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
        0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
        0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
        0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
        0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
        0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
        0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
        0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
        0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
        0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D
};

/* copy in[16] to state[4][4] */
int loadStateArray(uint8_t (*state)[4], const uint8_t *in) {
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            state[j][i] = *in++;
        }
    }
    return 0;
}

/* copy state[4][4] to out[16] */
int storeStateArray(uint8_t (*state)[4], uint8_t *out) {
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            *out++ = state[j][i];
        }
    }
    return 0;
}
//秘钥扩展
int keyExpansion(const uint8_t *key, uint32_t keyLen, AesKey *aesKey) {

    if (NULL == key || NULL == aesKey){
        printf("keyExpansion param is NULL\n");
        return -1;
    }

    if (keyLen != 16){
        printf("keyExpansion keyLen = %d, Not support.\n", keyLen);
        return -1;
    }

    uint32_t *w = aesKey->eK;  //加密秘钥
    uint32_t *v = aesKey->dK;  //解密秘钥

    /* keyLen is 16 Bytes, generate uint32_t W[44]. */

    /* W[0-3] */
    for (int i = 0; i < 4; ++i) {
        LOAD32H(w[i], key + 4*i);
    }

    /* W[4-43] */
    for (int i = 0; i < 10; ++i) {
        w[4] = w[0] ^ MIX(w[3]) ^ rcon[i];
        w[5] = w[1] ^ w[4];
        w[6] = w[2] ^ w[5];
        w[7] = w[3] ^ w[6];
        w += 4;
    }

    w = aesKey->eK+44 - 4;
    //解密秘钥矩阵为加密秘钥矩阵的倒序，方便使用，把ek的11个矩阵倒序排列分配给dk作为解密秘钥
    //即dk[0-3]=ek[41-44], dk[4-7]=ek[37-40]... dk[41-44]=ek[0-3]
    for (int j = 0; j < 11; ++j) {

        for (int i = 0; i < 4; ++i) {
            v[i] = w[i];
        }
        w -= 4;
        v += 4;
    }

    return 0;
}

// 轮秘钥加
int addRoundKey(uint8_t (*state)[4], const uint32_t *key) {
    uint8_t k[4][4];

    /* i: row, j: col */
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            k[i][j] = (uint8_t) BYTE(key[j], 3 - i);  /* 把 uint32 key[4] 先转换为矩阵 uint8 k[4][4] */
            state[i][j] ^= k[i][j];
        }
    }

    return 0;
}

//字节替换
int subBytes(uint8_t (*state)[4]) {
    /* i: row, j: col */
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            state[i][j] = S[state[i][j]]; //直接使用原始字节作为S盒数据下标
        }
    }

    return 0;
}

//逆字节替换
int invSubBytes(uint8_t (*state)[4]) {
    /* i: row, j: col */
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            state[i][j] = inv_S[state[i][j]];
        }
    }
    return 0;
}

//行移位
int shiftRows(uint8_t (*state)[4]) {
    uint32_t block[4] = {0};

    /* i: row */
    for (int i = 0; i < 4; ++i) {
    //便于行循环移位，先把一行4字节拼成uint_32结构，移位后再转成独立的4个字节uint8_t
        LOAD32H(block[i], state[i]);
        block[i] = ROF32(block[i], 8*i);
        STORE32H(block[i], state[i]);
    }

    return 0;
}

//逆行移位
int invShiftRows(uint8_t (*state)[4]) {
    uint32_t block[4] = {0};

    /* i: row */
    for (int i = 0; i < 4; ++i) {
        LOAD32H(block[i], state[i]);
        block[i] = ROR32(block[i], 8*i);
        STORE32H(block[i], state[i]);
    }

    return 0;
}

/* Galois Field (256) Multiplication of two Bytes */
// 两字节的伽罗华域乘法运算
uint8_t GMul(uint8_t u, uint8_t v) {
    uint8_t p = 0;

    for (int i = 0; i < 8; ++i) {
        if (u & 0x01) {    //
            p ^= v;
        }

        int flag = (v & 0x80);
        v <<= 1;
        if (flag) {
            v ^= 0x1B; /* x^8 + x^4 + x^3 + x + 1 */
        }

        u >>= 1;
    }

    return p;
}

// 列混合
int mixColumns(uint8_t (*state)[4]) {
    uint8_t tmp[4][4];
    uint8_t M[4][4] = {{0x02, 0x03, 0x01, 0x01},
                       {0x01, 0x02, 0x03, 0x01},
                       {0x01, 0x01, 0x02, 0x03},
                       {0x03, 0x01, 0x01, 0x02}};

    /* copy state[4][4] to tmp[4][4] */
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j){
            tmp[i][j] = state[i][j];
        }
    }

    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {  //伽罗华域加法和乘法
            state[i][j] = GMul(M[i][0], tmp[0][j]) ^ GMul(M[i][1], tmp[1][j])
                        ^ GMul(M[i][2], tmp[2][j]) ^ GMul(M[i][3], tmp[3][j]);
        }
    }

    return 0;
}

// 逆列混合
int invMixColumns(uint8_t (*state)[4]) {
    uint8_t tmp[4][4];
    uint8_t M[4][4] = {{0x0E, 0x0B, 0x0D, 0x09},
                       {0x09, 0x0E, 0x0B, 0x0D},
                       {0x0D, 0x09, 0x0E, 0x0B},
                       {0x0B, 0x0D, 0x09, 0x0E}};  //使用列混合矩阵的逆矩阵

    /* copy state[4][4] to tmp[4][4] */
    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j){
            tmp[i][j] = state[i][j];
        }
    }

    for (int i = 0; i < 4; ++i) {
        for (int j = 0; j < 4; ++j) {
            state[i][j] = GMul(M[i][0], tmp[0][j]) ^ GMul(M[i][1], tmp[1][j])
                          ^ GMul(M[i][2], tmp[2][j]) ^ GMul(M[i][3], tmp[3][j]);
        }
    }

    return 0;
}

// AES-128加密接口，输入key应为16字节长度，输入长度应该是16字节整倍数，
// 这样输出长度与输入长度相同，函数调用外部为输出数据分配内存
int aesEncrypt(const uint8_t *key, uint32_t keyLen, const uint8_t *pt, uint8_t *ct, uint32_t len) {

    AesKey aesKey;
    uint8_t *pos = ct;
    const uint32_t *rk = aesKey.eK;  //解密秘钥指针
    uint8_t out[BLOCKSIZE] = {0};
    uint8_t actualKey[16] = {0};
    uint8_t state[4][4] = {0};

    if (NULL == key || NULL == pt || NULL == ct){
        printf("param err.\n");
        return -1;
    }

    if (keyLen > 16){
        printf("keyLen must be 16.\n");
        return -1;
    }

    if (len % BLOCKSIZE){
        printf("inLen is invalid.\n");
        return -1;
    }

    memcpy(actualKey, key, keyLen);
    keyExpansion(actualKey, 16, &aesKey);  // 秘钥扩展

	// 使用ECB模式循环加密多个分组长度的数据
    for (int i = 0; i < len; i += BLOCKSIZE) {
		// 把16字节的明文转换为4x4状态矩阵来进行处理
        loadStateArray(state, pt);
        // 轮秘钥加
        addRoundKey(state, rk);

        for (int j = 1; j < 10; ++j) {
            rk += 4;
            subBytes(state);   // 字节替换
            shiftRows(state);  // 行移位
            mixColumns(state); // 列混合
            addRoundKey(state, rk); // 轮秘钥加
        }

        subBytes(state);    // 字节替换
        shiftRows(state);  // 行移位
        // 此处不进行列混合
        addRoundKey(state, rk+4); // 轮秘钥加
		
		// 把4x4状态矩阵转换为uint8_t一维数组输出保存
        storeStateArray(state, pos);

        pos += BLOCKSIZE;  // 加密数据内存指针移动到下一个分组
        pt += BLOCKSIZE;   // 明文数据指针移动到下一个分组
        rk = aesKey.eK;    // 恢复rk指针到秘钥初始位置
    }
    return 0;
}

// AES128解密， 参数要求同加密
int aesDecrypt(const uint8_t *key, uint32_t keyLen, const uint8_t *ct, uint8_t *pt, uint32_t len) {
    AesKey aesKey;
    uint8_t *pos = pt;
    const uint32_t *rk = aesKey.dK;  //解密秘钥指针
    uint8_t out[BLOCKSIZE] = {0};
    uint8_t actualKey[16] = {0};
    uint8_t state[4][4] = {0};

    if (NULL == key || NULL == ct || NULL == pt){
        printf("param err.\n");
        return -1;
    }

    if (keyLen > 16){
        printf("keyLen must be 16.\n");
        return -1;
    }

    if (len % BLOCKSIZE){
        printf("inLen is invalid.\n");
        return -1;
    }

    memcpy(actualKey, key, keyLen);
    keyExpansion(actualKey, 16, &aesKey);  //秘钥扩展，同加密

    for (int i = 0; i < len; i += BLOCKSIZE) {
        // 把16字节的密文转换为4x4状态矩阵来进行处理
        loadStateArray(state, ct);
        // 轮秘钥加，同加密
        addRoundKey(state, rk);

        for (int j = 1; j < 10; ++j) {
            rk += 4;
            invShiftRows(state);    // 逆行移位
            invSubBytes(state);     // 逆字节替换，这两步顺序可以颠倒
            addRoundKey(state, rk); // 轮秘钥加，同加密
            invMixColumns(state);   // 逆列混合
        }

        invSubBytes(state);   // 逆字节替换
        invShiftRows(state);  // 逆行移位
        // 此处没有逆列混合
        addRoundKey(state, rk+4);  // 轮秘钥加，同加密

        storeStateArray(state, pos);  // 保存明文数据
        pos += BLOCKSIZE;  // 输出数据内存指针移位分组长度
        ct += BLOCKSIZE;   // 输入数据内存指针移位分组长度
        rk = aesKey.dK;    // 恢复rk指针到秘钥初始位置
    }
    return 0;
}

上面是AES-128加解密算法的实现，下面给出使用方法和测试用例：

#include 
// 方便输出16进制数据
void printHex(uint8_t *ptr, int len, char *tag) {
    printf("%s\ndata[%d]: ", tag, len);
    for (int i = 0; i < len; ++i) {
        printf("%.2X ", *ptr++);
    }
    printf("\n");
}

int main() {

    // case 1
    const uint8_t key[16] = {0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c};
    const uint8_t pt[16]={0x32, 0x43, 0xf6, 0xa8, 0x88, 0x5a, 0x30, 0x8d, 0x31, 0x31, 0x98, 0xa2, 0xe0, 0x37, 0x07, 0x34};
    uint8_t ct[16] = {0};     // 外部申请输出数据内存，用于加密后的数据
    uint8_t plain[16] = {0};  // 外部申请输出数据内存，用于解密后的数据

    aesEncrypt(key, 16, pt, ct, 16); // 加密
    printHex(pt, 16, "plain data:"); // 打印初始明文数据
    printf("expect cipher:\n39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32\n");  // 正常解密后的数据内容

    printHex(ct, 16, "after encryption:");  // 打印加密后的密文

    aesDecrypt(key, 16, ct, plain, 16);       // 解密
    printHex(plain, 16, "after decryption:"); // 打印解密后的明文数据

    // case 2
    // 16字节字符串形式秘钥
    const uint8_t key2[]="1234567890123456";
    // 32字节长度字符串明文
    const uint8_t *data = (uint8_t*)"abcdefghijklmnopqrstuvwxyz123456";  
    uint8_t ct2[32] = {0};    //外部申请输出数据内存，用于存放加密后数据
    uint8_t plain2[32] = {0}; //外部申请输出数据内存，用于存放解密后数据
    //加密32字节明文
    aesEncrypt(key2, 16, data, ct2, 32); 

    printf("\nplain text:\n%s\n", data);
    printf("expect ciphertext:\nfcad715bd73b5cb0488f840f3bad7889\n");
    printHex(ct2, 32, "after encryption:");
    
    // 解密32字节密文
    aesDecrypt(key2, 16, ct2, plain2, 32);  
    // 打印16进制形式的解密后的明文
    printHex(plain2, 32, "after decryption:"); 

    // 因为加密前的数据为可见字符的字符串，打印解密后的明文字符，与加密前明文进行对比
    printf("output plain text\n");
    for (int i = 0; i < 32; ++i) {
        printf("%c ", plain2[i]);
    }

    return 0;
}

下面为程序运行后的测试结果，可以看到明文加密再解密后的数据和加密前的数据是一样的。

plain data:
data[16]: 32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 
expect cipher:
39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32
after encryption:
data[16]: 39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 
after decryption:
data[16]: 32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 

plain text:
abcdefghijklmnopqrstuvwxyz123456
expect ciphertext:
fcad715bd73b5cb0488f840f3bad7889
after encryption:
data[32]: FC AD 71 5B D7 3B 5C B0 48 8F 84 0F 3B AD 78 89 D0 E7 09 D0 FF D3 8C 6D FE C5 5C CB 9F 47 5B 01 
after decryption:
data[32]: 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 70 71 72 73 74 75 76 77 78 79 7A 31 32 33 34 35 36 
output plain text
a b c d e f g h i j k l m n o p q r s t u v w x y z 1 2 3 4 5 6 
Process finished with exit code 0

代码完整的工程已上传到Github仓库：https://github.com/lmshao/AES。

后记

好久之前就看过AES算法的介绍，总是感觉特别复杂特别烦琐，后来想想自己要是能用代码实现一遍印象肯定特别深刻，经过了多天的研究，查看了很多资料和别人家的代码终于把用代码实现了AES-128算法。感觉只是写出了代码可能时间长就忘了，要是能用文字做个笔记总结一下肯定印象更深刻，于是乎就有了这篇文章。

由于之前有很多人总结的太好了，所以就借鉴了很多其他人的东西。包括看了多遍这篇博客《AES加密算法的详细介绍与实现》，写的实在太好了！非常详细！秘钥扩展那一节的图片就是借用他的，我没事又兴致勃勃地用Visio重新画了一遍。还反复查看了多遍AES标准文档和维基百科的AES介绍，其他的图片都直接链接的维基百科的图片。

看别人的文章，然后动手实现一遍是记住这个算法比较好的一个方法，因为总会遇到不曾考虑过的细节。比如AES算法中用的4x4状态矩阵与一维数组的映射关系，状态矩阵是按列的顺序排列的。多次计算出来的结果都不正确，好在AES标准文档给出了测试用例每一个步骤之后的状态矩阵，我就一步一步进行对照查找问题所在。

代码完整的工程已上传到Github仓库：https://github.com/lmshao/AES。有问题欢迎留言交流。

参考

• 维基百科 Advanced Encryption Standard

• AES标准文档 FIPS 197, Advanced Encryption Standard (AES) - CSRC

• CSDN博客 AES加密算法的详细介绍与实现

• Libtom AES代码