基于Pytorch的卷积神经网络剪枝
本篇博客对网络剪枝的实现方法主要在https://jacobgil.github.io/deeplearning/pruning-deep-learning的基础上进行了相应修改而完成,所参考的论文为https://arxiv.org/abs/1611.06440。本篇博客所使用的代码见https://github.com/PolarisShi/purning。
网络剪枝个人觉得是一种实用性非常强的网络压缩方法,并且可以和其它模型压缩方法如网络蒸馏、参数位压缩等进行组合,在保留网络识别精度的同时极大幅度的减少网络在使用时的计算量。但是这种简单粗暴实用的方法,虽然在16年就已经提出了,在网上能够找到的资料反而相对较少。根据jacobgil的分析,可能的原因有:1、目前对剪枝的评价方法(决定哪一些参数应该被删除)还不够完善。2、以目前的框架很难实现网络的剪枝。3、各路大神都把这类网络压缩方法作为自己的大招秘而不宣。个人觉得,第2点才是主要原因。。。jacobgil大神采用python2+pytorch实现了对VGG16网络的压缩,不过正因为算法实现较为复杂,所以对于不同的网络结构,还是要对算法做相应调整,不过只要理解了算法修改起来还是很容易的。
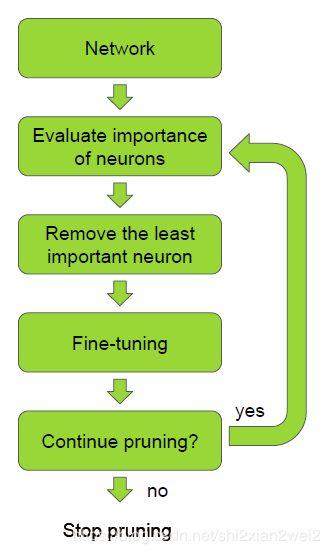
剪枝算法的原理非常简单,如论文中下图所示:
对于一个训练完毕的网络,首先评价各神经元的重要性,把重要性最低神经元移除,之后微调网络,循环上述三个步骤直到网络达到预定目标。所以问题主要在于两个部分,即如何评价各神经元重要性,以及怎么实现移除神经元。
考虑一组训练集D(包含输入X和输出Y),网络的参数W(包含weight和bias)被优化以使得代价函数C(D|W)最小。那么对神经元h重要性的判断就是将神经元h置0,此时代价函数变为:C(D|W, h=0)。我们需要让剪枝前后网络模型的代价函数尽可能的相似,因此我们实质上是依次找出使函数abs( C(D|W) - C(D|W, h=0) )最小的h,之后依次删除。
下面主要结合jacobgil大神的实现方法说一说怎么实现对我们自己的模型的剪枝。jacobgil将在实现的过程中,把模型分为了两个部分,featrues和classifier,这可能和pytorch自带的VGG网络模型格式有关。features和classifier都是sequence格式,主要就是对featrues中各卷积层的filter进行修剪,同时修改下一层连接的卷积层或者全连接层的相应输入。
这里可以基于我的github中的代码来看怎么实现,代码均基于jacobgil的代码进行了一定的修改。总共有四个文件,main.py,prune.py,dataset.py和observe.py。dataset用于导入数据,prune主要是实现剪枝操作,main就是主函数,实现了网络模型搭建、训练、测试、神经元重要性评价等等,最后observe用来对网络训练结果在测试集上的表现进行观察。
源码中,main.py中的class CNN用于建立网络模型。由于prune.py文件的限制,网络最好写成如下形式。features和classifier都是nn.Sequential形式。如果采用其他结构的网络,比如在featrues中嵌套了多个子类nn.Sequential或者在classifier中不适用nn.Linear而是仅采用卷积结构和全局池化层进行分类,则需要对prune.py中的相应部分进行修改。
out = self.features(x)
out = out.view(out.size(0), -1)
out = self.classifier(out)class FilterPrunner主要用于对网络进行剪枝部分的操作。compute_rank函数就是计算网络中各filter的重要性,这之后将重要性低的filter进行记录,最后输出filters_to_prune这个参数作为剪枝的依据。
class PrunningFineTuner_CNN就是整个程序在运行时的主要部分,包含了网络模型的参数配置、训练、测试以及剪枝的调用。在def prune(self)中,我们需要设置每一次循环需要剪枝的数目、最终网络经过剪枝后的filter保留率、每次剪枝之后的fine tune过程的参数等等。我们可以看到调用剪枝过程的核心语句:
model = self.model.cpu()
for layer_index, filter_index in prune_targets:
model = prune_conv_layer(model, layer_index, filter_index)
self.model = model.cuda()这里是将目前的模型,需要剪枝的网络层数以及filter的编号这三个参数输入prune.py中的prune_conv_layer函数,输出经过剪枝之后的网络,循环直到目标filter全部被修剪完毕,最后将修剪完成的模型替换原有的模型。
在prune.py中,我们可以看到,这种修剪实际上是通过重新定义一个卷积层,之后替换原有卷积层来实现的,这也是由于当前框架的一些限制所导致的。注意如果网络中存在非卷积的其他和卷积层输入输出相关联的层如nn.BatchNorm2d等,也需要相应跟随卷积层进行调整。而如果在定义网络的时候嵌套了多个sequence结构,那还得修改main中的部分代码以使得能够定位到子sequence中的卷积层才行。
我个人还是建议大家基于jacobgil的源码,针对自己想要剪枝的神经网络,进行相应的修改,来加深对这种方法的理解。我进行实验时,建立的CNN结构如下:
CNN(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace)
(3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(4): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace)
(6): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(7): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(9): ReLU(inplace)
(10): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(12): ReLU(inplace)
(13): AvgPool2d(kernel_size=2, stride=2, padding=0)
(14): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(16): ReLU(inplace)
(17): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(19): ReLU(inplace)
(20): AvgPool2d(kernel_size=8, stride=8, padding=0)
)
(classifier): Sequential(
(0): Linear(in_features=256, out_features=10, bias=True)
)
)每一批剪枝的数目为32个filter,因为是实验所以这样设置一个恒定参数无妨,但是在实际使用的时候,最好还是将这个参数设置为一个与当前网络总filter成比例的一个数,来使得在剪枝后期网络模型较小的时候,网络一次性失去的filter不至于过多,以避免对正确率造成较大影响。
我们设定的剪枝目标是原始网络filter数目的1/10,就是剪去90%的filter。总共经过25次修剪之后fine tune操作,历代修剪的参数数量如下:
{0: 8, 3: 3, 10: 3, 14: 10, 17: 6, 7: 2}
{14: 8, 17: 14, 7: 4, 0: 1, 10: 5}
{17: 15, 14: 14, 7: 2, 0: 1}
{17: 10, 7: 4, 14: 10, 10: 6, 3: 2}
{10: 4, 14: 13, 7: 7, 17: 6, 3: 1, 0: 1}
{17: 15, 14: 6, 7: 3, 3: 1, 10: 4, 0: 3}
{17: 11, 7: 5, 0: 2, 14: 10, 3: 1, 10: 3}
{14: 12, 17: 12, 3: 2, 7: 3, 10: 3}
{17: 8, 7: 5, 14: 10, 3: 1, 10: 6, 0: 2}
{17: 17, 10: 6, 14: 4, 3: 1, 7: 4}
{17: 12, 7: 7, 14: 9, 10: 2, 0: 2}
{17: 4, 14: 12, 10: 8, 7: 2, 3: 4, 0: 2}
{0: 4, 14: 10, 17: 9, 10: 5, 7: 4}
{17: 11, 14: 14, 10: 2, 3: 2, 7: 3}
{17: 10, 10: 7, 14: 13, 3: 2}
{7: 8, 14: 13, 17: 6, 10: 4, 3: 1}
{14: 8, 17: 9, 10: 5, 7: 7, 3: 2, 0: 1}
{14: 10, 17: 11, 3: 2, 0: 2, 7: 3, 10: 4}
{17: 13, 3: 2, 14: 9, 7: 4, 10: 2, 0: 2}
{7: 10, 17: 8, 14: 6, 3: 2, 10: 5, 0: 1}
{17: 4, 14: 10, 3: 4, 10: 6, 7: 7, 0: 1}
{3: 2, 14: 9, 10: 4, 7: 6, 0: 6, 17: 5}
{7: 3, 14: 11, 10: 8, 17: 6, 3: 4}
{14: 8, 0: 2, 7: 4, 3: 5, 17: 7, 10: 6}
{14: 2, 7: 5, 0: 8, 10: 6, 3: 8, 17: 3}而各代的正确率和与原始网络大小的关系如下图所示,图中横坐标表示剪枝数目占原始网络的百分比,纵坐标:
而从图中可以看出,随着网络剪枝数目的增加,网络的准确率逐步下降,并且下降的越来越快。。。我觉得可能有两个方面的原因:首先是网络本身的容量不足,其次则是固定剪枝数目而导致对最后几代网络造成了不可逆的影响。
不过,为了验证剪枝算法的有效性,我们还是需要建立相应模型模型进行对比,来确定剪枝方法真的能够在拥有相同网络参数的情况下产生更好的效果。这里我们选择网络模型filter保留率为39%的时候(第17次迭代),将剪枝所得结果和重新训练直至收敛的相同模型的结果进行对比。网络结构如下:
CNN(
(classifier): Sequential(
(0): Linear(in_features=81, out_features=10, bias=True)
)
(features): Sequential(
(0): Conv2d(3, 37, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): BatchNorm2d(37, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace)
(3): Conv2d(37, 41, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(4): BatchNorm2d(41, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(5): ReLU(inplace)
(6): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(7): Conv2d(41, 58, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): BatchNorm2d(58, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(9): ReLU(inplace)
(10): Conv2d(58, 55, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): BatchNorm2d(55, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(12): ReLU(inplace)
(13): AvgPool2d(kernel_size=2, stride=2, padding=0)
(14): Conv2d(55, 80, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): BatchNorm2d(80, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(16): ReLU(inplace)
(17): Conv2d(80, 81, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): BatchNorm2d(81, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(19): ReLU(inplace)
(20): AvgPool2d(kernel_size=8, stride=8, padding=0)
)
)对比发现,剪枝所得模型在测试集上的正确率达到了87.07%,而相同模型从头开始训练的话,最终得到的分类正确率为87.05%。两者差别并不大。。。一方面可能是因为网络比较简单,收敛到一个比较好的参数难度不大,但同时也说明此算法还有非常大的优化空间,比如优化剪枝的选择方式(个人觉得可以考虑结合知识蒸馏的某些思想),结合人类的经验对不同层给予不同的剪枝权重等,对于DenseNet这种结构也可以对不同的卷积层进行剪枝,以减少卷积层的冗余等等。