左神算法基础class4—题目3在二叉树中找到一个节点的后继节点、前驱节点

1.题目：在二叉树中找到一个节点的后继节点

现在有一种新的二叉树节点类型如下：
public class Node
{
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int data) { this.value = data; }
}
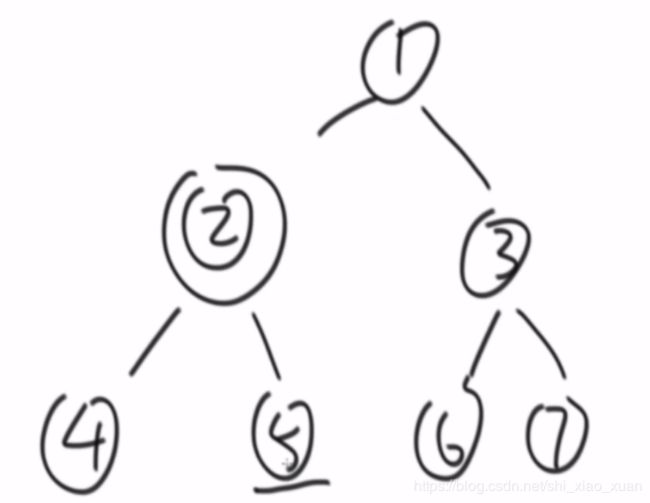
该结构比普通二叉树节点结构多了一个指向父节点的parent指针。假设有一 棵Node类型的节点组成的二叉树，树中每个节点的parent指针都正确地指向自己的父节点，头节点的parent指向NULL。只给一个在二叉树中的某个节点 node，请实现返回node的后继节点的函数。在二叉树的中序遍历的序列中， node的下一个节点叫作node的后继节点。在二叉树中找到一个节点的后继节点。（4,2,5,1,6,3,7是中序遍历的顺序，2是4的中继，5是2的中继。。。后一个数是前一个数的中继节点）

2.分析

本题本质是找中序遍历中一个节点的下一个节点为后继节点。中序遍历的顺序是左中右。
（1）对于一个节点，如果它有右子树，那么这个节点的后继结点就是其右子树的最左节点。原因是中序遍历是左中右的顺序，有右子树，那么节点是中节点，它的下一个节点是右子树中的节点，右子树又是以左中右的顺序，该查找最左的节点。所以当前节点的后继节点是其右子树的最左节点。1的右子树最左节点是6，所以1的中继是6。
（2）对于一个节点如果不存在右子树，那么如果当前节点的父节点的左子树是当前节点，那么其父节点就是当前节点的后继节点。如果不存在，当前节点变为其父节点，继续查找。原因是把父节点视为中节点，如果中节点是后继节点，必须前一个节点是左子树的最后一个节点。对于2,4是2的左子树最后的节点，所以2是4的中继节点，对于1,5也是1左子树最后节点，1是5的中继节点。
（2）情况下若父节点为空时则没有后继节点，7是最后一个节点，没有中继节点。这个边界条件需要注意。

3.核心代码

（1）新二叉树的数据结构

class Tree
{
public:
	int val;
	Tree *right;
	Tree *left;
	Tree *parent;
	Tree(int x)
	{
		this->val = x;
		this->left = NULL;
		this->right = NULL;
		this->parent = NULL;
	}
};

（2）添加树中的节点（由构造函数）

	Tree *head = new Tree(1);
	head->left = new Tree(2);
	head->left->parent = head;
	head->left->left = new Tree(4);
	head->left->left->parent = head->left;
	head->left->right = new Tree(5);
	head->left->right->parent = head->left;

	head->right = new Tree(3);
	head->right->parent = head;
	head->right->left = new Tree(6);
	head->right->left->parent = head->right;
	head->right->right = new Tree(7);
	head->right->right->parent = head->right;

（3）查找后继节点

Tree* getSuccessorNode(Tree *cur)
{
	//节点为空中继节点为空
	if(cur == NULL)
		return cur;
	//右子树存在
	if(cur->right != NULL)
	{
		cur = cur->right;
		while(cur->left!=NULL)//找右子树上最左节点
		{
			cur = cur->left;
		}
		return cur;
	}
	else//右子树不存在
	{
		//父节点为空时没有中继节点；父节点的左子树是当前节点则为中继节点
		while(cur->parent!=NULL && cur->parent->left != cur)
		{
			cur = cur->parent;
		}
		return cur->parent;
	}
}

4.完整代码

#include 
using namespace std;

class Tree
{
public:
	int val;
	Tree *right;
	Tree *left;
	Tree *parent;
	Tree(int x)
	{
		this->val = x;
		this->left = NULL;
		this->right = NULL;
		this->parent = NULL;
	}
};

Tree* getSuccessorNode(Tree *cur)
{
	//节点为空中继节点为空
	if(cur == NULL)
		return cur;
	//右子树存在
	if(cur->right != NULL)
	{
		cur = cur->right;
		while(cur->left!=NULL)//找右子树上最左节点
		{
			cur = cur->left;
		}
		return cur;
	}
	else//右子树不存在
	{
		//父节点为空时没有中继节点；父节点的左子树是当前节点则为中继节点
		while(cur->parent!=NULL && cur->parent->left != cur)
		{
			cur = cur->parent;
		}
		return cur->parent;
	}
}

int main()
{
	Tree *head = new Tree(1);
	head->left = new Tree(2);
	head->left->parent = head;
	head->left->left = new Tree(4);
	head->left->left->parent = head->left;
	head->left->right = new Tree(5);
	head->left->right->parent = head->left;

	head->right = new Tree(3);
	head->right->parent = head;
	head->right->left = new Tree(6);
	head->right->left->parent = head->right;
	head->right->right = new Tree(7);
	head->right->right->parent = head->right;
	//打印
	Tree* succ = getSuccessorNode(head->right);
	if(succ == NULL)
		cout<<"NULL";
	else
		cout<<succ->val;
		
	system("pause");
	return 0;
}

5.补充：查找前驱节点

同理：（1）有左子树时，左子树的最右节点是当前节点的前驱节点。原因是有子树时，当前节点视为中节点，左子树的最右节点是中序遍历中，左中右顺序里左的最后一个节点，下一个节点是中节点即当前节点，所以左子树的最右节点是当前节点前驱节点
（2）当前节点是其父节点的右孩子时，父节点是当前节点的前驱节点。父节点视为中节点,左中右顺序里的中，右孩子是左中右顺序里的右，那么父节点是当前节点的前驱节点。