麦克风阵列波束形成

我的书：

淘宝购买链接
当当购买链接
京东购买链接

#波束形成
beamforming 体现的是声源信号的空域选择性，许多传统波束形成方法具有线性处理结构；波束形成需要考虑三个方面：
1.麦克风阵列个数；2.性能； 3.鲁棒性
在麦克风较少时，波束形成的空域选择性差，当麦克风数量较多时，其波束3dB带宽较为窄，如果估计的目标声源方向有稍有偏差，带来的影响也更大，鲁棒性不好。通常鲁棒性和性能是对矛盾体，需要均衡来看。
通常波束方向图需要随环境的语音/噪声/干扰等统计信息进行调整，以达到最优滤波。常见波束形成的准则如最大信噪比准则（maximum signal-to-noise ratio MSNR），最小均方误差（minimum mean-squared error， MMSE）， 线性约束最小方差（linearly constrained minimum variance， LCMV）。
多通道维纳滤波波束形成使用了最小均方误差MSE准则，
波束形成方法使用信号统计特征（一阶，二阶…），信号和噪声的统计特性通常又是变化的，如人走动，屋内物品移动，外界噪声源变动等，这就需要使用短时平稳和自适应方法来进行波束形成。

webrtc使用了如下几个点以提高鲁棒性和性能（其算法性能优先）：
1.可以使用多个后置滤波器而非一个，2.每个后置滤波使用新的结构。
每个后置滤波器为每个声学场景的时频域bin在均方误意义上提供了最优实增益。在webrtc中后置滤波器根据声源的空域协方差矩阵，干扰源协方差矩阵，绕射场（零阶贝塞尔函数计算）以及临近麦克风的时频信号信息求得。
这样的话就可以为每个声源和干扰场景计算出不同的最优后置滤波器，也可以使用级联的方式灵活使用多个不同选择性的后置滤波器。
当前现存的波束形成算法的鲁棒性成为它们使用的一道门槛，如MVDR和多通道维纳滤波。
webrtc为了增强鲁棒性，在求最优矩阵时，对声源信号添加了限制条件，使用Gabor frame将声源变成时频bin的系数，对这些bin按照目标声源和干扰声源附加了条件，如果满足条件，则门操作让目标声源通过，而让干扰源乘以零以实现选择最优目标信号。
在webrtc中这些增益系数称为自适应标量（上面的实）乘法增益，均方误差准则被用来做为计算的准则。由于阵列方向响应随频率是变换的，而语音信号又是宽带信号，所以webrtc中使用了gabor变换来表示声音信号。增益源于目标信号和干扰的比例。
波动方程常有波数这个参数，相位的信息是通过实部和虚部表示出来的，列两个重要的参数。
##声场
对于中高音，声音在室内以反射和散射为主，这一过程不断重复和往复直到能量变成零（吸收和传输损耗），这一过程约有16次之多。对于低音室内更像一个谐振腔，波长满足谐振条件的声波将会被放大，随着说话位置的位置变化，增强和对消的低音频率也会变化。

Schroeder frequency：
室内声音的谐振腔频率和反射/散射频率的分界点。对于居家室内场景该频率一般在100Hz～200Hz之间，在室内播放一个谐振频率的声波，人在室内不同的位置听到的音量差异是比较明显的，而对于中高音差别并不明显。
散射噪声场：
散射噪声场中，噪声能量向各个方向传播的概率是相等的。
包含若干个来自方向上均匀分布的相位随机的平面波，

假设空间中任意一点的声波压强表达式如下：
$$p(t,r_1)=\underset{n\to \infty }{\lim }\frac{1}{\sqrt{n}}\sum _{i=1}^n{A}_{i}cos(\omega +{\phi }_i)\text{\hspace{1em}(1.0)}$$
$r_1$位置向量，参考点可以任意选取，则另外一点的声压表达时如下：
$$p(t,r_2)=\underset{n\to \infty }{\lim }\frac{1}{\sqrt{n}}\sum _{i=1}^n{A}_{i}cos(\omega +{\phi }_i+(r_2-r_1)\cdot k_i)\text{\hspace{1em}(1.1)}$$
其中$k_1,k_2,k_3,...$是平面波的波数向量。

##相干和非相干噪声
相干噪声

横轴是归一化频率（f=2）

非相干噪声

###波动方程

• 波数（k）
  沿着波的传播方向单位长度内波的全周期数。$k=1/波长=\frac{f}{c}$,也可定义成$k=2\pi /波长$，这样可以理解成相位随距离的变化率。

• 空域混叠
  对于时域有奈奎斯特定理KaTeX parse error: \tag works only in display equations
  在空间上，类似：
  $$f_{x_a}=\frac{1}{d}\ge 2f_{xmax}$$
  在波数方向图上，就是麦克风阵列旁瓣幅度可能大于主瓣幅度。

###近场和远场

远场模型可以看成是平面波（左），传播方向是${\zeta }^0$，远场要看成是球面波（右）,传播方向${\zeta }_m^0$

由于1.麦克风阵列间距相对于说话人距离$1.5m/2.5cm \approx 60
$倍，假设符合远场模型。

固定波束形成

滤波器权值固定，方法简单，运算量低，能够抑制背景噪声，对可变噪声场，效果一般。
###delay-sum
算是最简单的波束形成方法，一般用在电话会议场景，对非相干噪声效果较好，如空间白噪声，然而，如果噪声源是相干的，降噪的程度依赖于噪声的方向，在室内混响场景下，并不能获得很好的效果。
设输入信号是$s(t)$，叠加噪声是加性的$n(t)$，则第m个麦克风观测到的信号是：
$x_m(t)=s(t)+n_m(t)$

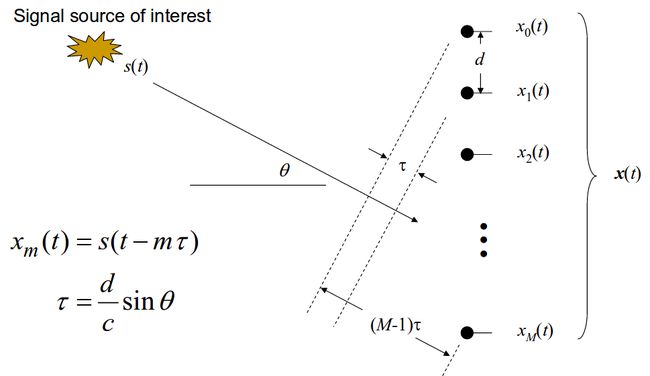
则将每一路信号经过冲击响应延迟后再相加可以得到时间匹配上的信号。

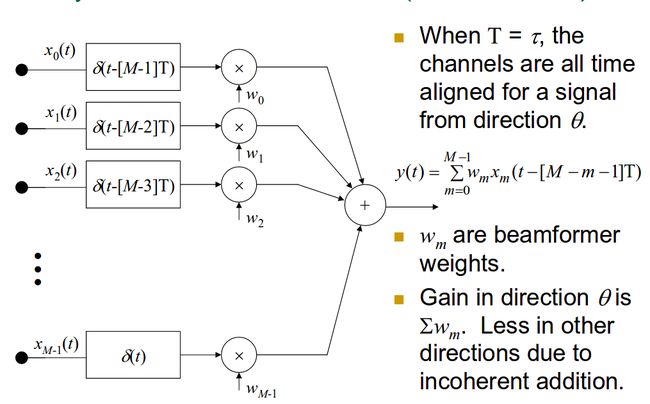
则延迟和输出是：
$y(t)=\sum _{m=0}^{M-1}{w}_m{x}_m(t-[M-m-1]T)$

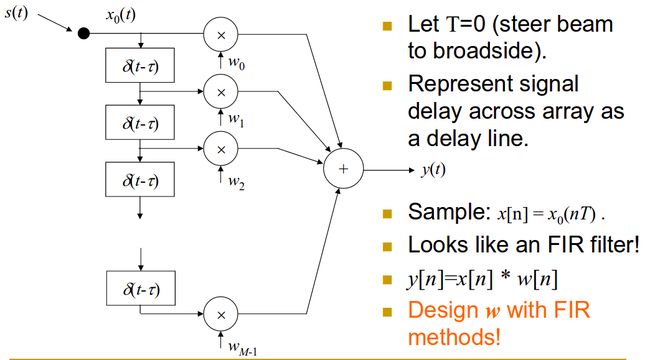
###filter-and-sum

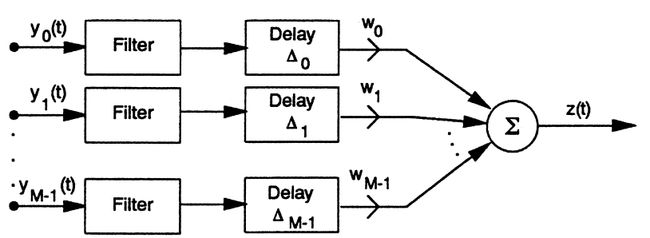
和delay-sum相比其使用了幅度和相位不一致的权重。

##自适应波束形成
如Frost/mvdr等，在相干噪声场，可以得到较高的信噪比改善，但是在弱相干噪声场和在散射噪声场中，性能不如固定波束形成。其一种结构可以如下：

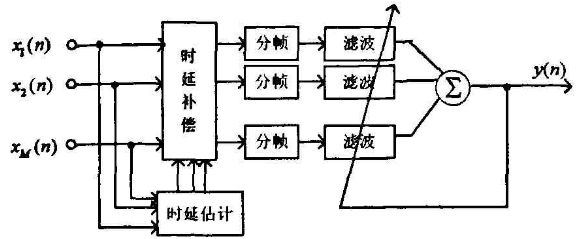
###后置滤波作用
可以用来去除非相干噪声，但是在相干噪声情况下性能退化，甚至不可用。zelinski后置滤波器的结构体如下：

apab(adaptive post-filter for an arbitrary beamformer） 后置滤波器

通常将自适应滤波器和后置滤波器结合起来以抑制相干和非相干噪声。

一张频谱图，可以反映它们之间的对比关系

问题建模如下：
$$z_m(t)=a_m(t)\ast s(t)+n_m(t)=a_m(t)\ast s(t)+n_m^s(t)+n_m^t(t)\text{\hspace{1em}(2.1)}$$
其中m是麦克风索引下标，$n_m^s和n_m^t$分别是稳态和非稳态噪声，$\ast$是卷积,a是传播通道响应。
通过STFT可以得到：
$$Z_m(k,l)=A_m(k)S(k,l)+N_m(k,l)=A_m(k)S(k,l)+N_m^s(k,l)+N_m^t(k,l)\text{\hspace{1em}(2.2)}$$
其中$l$是帧索引，$k=1,2,3,....K$是频率bin索引。对于各个通道合并成向量表示法如下：
$$Z(k,l)=A(k)S(k,l)+N(k,l)+A(k)S(k,l)+N_s(k,l)+N_l(k,l)\text{\hspace{1em}(2.3)}$$
$$Z(k,l)=(Z_1(k,l),Z_2(k,l)...,Z_m(k,l){)}^T$$
当噪声场在空间上是非相干的，仅仅降噪还是不够的，还需要后置滤波，

• 频域Frost算法
  设$W_m^{\ast }(k,l);m=1,2...,M$是M个滤波器，则滤波器组的向量表示如下：
  $$W^H(k,l)=\left[\begin{array}{cccc}{W}_1^{\ast }(k,l)& W_2^{\ast }(k,l)& ...& W_M^{\ast }(k,l)\end{array}\right]\text{\hspace{1em}(2.4)}$$
  
  则滤波求和的输出如下： $$\begin{gathered} Y(k,l)=W^H(k,l)Z(k,l)= \\ {W}^H(k,l)A(k,l)S(k,l)+W^H(k,l)N_s(k,l)+W^H(k,l)N_t(k,l)\triangleq Y_s(k,l)+Y_n,s(k,l)+Y_n,t(k,l)\text{\hspace{1em}(2.5)} \end{gathered}$$
  其中$Y_s(k,l)$是信号部分，而$Y_n,s(k,l)和Y_n,t(k,l)$分别是准平稳噪声和非平稳噪声。波束形成器的输出功率是：
  $$E[Y(k,l)Y^{\ast }(k,l)]=E[W^H(k,l)Z(k,l)Z^H(k,l)W(k,l)]=W^H(k,l){\Phi }_{ZZ}(k,l)W(k,l)\text{\hspace{1em}(2.6)}$$
  ${\Phi }_{ZZ}$是信号的功率谱密度矩阵，目标是$Y_s(k,l)$满足下述约束下输出功率最小：
  $$Y_s(k,l)=W^H(k,l)A(k)S(k,l)={\mathcal{F}}^{\ast }(k,l)S(k,l)\text{\hspace{1em}(2.7)}$$
  $\mathcal{F}$通常是一些前置滤波器，最简单的就是delay-sum中的delay，不失一般性，可以令 $\mathcal{F}=1$则最小化问题可以变为：
  $$\underset{W}{\min }\{W^H(k,l){\Phi }_{ZZ}(k,l)W(k,l)\},W^H(k,l)A(k)=1\text{\hspace{1em}(2.8)}$$
  式2.8一般拉格朗日法进行求解。
  $$\mathcal{L}(W)=W^H(k,l){\Phi }_{ZZ}(k,l)W(k,l)+\lambda [W^H(k,l)A(k)-1]+{\lambda }^{\ast }[A^H(k,l)W(k)-1]\text{\hspace{1em}(2.9)}$$
  其中$\lambda$是拉格朗日乘子，对权重因子$W^{\ast }$求偏导数并令结果等于零，可以得到：
  $${\nabla }_{W^{\ast }}\mathcal{L}W{\Phi }_{ZZ}(k,l)W(k,l)+\lambda A(k)=0\text{\hspace{1em}(2.10)}$$
  再将限制条件代入2.10得到；
  $$W^{LVCM}(k,l)=\frac{{\Phi }_{ZZ}^{-1}A(k)}{A^H(k){\Phi }_{ZZ}^{-1}(k,l)A(k)}\text{\hspace{1em}(2.11)}$$

最小方差（Capon）波束形成

特征向量法（Eigenvector），

GSC/TF-GSC（Transfer function GSC）

GSC包括三个部分：1.固定波束形成，用于对齐延迟后的信号；2.阻塞矩阵（block matrix），用于阻止期望的语音信号，3.自适应噪声相消器，用于滤除固定波束形成旁瓣中残余的噪声。
GSC方法解决的问题和LCMV是一样的，但是把权重向量$W^{LVCM}$分成了两个正交子空间的操作.
$$W^{}$$

SVD

在降维，推荐系统等，信号盲源分离中用。

NTT

方法复杂，但是和传统MVDR相比计算量并没特别大的增加。

线性预测法

###LVCM（又称Frost Filter）
相比维纳滤波，有时无法获得参考信号，这时就无法求得参考信号和观察信号的误差，进而其推导依据的误差是无法获得的，也就无法求解。
维纳滤波的MSE准则的代价函数是：
$$J(\mathbf{h})=E[e(k{)}^2]={\mathbf{h}}^T{\mathbf{R}}_{\mathbf{y}\mathbf{y}}\mathbf{h}-2{\mathbf{r}}_{yx}^T\mathbf{h}+{\sigma }_x^2\text{\hspace{1em}(2.12)}$$
LVCM的思想是既然$x(k)$是无法预知的，那么就令$x(k)=0$，这样把代价函数简化为：
$$J(\mathbf{h})=E[e(k{)}^2]={\mathbf{h}}^T{\mathbf{R}}_{\mathbf{y}\mathbf{y}}\mathbf{h}\text{\hspace{1em}(2.13)}$$
这样的化，就优解将是$\mathbf{h}=0_{L\times 1}$，这样显然不满足要求，可以根据实际问题对$\mathbf{h}$加约束条件：
$${\mathbf{C}}^T\mathbf{h}=\mathbf{u}\text{\hspace{1em}(2.14)}$$
其中$\mathbf{C}$是$L\times L_c$大小约束矩阵，$[u_0]$
$$\mathbf{u}={\left[\begin{array}{cccc}{u}_0& u_1& \cdots & u_{L_c-1}\end{array}\right]}^T$$
则最优滤波器可以表述如下：
$$\underset{\mathbf{h}}{\min }J(\mathbf{h})，约束条件{\mathbf{C}}^T\mathbf{h}=\mathbf{u}\text{\hspace{1em}(2.15)}$$
使用拉格朗日乘子法，可以获得2.11的解。
###MVDR
为了鲁棒性，通常加对角阵扩大主瓣。
###SDW-MWF
speech distortion weighted multichannel winner filter.

上述beamforming算法通常还会加后处理，以减小语音失真度。

###卡尔曼滤波
卡尔曼滤波是维纳滤波的推广，可以处理非稳态过程。
假设观测到的信号是
$$y(k)=x(k)+v(k)={\mathbf{h}}_1^T\mathbf{X}(k)+v(k)\text{\hspace{1em}(3.1)}$$
$v(k)$是零均值高斯白噪声，噪声的方差${\sigma }_v^2=E[v^2(k)]可以随着时间变化，$${\mathbf{h}}_1={\left[\begin{array}{cccc}1& 0& \cdots & 0\end{array}\right]}^T$，假设语音信号可以表示成下式：
$$x(k)=\sum _{l=1}^L{a}_{l}x(k-l)+v(k)\text{\hspace{1em}(3.2)}$$
$a_l,l=1,2,\cdots ,L$可以看成是信号$x(k)$的预测系数，则3.2的向量表示是：
$$\mathbf{X}(k)=\mathbf{A}\mathbf{x}(k-l)+v_x(k){\mathbf{h}}_1\text{\hspace{1em}(3.3)}$$
##BSS（Blind source separation）
使用ICA（independent component analysis）技术。

##CASA（computational Auditory Scene Analysis）
模拟人类听觉系统的分辨能力。