论文解读：手机拍照暗光成像

Handheld Mobile Photography in Very Low Light

在手机拍照中，暗光拍摄是一个非常有挑战的应用场景，受限于手机的硬件配置，没有单反的大镜头，没有单反的大 sensor，所以相对单反来说，手机的硬件配置显得有点先天不足，但是硬件不足，算法来凑，计算摄影，在手机拍照领域，已经越来越受到重视，谷歌更加是这个方向的领先者，这几年，谷歌的计算摄影团队在 ACM Siggraph 上总是会公开一些自家的计算摄影技术，前几代手机，谷歌还是单镜头的配置，在多镜头已经成为趋势的安卓阵营，这种配置显得有点单薄，但是正因为如此，反而倒逼谷歌团队将算法的探索发挥到极致，总会有一些特性给大家带来惊喜，从 HDR，单目虚化，多帧 SR, 到 Low light, 总是会有算法上的创新。

今天介绍的这篇文章是 2019 年 Siggraph 上的一篇文章，主要就是解决手机拍照中的暗光拍摄问题，暗光拍摄，最大的挑战就是噪声和运动模糊，以及颜色的准确性，文章也提到，暗光拍摄中，为了得到一张曝光理想的图像，主要从以下几个角度考虑：

• 增大光圈，可以增大进光量
• 延长曝光时间，同样是为了增大进光量
• 补光，比如打开闪光灯
• 增大 ISO，提升 sensor 的感光能力，同时用去噪算法做后处理

上面提到的几种策略，都有各自的问题，增大光圈，对手机来说，不太现实，因为硬件的限制，延长曝光时间，可能会导致成像模糊，补光的问题，在于导致最后的图像亮度不均匀，可能离得进的主体比较亮，而背景会显得很暗，最后一个方法，增大 ISO，会导致图像的噪声很严重，后期的降噪算法也无法去除干净。

这篇文章介绍的方法，就是从另外一个思路去解决这个问题，暗光拍摄，本质上还是要增大进光量，但是单帧图像延长曝光时间，就会导致运动模糊，除非有三脚架帮忙稳定，一般的拍摄都是手持，难以避免会有轻微的运动，所以另外一个思路就是多帧曝光，将多帧短曝光图像进行融合，这样可以避免长曝光带来的模糊问题，也能增大场景的进光量，所以这篇文章的主要思路还是多帧融合的方法，那么多帧融合，需要解决曝光设置问题：

• 曝光设置，总的曝光时间是多少，每帧图像的曝光时间是多少

与此同时，暗光下的白平衡估计也是一个难点，为了得到和人眼感知相符合的颜色，需要准确地估计暗光下的白平衡。

总结下来，这篇文章的方法，主要从以下几个角度分别解决暗光成像下的不同问题，多帧融合解决进光量及噪声问题，白平衡估计，解决颜色问题，最后 tone mapping 提升局部对比度和细节。文章主要有四个部分，

• 运动测量，或者说运动估计，在预览阶段，就对场景进行运动估计，这篇文章提到了一种高效的运动估计方法
• 在多帧融合的时候，将区域的运动量作为融合权重进行考虑，运动少的地方，权重高，运动多的地方，权重低
• 暗光下的白平衡算法，针对暗光拍摄，设计了专门的白平衡估计
• 特定的 tone mapping 算法，文章里提到了针对暗光下的特定的 tone mapping 算法

• 图一：算法流程

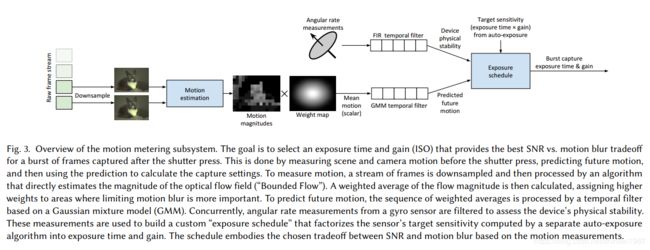
运动测量 motion metering

运动估计，运动测量的目的是为了选择合适的曝光设置，由于手机拍照要求一定的实时性，同时曝光设置一般是基于预览阶段得到，但是最终拍摄和预览阶段可能会有一些不同，所以这个曝光设置需要一定的预见性，需要对实际拍摄时的运动场景有个大致的估计，简单来说，运动测量需要快，准，稳。

• 图 2 运动测量流程

这篇文章用到的运动测量方法，是计算运动量的模值，我们知道，在二维平面上，运动有 x, y 两个方向，所以运动量是一个二维向量场，可以通过取模值，来估计运动量的大小，剩下的问题就是如何快速得到运动量的模值，如果用光流的方法，去计算两帧之间的运动向量场，这个速度估计会很慢，这篇文章利用下面的关系来估计运动量的模值，

$$\Delta I_t(x,y)=g(x,y)v(x,y)$$

$\Delta I_t(x,y)$ 表示像素点 $(x,y)$ 的亮度变化，$g(x,y)$ 表示像素点 $(x,y)$ 的梯度值，$ \vec{v}(x,y) $ 表示运动向量场，一个像素在相邻帧之间的亮度变化，等于该像素的梯度与向量场之间的点积，根据不等式性质：

$$|\Delta I_t(x,y)|\le ||g(x,y)||\cdot ||v(x,y)||$$

所以可以得到：

$$||v(x,y)||\ge \frac{|\Delta I_t(x,y)|}{||g(x,y)||}$$

通过这种方法，可以估计出一个像素点的最低运动量，为了去除暗光区域噪声的干扰，提升运动测量的鲁棒性，文章里面提到把梯度小于一定阈值的都给排除掉：

$$||g(x,y)||\le K\sigma$$

对整个场景计算完运动模值的估计，然后再进行一个加权平均，得到整个场景的一个运动模值，文中也提到，一般是采用中心扩散的方式进行加权平均，简单来说就是中心的权重高，周围的权重低，如果有人脸的话，那就人脸的权重高，如果用户通过交互，选择了某个区域，那么该区域的权重也更高

在预览帧里做完运动测量，剩下的就是运动估计，以使得实际拍摄的时候，可以得到一个比较合理的曝光设置，这是一个时序预测的问题，类似我知道前面 N 帧的运动量 $v_1,v_2,...,v_N$，需要估计后面 K 帧最低的运动量，就类似一个回归预测的问题，这篇文章利用了一个概率模型取实现这个估计：

$$Pr[v_{min}\ge \underset{k=1}{\overset{K}{\min }}{v}_k|v_i,i=1,2,...N]\ge P_{conf}$$

上面这个式子简单来说，就是给定前面 $N$ 帧的运动量估计，我们要预测的 $v_{min}$ 比后面 $K$ 帧里最小的运动量要大，而且这个大的概率要满足一定的阈值，文章里用了 GMM 高斯混合模型来进行建模，

$$1-Pr[v_{min}\le v_k{]}^K\ge P_{conf}$$

$v_k$ 是相对独立的并且是一维的，为了计算 $ Pr[v_{min} \leq v_k] $, 可以利用一维高斯函数来求解。

文章中还考虑相机本身的运动，如果手机是用三脚架固定的，那么可以适当地延长曝光时间，如果手机只是手持，那么曝光时间需要进行限制，这类为了检测手机本身的稳定性，需要借助传感器来实现。

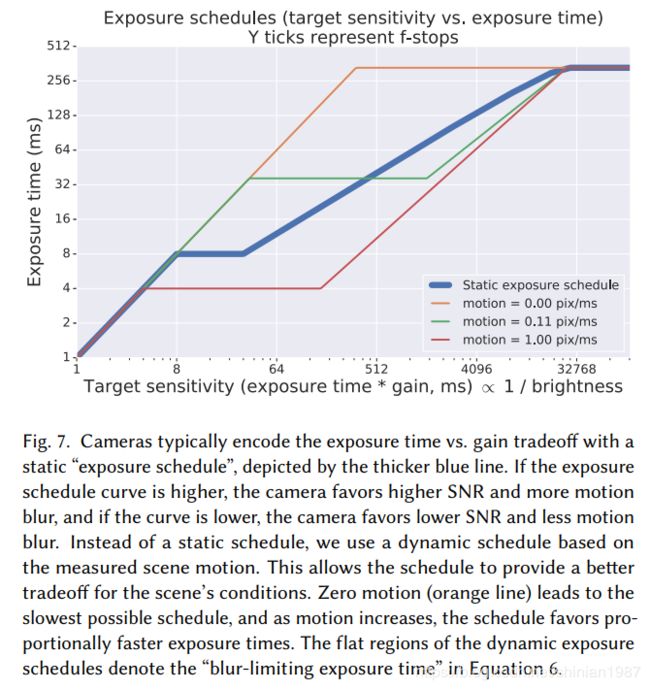
结合运动估计和手机的稳定性估计，最后就要计算曝光设置，文章中提供了一种动态的曝光设置，根据手机的稳定性估计以及运动估计，最终的曝光时间由下式计算：

$$t_{exp}=\frac{B}{v_{min}}$$

• 图三曝光设置

基于运动的自适应多帧融合

前面介绍的是运动测量或者运动估计，这一部分介绍多帧融合，多帧融合是比较常用而且比较有效的一种降噪及融合方案，这部分主要有三个模块，一个是配准对齐，多帧图像一般会有一些偏移，需要选定参考帧，然后其它帧向参考帧对齐，第二个是融合，融合的关键是计算融合权重，第三个是降噪，融合之后再做一个降噪。

文中使用的是块匹配的方式，而融合的时候，利用的是一种 Spatially varying temporal merging 的方法，总体的策略就是融合权重和像素的位置有关，通过比较参考帧和其它帧之间的差异，来决定融合权重。权重是在频域计算的，

$$A_{tz}(w)=\frac{|D_{tz}(w){|}^2}{|D_{tz}(w){|}^2+c{\sigma }_{tz}^2}$$

文章做了进一步的化简，

$$m_{tz}=\frac{d_{tz}^2}{d_{tz}^2+s{\sigma }_{tz}^2}$$

$m_{tz}$ 衡量的是 mismatch 的程度，或者说差异化的程度，$d_{tz}$ 表示的是参考帧与某一帧在某个块上的 $L_1$ 差，最后的权重是：

$$A_{tz}(w)=\frac{|D_{tz}(w){|}^2}{|D_{tz}(w){|}^2+c{f}_{tz}(m_{tz}){\sigma }_{tz}^2}$$

作者指出，这种计算融合权重的方法，比起之前的方法要更鲁棒，而且之前的方法是三个通道分别计算，这个方法是三个通道共用一个权重，直接计算三个通道中的最小值，作者提到，暗光下不同通道的权重差异比较大，如果分开计算容易产生 artifacts

最后就是时序降噪，需要估计融合之后的噪声水平，文章是根据实际融合之后，每个块独立计算噪声水平，然后再进行降噪。

暗光下的 AWB

接下来是暗光下的白平衡估计，因为在光照充足的白天，环境基本都是靠阳光来照亮，所以图像高亮区域的真实亮度是接近白光的，但是夜晚由于人造光源的问题，人造光源很多时候都是五颜六色，而不是白色的，这个就对白平衡的估计造成干扰，我们知道传统的白平衡估计都是寻找白色的点，白色的点，意味着三个通道的亮度值是比较接近的，但是人造光源，有可能造成整张图像偏向某一种颜色，从而导致其它通道的亮度值很低，这篇文章提出了另外一种度量方式，

作者先列出了几种传统的度量方式，

$${\Delta }_l({\mathbf{m}}_p,{\mathbf{m}}_t)=co{s}^{-1}(\frac{{\mathbf{m}}_p^T{\mathbf{m}}_t}{\Vert {\mathbf{m}}_p\Vert \Vert {\mathbf{m}}_t\Vert })$$

其中 $\Vert {\mathbf{m}}_p\Vert$ 表示 RGB 三个通道的估计值，而 \left | \mathbf{m}_t \right | 表示三个通道的实际值，这种方法关注的是还原的亮度值

另外一种方法是考虑预测值和真实值的比值，所以可以得到如下的度量方式：

$${\Delta }_r({\mathbf{m}}_p,{\mathbf{m}}_t)=co{s}^{-1}(\frac{{\Vert \mathbf{r}\Vert }_1}{\sqrt{3}{\Vert \mathbf{r}\Vert }_2}),\mathbf{r}=\frac{\Vert {\mathbf{m}}_t\Vert }{\Vert {\mathbf{m}}_p\Vert }$$

论文给出了一种新的度量方式：

$${\Delta }_a({\mathbf{m}}_p,{\mathbf{m}}_t,{\mathbf{u}}_t)=co{s}^{-1}(\frac{{\sqrt{\mathbf{r}}}^{T}H\sqrt{\mathbf{r}}}{\sqrt{tr(H)}\sqrt{{\mathbf{r}}^{T}H\mathbf{r}}}),H=diag({\mathbf{u}}_t{)}^2$$

${\mathbf{u}}_t$ 表示的是图像的均值，这种方式相比于 ${\Delta }_r$，考虑了真实图像的均值，可以消除某些低亮度通道的干扰，从而可以得到更准确的白平衡估计。

Tone mapping

最后一步就是 tone mapping，tone mapping 简单来说就是一个动态范围压缩，因为我们显示器一般只有 8bit 一个通道，所以需要将高 bit 的 RAW 图，压缩到低比特，同时尽可能保持细节与对比度，作者在文章里估计也尝试了很多不同的方法，最后总结了一个方法，也是一个曲线映射的方法，同时考虑了各种细节，比如分段映射，不同亮度区域，进行饱和度的调整，以及特别暗的地方进行 vignetting 操作，

$$A_s=2.2^{1-\max \left(0,\min (1,\frac{log(E_v)-L_{min}}{L_{max}-L_{min}})\right)}$$

$$A_h=1+0.2\cdot (A_s-1)\cdot (1-D)$$