基于Huffman树的文件压缩原理及C语言实现（一）

什么是二叉树的“带权”路径长度？

设二叉树具有n个带权值的叶子结点，从根结点到各个叶子结点的路径长度与对应叶子结点权值的乘积之和叫做二叉树的“带权”路径长度。

什么是最优二叉树？

对于一组带有确定权植的叶子结点，带权路径长度最小的二叉树称为最优二叉树。

霍夫曼树的几大特点

1. Huffman就是一种最优二叉树。
2. Huffman树肯定最优,不是Huffman树也可能最优树。
3. 只要权值个数(叶结点数)严格大于1，Huffman树中便不存在度为1的结点。
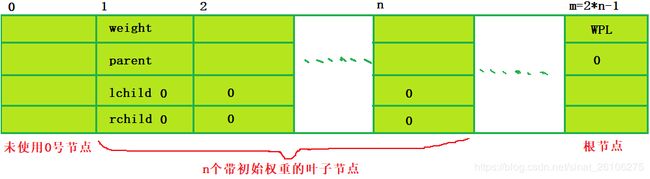
4. 权值个数(叶节点数)为n则Huffman树含2n-1个结点。

霍夫曼树并没有它严格的文字定义，霍夫曼树是构造出来的。
也就是说，要说明一棵树是霍夫曼树，那我们就要根据构造霍夫曼树的方法，能够将其构造出来。

如何构造赫夫曼树—赫夫曼算法

1. 创建n个根结点,权值 {w1,w2,…,wn}, 得森林{T1,T2,…,Tn}；
2. 在森林中选取根结点权值最小的两棵二叉树归并为新二叉树，新二叉树根结点权值为两权值之和；
3. 将新二叉树加入森林，同时忽略被归并的两棵二叉树，
4. 重复（2）和（3，至森林只有一棵二叉树。该二叉树就是哈夫曼树。

赫夫曼树对应的编码称为赫夫曼编码,是一种最优前缀编码。

它的构造比较简单：先建好哈夫曼树，左子树的路径标记为0，右子树的路径标记为1。叶节点的哈夫曼编码就是根节点到叶节点的简单路径上的0、1序列。

霍夫曼树的顺序存储，内存模型如下：

下面给出构建哈夫曼树和哈夫曼编码的c代码：

#include
#include
#include

//函数结果状态代码
#define  TRUE                 1
#define  FALSE                0
#define   OK                  1
#define  ERROR                0
#define  INFEASIBLE           -1
#define  OVERFLOW             -2
typedef  int Status;
typedef unsigned long UInt32;
typedef struct {
	 UInt32 weight;             // 节点权重
	 int parent,lchild,rchild;  // 双亲和左右孩子节点下标
}HTNode,*HuffmanTree,*HTree;

typedef char**HuffmanCode;      //霍夫曼编码类型

/**
 * 从森林中找出两个根结点权重最小的树。
 * 将找到的两棵树的根结点的下标用l和r带回。
 * 入参   T：森林结点数组
 *        n：森林结点数组长度
 */
void Select(HuffmanTree T,int n,int&l,int&r)
{
	//从T的一到n个节点中找出没有结合（即parent=0）的节点中权重weight最小的两个节点的下标；用l，r带回；
	HuffmanTree p=T+1;int a=0,b=0;
	for(int i=1;i<=n;++i,++p){
		if(!p->parent){//找出双亲节点为空的节点；
			if(!a){l=i;a=1;}
			else if(!b){r=i;b=1;}
			else if(p->weight<(T+l)->weight||p->weight<(T+r)->weight){
				if((T+l)->weight<=(T+r)->weight)r=i;
				else l=i;
			}
		}
	}
}

void StrCopy(char*str,const char*c)
{
	char *s=str;
	while(*c!='\0')*s++=*c++;
	*s='\0';
}

/**
 *
 */
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n)
{
	int f,c,start,m1,m2,i,m=2*n-1;HuffmanTree p;
	HT=(HuffmanTree)malloc(sizeof(HTNode)*(m+1));
	if(!HT){printf("内存不足，操作失败！");exit(OVERFLOW);}
	for(p=HT+1,i=1;i<=n;++i,++w,++p){
		p->weight=*w;p->parent=0;p->lchild=0;p->rchild=0;
	}
	for(i=n+1;i<=m;++i,++p){
		p->weight=0;p->parent=0;p->lchild=0;p->rchild=0;
	}
	for(i=n+1,p=HT+i;i<=m;++i,++p){
		Select(HT,i-1,m1,m2);
		p->weight=(HT+m1)->weight+(HT+m2)->weight;
		p->lchild=m1;p->rchild=m2;
		(HT+m1)->parent=i;(HT+m2)->parent=i;
	}

	//for(i=1;i<=m;i++)
	//printf("%d  %d  %d  %d  ",HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild);

	HC=(HuffmanCode)malloc(sizeof(char*)*(n+1));
	if(!HC){
		printf("内存不足，操作失败！");exit(OVERFLOW);
	}
	char *cd=(char*)malloc(sizeof(char)*n);cd[n-1]='\0';
	for(i=1;i<=n;++i){
		start=n-1;
  		for(f=HT[i].parent,c=i; f!=0;c=f,f=HT[f].parent)//叶到根逆向求编码
      		if(HT[f].lchild==c)cd[--start]='0';  else cd[--start]='1';
		HC[i]=(char*)malloc(sizeof(char)*(n-start));
		StrCopy(HC[i],cd+start);
	}
	free(cd);
}

/**
 * 输出霍夫曼编码
 */
void PrintHuffmanCode(HuffmanCode C,int* s,int n)
{
	char *p;
	for(int i=1;i<=n;++i){
	    printf("权重：%3d，编码：", s[i-1]);
		p=C[i];
		while(*p!='\0')
		printf("%c",*p++);
		printf("\n");
	}
}

/**
 * 根据霍夫曼树，将霍夫曼编码后的字符进行解码。
 */
Status Rewin(HuffmanTree &T,char*s,int*x,int n,int &m)
{
	//根据huffman树，将s所指向的字符串解码,要求字符串以#结束。用 x 带回解码在数组中的下标, x 从 1 开始。
	HuffmanTree p=T+2*n-1;m=0;
	 while(*s!='#'){
 		 if(*s=='0'&&p->lchild)p=T+p->lchild;
		 else if(*s=='1'&&p->rchild)p=T+p->rchild;
//		 else return FALSE;
		 if(!p->lchild&&!p->rchild){
 			if(*s=='0')*x=(T+p->parent)->lchild;
 			else *x=(T+p->parent)->rchild;
 			x++;p=T+2*n-1;m++;
 		}
 		s++;
 	}
 	return OK;
}

int main()
{
	int s[20]={7 ,19, 2 ,6 ,32, 3, 21, 10}; // 结点对应得权重
	int x[20],n=8,m;                        // n：叶节点的数目

	HuffmanCode HC;HuffmanTree HT;
	HuffmanCoding(HT,HC,s,n);
	PrintHuffmanCode(HC,s,n);

	printf("\n解码测试\n");
	char*c="0011101110101#";
	if(Rewin(HT,c,x,n,m))//x为每个字符在s中的下标+1；
	printf("编码 %s，解码后对应的权重值如下：\n", c);
	for(int i=0;i<m;i++)
        printf("%4d ",s[x[i]-1]);
}

运行如下：

权重： 7，编码：1100
权重： 19，编码：00
权重： 2，编码：11101
权重： 6，编码：1111
权重： 32，编码：10
权重： 3，编码：11100
权重： 21，编码：01
权重： 10，编码：1101

解码测试
编码 0011101110101#，解码后对应的权重值如下：
19 2 10 21

这样关于建造霍夫曼树，求霍夫曼编码，以及根据霍夫曼编码还原。下一部分在讲文件压缩的实现。