R语言︱机器学习模型评估方案(以随机森林算法为例)
笔者寄语:本文中大多内容来自《数据挖掘之道》,本文为读书笔记。在刚刚接触机器学习的时候,觉得在监督学习之后,做一个混淆矩阵就已经足够,但是完整的机器学习解决方案并不会如此草率。需要完整的评价模型的方式。
常见的应用在监督学习算法中的是计算平均绝对误差(MAE)、平均平方差(MSE)、标准平均方差(NMSE)和均值等,这些指标计算简单、容易理解;而稍微复杂的情况下,更多地考虑的是一些高大上的指标,信息熵、复杂度和基尼值等等。
本篇可以用于情感挖掘中的监督式算法的模型评估,可以与博客对着看:R语言︱监督算法式的情感分析笔记
机器学习算法评估的主要方案为:
机器学习算法的建立——K层交叉检验(数据分折、交叉检验)——计算评价指标——指标深度分析(单因素方差分析、多元正态检验)——可视化(ROG、折线图)
本文以鸢尾花iris数据集+随机森林算法为例进行展示。
——————————————————————————
相关内容:
1、 R语言︱ROC曲线——分类器的性能表现评价
2、机器学习中的过拟合问题
3、R语言︱机器学习模型评估方案(以随机森林算法为例)
——————————————————————————
一、K层交叉检验
k层交叉检验(K-fold cross-validation),CV将原始数据随机分成K组(一般是均分),将其中一个子集做为测试集,其余的K-1组子集作为训练集,以此重复k次,这样会得到K个模型,用这K个模型在k个测试集上的准确率(或其他评价指标)的平均数作为模型的性能评价指标。
比如如果要测试100棵树和150棵树的随机森林模型哪个性能更好?
就需要将两个特定参数的模型通过k层交叉检验,分别构建k次模型,测试k次,然后比较它们的均值、方差等指标。那么问题来了?k值应该为多少呢?我可以不负责任的告诉你,在这方面真的没有银弹(Silver Bullet),除了数据集大小的限制以外,一般来说,k值越小,训练压力越小,模型方差越小而模型的偏差越大,k值越大,训练压力越大,模型方差越大而模型偏差越小,在《The Elements of Statistical Learning》这本书中测试了一些k值,发现k值为10时模型误差趋于稳定。
1、数据打折——数据分组自编译函数
进行交叉检验首先要对数据分组,数据分组要符合随机且平均的原则。
library(plyr)
CVgroup <- function(k, datasize, seed) {
cvlist <- list()
set.seed(seed)
n <- rep(1:k, ceiling(datasize/k))[1:datasize] #将数据分成K份,并生成的完整数据集n
temp <- sample(n, datasize) #把n打乱
x <- 1:k
dataseq <- 1:datasize
cvlist <- lapply(x, function(x) dataseq[temp==x]) #dataseq中随机生成10个随机有序数据列
return(cvlist)
}代码解读:rep这里有点费解,举例k=5,鸢尾花iris数据集有150个样本(datasize=150)的情况下,则为rep(1:5,30)[1:150],比如:1,2,3,4,5...,1,2,3,4,5...(150个)(ceiling为取整函数)。
sample把这150个数字,打乱;
lapply这一句是依次循环执行,相当于for (x in 1:k),dataseq[temp==x],temp==1时,可以从dataseq中随机抽取30(datasize/k=150/5)个数字。
> k <- 5
> datasize <- nrow(iris)
> cvlist <- CVgroup(k = k, datasize = datasize, seed = 1206)
> cvlist
[[1]]
[1] 1 11 13 14 15 16 19 21 23 26 30 33 34 38 39 40 50 60 62 63 75 84 108 120 132
[26] 133 134 135 143 148
[[2]]
[1] 8 12 29 35 36 45 46 52 54 56 66 73 76 82 85 86 95 98 100 102 103 104 123 125 127
[26] 131 136 137 138 140
[[3]]
[1] 3 7 10 17 18 22 25 28 48 55 65 67 70 71 74 78 88 92 93 96 97 99 105 106 111
[26] 121 128 129 130 146
[[4]]
[1] 5 9 27 37 43 49 51 53 58 59 80 83 87 90 101 107 112 113 114 115 116 117 119 122 124
[26] 139 144 145 149 150
[[5]]
[1] 2 4 6 20 24 31 32 41 42 44 47 57 61 64 68 69 72 77 79 81 89 91 94 109 110
[26] 118 126 141 142 147相当于把数据打了5折(每折30个个案),剩下的留着作为训练集。并且生成5份这样的随机数据集。
笔者自问自答:
对于这个K值来说,有两个功能:把数据分成K组;而且生成了K个这样的数据集。但是,为什么打K折,生成的也是K个数据集呢?
答:K折交叉验证中,比如150个案例,分成了5折,则lapply(x, function(x) dataseq[temp==x])中,temp==x不可能出现temp==6的其他数字,所以最多生成了5个list。
做验证的时候,肯定超不过5个数据集。
2、K层交叉验证
一共有23种树数量(j),每种树数量各自分为5折(K,i),每折有30个测试个案的预测值,一共生成3450个数据集。
第一种方法:循环语句写验证
data <- iris
pred <- data.frame() #存储预测结果
library(plyr)
library(randomForest)
m <- seq(60, 500, by = 20) ##如果数据量大尽量间隔大点,间隔过小没有实际意义
for (j in m) { #j指的是随机森林树的数量
progress.bar <- create_progress_bar("text") #的`create_progress_bar`函数创建一个进度条,plyr包中
progress.bar$init(k) #设置上面的任务数,几折就是几个任务
for (i in 1:k) {
train <- data[-cvlist[[i]],] #刚才通过cvgroup生成的函数
test <- data[cvlist[[i]],]
model <- randomForest(Sepal.Length ~ ., data = train, ntree = j) #建模,ntree=J指的树数
prediction <- predict(model, subset(test, select = - Sepal.Length))#预测
randomtree <- rep(j, length(prediction)) #随机森林树的数量
kcross <- rep(i, length(prediction)) #i第几次循环交叉,共K次
temp <- data.frame(cbind(subset(test, select = Sepal.Length), prediction, randomtree, kcross))
#真实值、预测值、随机森林树数、测试组编号捆绑在一起组成新的数据框temp
pred <- rbind(pred, temp) #temp按行和pred合并
print(paste("随机森林:", j))
#循环至树数j的随机森林模型。这样我们就可以根据pred记录的结果进行方差分析等等,进一步研究树数对随机森林准确性及稳定行的影响。
progress.bar$step()
#19行输出进度条,告知完成了这个任务的百分之几
}
}代码解读:j代表随机森林算法的树的数量,i代表K折;这段代码可以实现,随机森林每类j棵树(60、80、100、...、500),i折(5折交叉检验)的实际值、预测值。
其中: for (i in 1:k) train <- data[-cvlist[[i]],] test <- data[cvlist[[i]],] 代表着要循环计算K次,第一个数据测试集为cvlist[1]中的30个随机样本。
然后生成这么几个序列:随机森林预测分类序列、随机森林树数量序列、K次循环交叉序列。并cbind在一起。
pred <- rbind(pred, temp)中,pred是之前定义过的,这样在循环中就可以累加结果了。
图1
第二种方法:apply家族——lapply
当测试的循环数较少或单任务耗时较少时,apply家族并不比循环具有效率上的优势,但一旦比赛由百米变成了马拉松,apply家族的优势就展现出来了,这就是所谓的路遥知马力吧。
R语言中循环语句,大多可以改写,因为apply家族功能太强大,参考博客:R语言︱数据分组统计函数族——apply族
data <- iris
library(plyr)
library(randomForest)
k=5
j <- seq(10, 10000, by = 20) #j树的数量
i <- 1:k #K折
i <- rep(i, times = length(j))
j <- rep(j, each = k) #多少折,each多少
x <- cbind(i, j)
cvtest <- function(i, j) {
train <- data[-cvlist[[i]],]
test <- data[cvlist[[i]],]
model <- randomForest(Sepal.Length ~ ., data = train, ntree = j)
prediction <- predict(model, subset(test, select = - Sepal.Length))
temp <- data.frame(cbind(subset(test, select = Sepal.Length), prediction))
}
system.time(pred <- mdply(x, cvtest)) #mdply在plyr包中,运行了881.05秒
#i,j,实际值、预测值代码解读:j和i分别代表树的数量以及K折,lapply先生成了如图1 中randomtree(j)以及kcross(i)序列;
然后写cvtest函数,计算不同的j和i的情况下,预测值、实际值,然后将i和j的值,cbind合并上去。
mdply函数,是在plyr包中的apply家族,可以依次执行自编函数。而普通的apply家族(apply、lapply)大多只能执行一些简单的描述性函数。
——————————————————————————————————————————————————————
二、计算评价指标
主要以平均绝对误差(MAE)、均方差(MSE)、标准化平均绝对方差(NMSE)这三个评价指标为主,其他可见博客:R语言︱机器学习模型评价指标
计算公式为:
三者各有优缺点,就单个模型而言,
虽然平均绝对误差能够获得一个评价值,但是你并不知道这个值代表模型拟合是优还是劣,只有通过对比才能达到效果;
均方差也有同样的毛病,而且均方差由于进行了平方,所得值的单位和原预测值不统一了,比如观测值的单位为米,均方差的单位就变成了平方米,更加难以比较;
标准化平均方差对均方差进行了标准化改进,通过计算拟评估模型与以均值为基础的模型之间准确性的比率,标准化平均方差取值范围通常为0~1,比率越小,说明模型越优于以均值进行预测的策略,
NMSE的值大于1,意味着模型预测还不如简单地把所有观测值的平均值作为预测值,
但是通过这个指标很难估计预测值和观测值的差距,因为它的单位也和原变量不一样了,综合各个指标的优缺点,我们使用三个指标对模型进行评估。
1、三个指标自编函数
maefun <- function(pred, obs) mean(abs(pred - obs))
msefun <- function(pred, obs) mean((pred - obs)^2)
nmsefun <- function(pred, obs) mean((pred - obs)^2)/mean((mean(obs) - obs)^2)平均绝对误差(MAE)、均方差(MSE)、标准化平均绝对方差(NMSE)三个指标的自编函数。
以便后续应用apply族来进行运算,这样可以避免循环,浪费大多时间。2、三大指标计算
23种树数量方式(j),每一折的汇总mse指标,有5折,共215个案例。
代码中运用了dplyr包,这个包是数据预处理、清洗非常好用的包,升级版plyr包。
library(dplyr)
eval <- pred %>% group_by(randomtree, kcross) %>% #randomtree=j,kcross=i
summarise(mae = maefun(prediction, Sepal.Length),
mse = msefun(prediction, Sepal.Length),
nmse = nmsefun(prediction, Sepal.Length))代码解读:%>%为管道函数,将数据集传递给`group_by`函数——以randomtree,kcross为分组依据(有点像data.table中的dcast,进行分组)进行统计计算。
group_by()与summarise函数有着非常好的配合,先分组生成group_by格式的文件(dplyr包中必须先生成这个格式的文件),然后进行分组计数。
一共125个案例,如下图。
图2
——————————————————————————————————————————————————————
三、深度解析三大指标——方差分析+多元正态检验
检验不同树数的随机森林三个指标是否存在显著的差异,其实就是进行单因子方差分析,在进行方差分析之前首先要检验方差齐性,因为在方差分析的F检验中,是以各个实验组内总体方差齐性为前提的;
方差齐性通过后进行方差分析,如果组间差异显著,再通过多重比较找出哪些组之间存在差异。
以下两个方法的检验,都需要因子型分类数据(这里是树J或折数i,要转化为因子型)。1、单因素方差分析
以检验不同树j,MAE指标为例,
> eval$j <- as.factor(eval$randomtree)
> bartlett.test(mae ~ randomtree, data = eval) #bartlett方法检验指标mae的方差齐性
Bartlett test of homogeneity of variances
data: mae by randomtree
Bartlett's K-squared = 0.18351, df = 22, p-value = 1
> temp <- aov(mae ~ randomtree, data = eval) ##可以选择前100行,方差分析
> summary(temp)
Df Sum Sq Mean Sq F value Pr(>F)
randomtree 1 0.000 0.000000 0 0.997
Residuals 113 0.393 0.003478 解读:第1行首先要将分组变量转化为因子;
2行使用bartlett方法检验指标mae的方差齐性,为什么检验方差齐性,其目的是保证各组的分布一致,如果各组的分布都不一致,比较均值还有什么意义,F越小(p越大,大于P0.05),就证明没有差异,说明方差齐;
`aov`函数对mae指标进行方差分析,
summary显示差异不显著,说明不同树数的随机森林的mae指标差异不显著(p远远大于0.05),即没有必要做多重正态检验了,但为了展示整个分析流程,还是得做一下。
2、多重检验——组间差异检验
> TukeyHSD(temp) #`TukeyHSD`进行多重比较,多元正态检验,同多元分析中的第一章节
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = mae ~ randomtree, data = eval)
$randomtree
diff lwr upr p adj
80-60 6.637802e-03 -0.1473390 0.1606147 1
100-60 2.703008e-03 -0.1512738 0.1566799 1
120-60 6.482599e-03 -0.1474942 0.1604594 1
140-60 3.172459e-03 -0.1508044 0.1571493 1
160-60 7.967802e-03 -0.1460090 0.1619447 1
180-60 2.244064e-03 -0.1517328 0.1562209 1——————————————————————————————————————————————————————
四、可视化——三大指标折线图
统计检验让我们坚信各种树数的随机森林之间的差异不显著,但是很多人总是坚信眼见为实,那我们不妨将三个指标随树数的变化趋势可视化,使用折线图分析一下它们的差异。
本次绘图主要按照三大指标在随机森林树的数量(j)下的差异,所以会暂时把折数i剔除。
1、自备绘图函数——自备添加主副标题的函数
title_with_subtitle = function(title, subtitle = "") {
ggtitle(bquote(atop(.(title), atop(.(subtitle)))))
}2、数据整理
eval <- aggregate(cbind(mae, mse, nmse) ~ randomtree, data = eval, mean)
eval <- melt(eval, id = "randomtree") #行melt函数将数据表从wide型转化为long型,便于ggplot2做图
eval$randomtree <- as.numeric(as.character(eval$randomtree))代码解读:aggregate,剔除非整理变量,折数i,然后计算每组的平均值,三个指标做透视表求取均值;
melt函数将数据表从wide型转化为long型,便于ggplot2做图;
as.num(as.character)用于将原来为整数类型变量转化为因子变量,便于ggplot2按照因子水平分组。
3、可视化
#绘图
library(ggplot2)
library(reshape2)
p <- ggplot(eval, aes(x = randomtree, y = value, color = variable)) +
geom_line(size = 1.3) +
geom_vline(xintercept = 250, color = "#FF1493", size = 1.3) +
facet_wrap(~ variable, nrow = 3, scales = "free") +
scale_color_manual(values = c("#800080", "#FF6347", "#008B8B")) +
#scale_x_continuous(breaks = seq(0, 10000, by = 100)) +
ylab("") +
xlab("随机森林树数") +
title_with_subtitle("随机森林应该有多少棵树", "抗过拟合并非不会过拟合") +
theme_bw(18) + theme(panel.background = element_rect(fill = rgb(red = 242,
green = 242, blue = 242, max = 255)),
plot.background = element_rect(fill = rgb(red = 242,
green = 242, blue = 242, max = 255)),
plot.title = element_text(size = rel(1.2), family = "STXingkai", face = "bold", hjust = 0.5, colour = "#3B3B3B"),
panel.grid.major = element_line(colour=rgb(red = 146, green = 146, blue = 146, max = 255),size=.75),
panel.border = element_rect(colour = rgb(red = 242,
green = 242, blue = 242, max = 255)),
axis.ticks = element_blank(),
axis.text.x = element_text(colour = "grey20", size = 8),
axis.text.y = element_text(colour = "grey20", size = 10),
axis.title.y = element_text(size = 11, colour = rgb(red = 74,green = 69, blue = 42, max = 255), face = "bold", vjust = 0.5),
axis.title.x = element_text(size = 11, colour = rgb(red = 74,green = 69, blue = 42, max = 255), face = "bold", vjust = -0.5),
legend.background = element_rect(fill = rgb(red = 242,green = 242, blue = 242, max = 255)),
legend.position = "")需要加载(ggplot2)、(reshape2)两个包,然后进行绘图。
本文大多学习之《数据挖掘之道》,还未出版,摘录自公众号:大音如霜,感谢老师的辛勤,真的是非常用心的在写代码以及服务大众。
————————————————————————————
延伸一:异常检测算法--Isolation Forest
南大周志华老师在2010年提出一个异常检测算法Isolation Forest,在工业界很实用,算法效果好,时间效率高,能有效处理高维数据和海量数据,这里对这个算法进行简要总结。
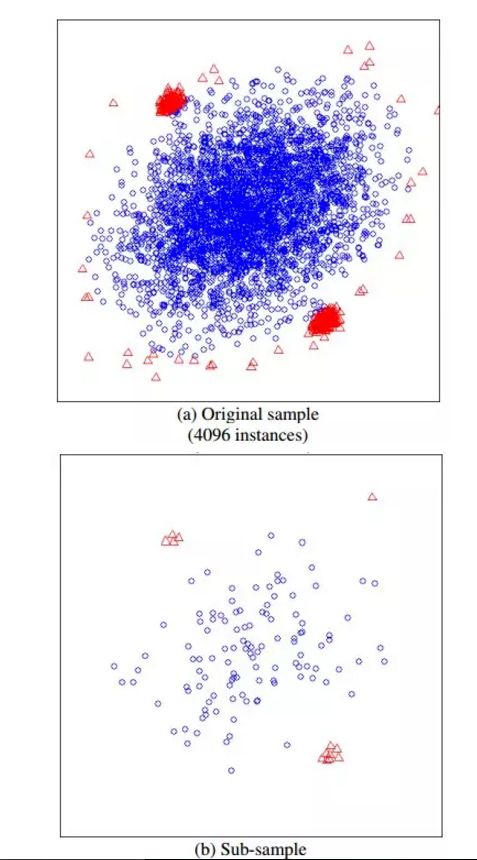
iForest是怎么构造的,给定一个包含n条记录的数据集D,如何构造一个iForest。iForest和Random Forest的方法有些类似,都是随机采样一一部分数据集去构造每一棵树,保证不同树之间的差异性,不过iForest与RF不同,采样的数据量PsiPsi不需要等于n,可以远远小于n,论文中提到采样大小超过256效果就提升不大了,明确越大还会造成计算时间的上的浪费,为什么不像其他算法一样,数据越多效果越好呢,可以看看下面这两个个图,
左边是元素数据,右边是采样了数据,蓝色是正常样本,红色是异常样本。可以看到,在采样之前,正常样本和异常样本出现重叠,因此很难分开,但我们采样之和,异常样本和正常样本可以明显的分开。
除了限制采样大小以外,还要给每棵iTree设置最大高度l=ceiling(logΨ2)l=ceiling(log2Ψ),这是因为异常数据记录都比较少,其路径长度也比较低,而我们也只需要把正常记录和异常记录区分开来,因此只需要关心低于平均高度的部分就好,这样算法效率更高