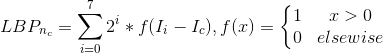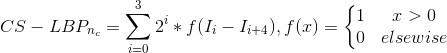图像处理(十一):常用特征三剑客Haar、LBP和HOG
最常用到的三种特征分别为Haar特征、LBP特征及HOG特征,三种特征描述了三种不同的局部信息:
1) Haar描述的是图像在局部范围内像素值明暗变换信息;
2) LBP描述的是图像在局部范围内对应的纹理信息;
3) HOG描述的则是图像在局部范围内对应的形状边缘梯度信息。
三种特征在图像处理和机器学习领域都得到了广泛的应用,在此做一个总结,方便后面复习。
1、Haar特征
最容易接触到Haar特征地方应该就是opencv自带的人脸检测器,所采用的就是Haar特征结合Adaboost算法来实现的,利用Haar特征表征人脸在局部范围内像素值的明暗变化信息,结合积分图技巧加速训练一个级联的Adaboost分类器。Haar特征表示如图1所示。
图1 Haar特征(摘自博客[1])
计算过程就是黑色矩形区域内像素值之和减去白色矩形区域内像素值之和,计算过程其实很简单。但是,直接计算的话,针对每一个矩形区域,我们都需要做一次循环,计算区域内像素之和,对每个位置进行滑窗遍历进行Haar特征提取会使得计算量爆炸,因此,一般Haar特征会配合积分图技术一起来使用。
积分图计算如图2所示,经过计算后,积分图中每个点对应值Inter(x,y)为对应蓝色矩形区域像素值之和。
图2 积分图计算示意图
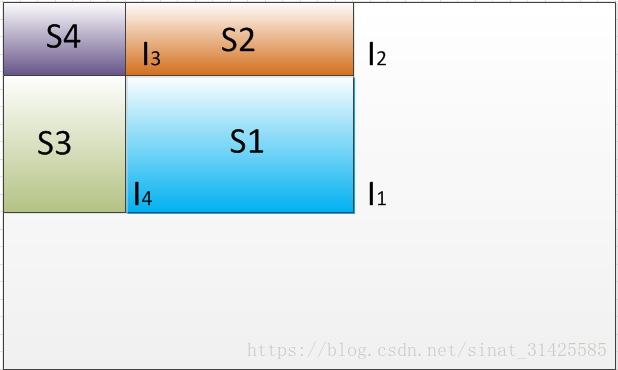
当需要提取Haar特征时,我们需要计算矩形块中像素值之和时,我们只需要将其四个顶点对应于积分图中的值拿出来,做一个求和操作即可,计算过程如图3所示。
图3 利用积分图提取Haar特征原理示意图
图3中S1区域为要提取特征区域,I1,I2,I3,I4分别对应四个顶点位置对应于积分图中的值,由积分图计算过程不难发现:
![]()
![]()
![]()
![]()
因此,![]() ,一个矩形区域内像素累加求和计算转变成了几个值的加减运算,大大的提升了算法执行效率。
,一个矩形区域内像素累加求和计算转变成了几个值的加减运算,大大的提升了算法执行效率。
2、LBP特征
LBP特征对于传统的人脸识别而言,应该是十分有效的。LBP特征提取的思路就是,图像中某一个物体应该包含有多个像素,而且像素与像素之间位置关系应该是连续的,也即是说,在空间位置上有关联的像素信息也是有关联的,因此,可以考虑利用在空间位置上邻近的像素来对当前像素进行二进制编码,这也就是LBP。
常见的LBP有LBP,CS-LBP,Uniform-LBP,圆形LBP和旋转不变LBP等。
2.1 LBP、CS-LBP和Uniform-LBP
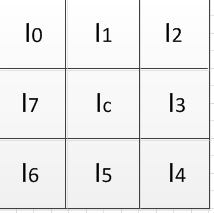
其中,LBP、CS-LBP和Uniform-LBP都是基于当前像素的八邻域来计算的,八邻域示意图如图4所示。
图4 八邻域示意图
LBP计算公式为:
然而原始的LBP存在以下几个问题:
1) 固定邻域内的编码,对于尺度比较敏感,例如,人脸尺寸发生变化,人脸编码会出现误差;
2) LBP特征的维度为![]() 维,特征维度过高;
维,特征维度过高;
3)对于光照、旋转等因素敏感。
针对上述问题,CS-LBP利用中心对称的思想对局部纹理进行描述,其计算公式为:
不难发现CS-LBP特征的维度为![]() 维,相较于传统的LBP,大大地降低了特征维度,大大提升了计算效率。同时,这种对称计算的方式,能够在一定程度上应对光照、旋转等因素。
维,相较于传统的LBP,大大地降低了特征维度,大大提升了计算效率。同时,这种对称计算的方式,能够在一定程度上应对光照、旋转等因素。
Uniform-LBP翻译过来可以是等价模式,作者Ojala的灵感来自于,通过大量实验发现:在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变,因此,在实际应用中,我们只需要统计那些跳变次数在[0,2]之间的二进制模式(这些LBP也称之为等价模式,即Uniform-LBP),经过统计发现,满足这样的LBP总共只有58种,这样,256维的LBP就变成了58维的Uniform-LBP了。
2.2 圆形LBP和旋转不变LBP
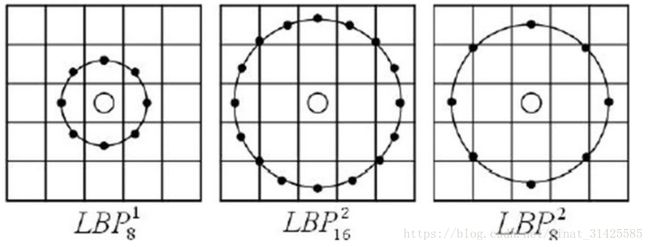
不难发现,无论是LBP、CS-LBP还是Uniform-LBP都是固定邻域内的编码,对于尺度较为敏感,圆形LBP采用圆形邻域取代3方形邻域,并且可以通过调整半径,将3x3大小领域扩展到任意大小邻域,如图5所示。
图5 圆形LBP计算示意图(摘自博客[2])
对于未落在整数位置的点,可以采用双线性插值来获取,圆形LBP可以在一定程度上缓解尺度因素引起的变化,但是对于旋转因素较为敏感,因此,在圆形LBP的基础上,研究者提出了旋转不变LBP。
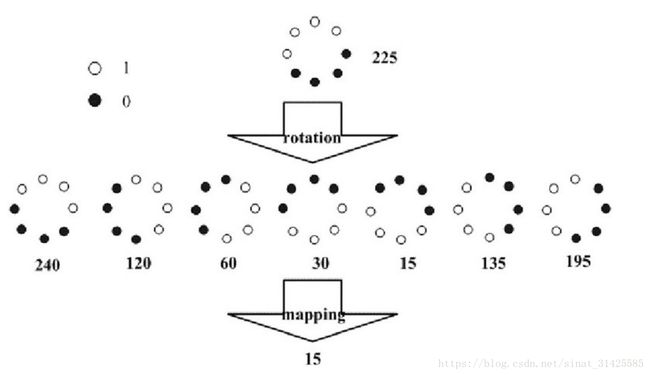
旋转不变LBP对应旋转不变指的是,将圆形领域进行旋转LBP编码,将最小的LBP编码值作为当前像素点的编码值,这样,当物体发生旋转时,能够提取到的LBP编码值具备一定的旋转不变性,旋转不变LBP示意图如图6所示。
图6 旋转不变LBP计算示意图
这里贴一下CS-LBP+Histogram统计的代码:
// (ni - ni+4)* pow(2, i)
Mat CSLBP(const Mat & src, double * lbp_hist, Mat &out)
{
Mat img;
src.copyTo(img);
uchar UTable[16];
// 计算二进制表示,并通过查表的方式,获取其对应的等价模式下的值
for (int i = 1; i < img.rows - 1; i++)
{
for (int j = 1; j < img.cols - 1; j++)
{
uchar code = 0;
for (int m = 0; m < 4; m++)
{
code |= (src.at(i - 1, j - 1) >= src.at(i + 1, j + 1)) << 0;
code |= (src.at(i, j - 1) >= src.at(i, j + 1)) << 1;
code |= (src.at(i + 1, j - 1) >= src.at(i - 1, j + 1)) << 2;
code |= (src.at(i + 1, j) >= src.at(i - 1, j)) << 3;
}
img.at(i, j) = code;
}
}
out = img;
for (int i = 1; i < img.rows - 1; i++)
{
for (int j = 1; j < img.cols - 1; j++)
{
UTable[img.at(i, j)]++;
}
}
// 查找最大值
float max_hist_val = 0;
for (int i = 0; i < 16; i++)
{
if (max_hist_val < UTable[i])
{
max_hist_val = UTable[i];
}
}
//cout << max_hist_val << endl;
for (int i = 0; i < 16; i++)
{
lbp_hist[i] = 1.0 * UTable[i] / max_hist_val;
//cout << "lbp_hist: " << lbp_hist[i] << endl;
}
Mat LBP_hist = Mat::zeros(32, 17 * 2, CV_8U);
Mat LBP_hist_color;
cvtColor(LBP_hist, LBP_hist_color, COLOR_GRAY2BGR);
for (int i = 0; i < 16; i++)
{
//cout << 1 - UTable[i] << endl;
rectangle(LBP_hist_color,
Point(i * 2, 32),
Point((i + 1) * 2, int((1 - lbp_hist[i]) * 32)),
Scalar(255, 0, 0));
}
return LBP_hist_color;
} 其余几种LBP,可以参考博客[4]。
3、HOG特征
HOG特征也是一种被广泛应用的特征,这种特征最早用于行人检测领域。当然,方法都是可以相互借鉴的,在另外一个十分著名的开源库dlib中,人脸检测采用的就是HOG特征训练一个SVM分类器的思路来做的,经过评测,对比opencv的haar特征+Adaboost的做法,HOG+SVM会更加准确,当然,在速度上来说haar+Adaboost会更快。
由于梯度主要对应于图像中的边缘, HOG的基本思路就是统计目标物体的局部形状边缘梯度信息,主要计算步骤如下:
1) gamma变换:降低局部阴影和光照变化影响;
2) 梯度计算:利用一阶或二阶差分近似计算图像梯度及方向
梯度分量计算:
梯度和方向计算:
3) 方向划分:
这个步骤实际上做的就是将方向对应角度区间离散化及模糊处理。首先,将方向对应角度无符号化,其实本质上就是将位于一条直线上的两个方向都视为一个角度,也即是![]() 与
与![]() 视为同一个角度,其中
视为同一个角度,其中![]() ,这样方向范围就变成了
,这样方向范围就变成了![]() ;然后,将角度范围均等划分为9个bins,每一个bin对应一个角度,所有bins对应的角度为:
;然后,将角度范围均等划分为9个bins,每一个bin对应一个角度,所有bins对应的角度为:
![]()
4) 梯度直方图统计:
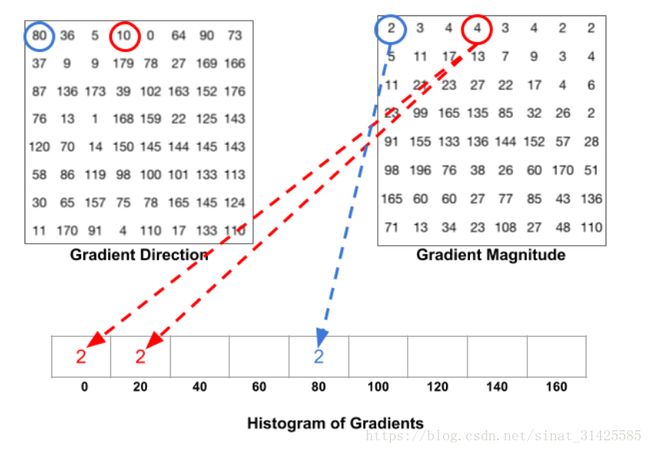
做梯度方向统计时,为什么要考虑对应梯度值?原因很简单,因为实际上,一个像素的梯度值越大,该像素为边缘的可能性越大,在做梯度方向统计时,会考虑到对应梯度值进行加权,然而,加权过程中存在方向位于方向划分的边界上,这个时候就将梯度平均到对应两个区间,计算过程如图7所示。
图7 梯度直方图计算示意图(摘自参考文献[3])
例如,红色虚线对应部分,梯度方向![]() 为
为![]() ,这时就将梯度值4平均划分给0和
,这时就将梯度值4平均划分给0和![]() 对应bin,对应于0度和20度bin各自增加2。如果当前梯度方向
对应bin,对应于0度和20度bin各自增加2。如果当前梯度方向![]() 位于
位于![]() 和
和![]() 之间时,将梯度用插值的方式进行分配统计,统计过程如图8所示。
之间时,将梯度用插值的方式进行分配统计,统计过程如图8所示。
图8 梯度直方图计算方式(摘自参考文献[3])
计算过程如下:
而单个像素的梯度对于噪声比较敏感,直接对每一个像素梯度进行统计,得到的特征可能不够鲁棒,因此,将图像进行分块统计,HOG原文是将图像划分为8x8大小的cell,cell的个数为:
![]()
为进一步降低HOG特征对于噪声、光照等因素的影响,将cell进一步组合,将2x2个cell组合成一个block,然后对block进行归一化处理。组合过程如图9所示。
图9 cell组合成block过程示意图(摘自文献[3])
组合完之后,每个block表示的向量大小为4x9=36,如果图片大小为128x64,那么cell的个数为:128/8x64/8=16x8,对应block个数为:(16-2+1)*(8-2+1)=15x7=105个,因此,最终得到hog特征的维度为36x105=3780维。
~~~~未完待续,后面补充代码及应用。
参考文献:
[1] https://blog.csdn.net/xiaowei_cqu/article/details/8216109
[2] https://blog.csdn.net/kuweicai/article/details/79039218
[3] https://www.learnopencv.com/histogram-of-oriented-gradients/
[4] https://blog.csdn.net/lsq2902101015/article/details/48680779