《Python数据分析与数据挖掘实战》第十三章学习——预测
这一章内容是对财政收入的影响因素进行分析,并构建预测模型。
本章数据比较清楚,几乎不用做清洗工作,主要工作都在模型构建上,中间涉及到的算法有Lasso算法的改进算法——Adaptive-Lasso、书中自己编写的灰色预测、神经网络。
书中对财政地方收入、增值税、营业税、政府基金收入等都做了预测,但每一个预测所用模型和构建过程都类似,因此本文只选择财政地方收入作为例子进行整理。
本文主要分为以下几个部分:
- 探索性分析
- 灰色预测
- 神经网络
- 总结
探索性分析
对变量进行描述性分析和相关性分析。
代码如下:
#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
inputfile='D:/ProgramData/datapath.csv'
data = pd.read_csv(inputfile) #读取数据
#描述分析
r = [data.min(), data.max(), data.mean(), data.std()] #依次计算最小值、最大值、均值、标准差
r = pd.DataFrame(r, index = ['Min', 'Max', 'Mean', 'STD']).T #表格化
r=np.round(r, 2) #保留两位小数
#相关性分析
r_c=np.round(data.corr(method = 'pearson'), 2) #计算相关系数矩阵,保留两位小数查看r_c中各变量与y(即财政收入)的相关性,结果如下:
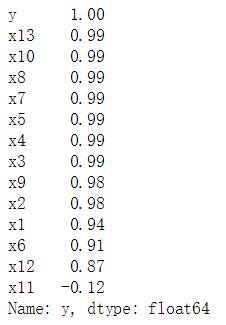
可见除了X11(居民消费价格指数),其余变量均与财政收入呈现高度正相关。
灰色预测
书中在构建预测模型之前利用了Adaptive-Lasso进行变量选择,但现在python的sklearn包里已经没有这个算法,找了很久也没找到这个函数,其他的替代函数也没有找到,此处就不做这个变量选择了,直接参考书上的变量选择结果,进行预测模型构建。
灰色预测原理可参照[灰色预测模型]。(https://wenku.baidu.com/view/0abf24b7a5e9856a57126015.html)
书中所给灰色预测函数基本是按照其原理一步步完成的计算推导,具体代码如下:
def GM11(x0): #自定义灰色预测函数
import numpy as np
x1 = x0.cumsum() #1-AGO序列
z1 = (x1[:len(x1)-1] + x1[1:])/2.0 #紧邻均值(MEAN)生成序列
z1 = z1.reshape((len(z1),1))
B = np.append(-z1, np.ones_like(z1), axis = 1)
Yn = x0[1:].reshape((len(x0)-1, 1))
[[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数(最小二乘法估计参数)
f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值
delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)]))
C = delta.std()/x0.std()
P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0)
return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率灰色预测是利用时间序列预测,主要用于对2014年和2015年的几个变量进行预测,比如这里的x1,x2,x3,x4,x5,x7,为后面的神经网络预测提供变量。
导入函数,对财政地方收入进行预测。
代码如下:
#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import sys
#添加自定义函数所在位置
sys.path.append('D:/ProgramData/codepath')
#前一个GM11为文件名,后一个为函数名
from GM11 import GM11
inputfile='D:/ProgramData/PythonDataAnalysiscode/chapter13/demo/data/data1.csv'#定义输入数据路径
outputfile='D:/ProgramData/PythonDataAnalysiscode/chapter13/demo/outdata/data1_GM11.xls'#定义输出数据保存路径
data=pd.read_csv(inputfile)
data.index=np.arange(1994,2014)
data.loc[2014]=None
data.loc[2015]=None
l=['x1','x2','x3','x4','x5','x7']#根据变量选择选取这六个变量
for i in l:
f = GM11(data[i][np.arange(1994, 2014)].as_matrix())[0]#灰色预测函数
data[i][2014] = f(len(data)-1) #2014年预测结果
data[i][2015] = f(len(data)) #2015年预测结果
data[i] = data[i].round(2) #保留两位小数
data[l+['y']].to_excel(outputfile) #结果输出 需要注意的是,python2.7和python3.5中的range()有区别,前者表示list,而后者表示迭代器,因此上述代码不能使用range,会报错,改成numpy里的arange。
变量填充结果如下图:
![]()
所需变量都已经填充上了,接下来要对财政地方收入,也就是y进行预测。
神经网络
关于神经网络的python程序包下载、后端设置都已经在第六章的时候说过了,其实现在用了python3.5之后,再用神经网络就直接用默认的tensorflow后端就好了,很方便。
以灰色模型预测结果中的变量为特征变量,以y为预测值,构建神经网络模型,并画出准确值与预测值的分布图。
代码如下:
#-*- coding: utf-8 -*-
import numpy as np
import pandas as pd
inputfile='D:/ProgramData/PythonDataAnalysiscode/chapter13/demo/outdata/data1_GM11.xls'
outputfile='D:/ProgramData/PythonDataAnalysiscode/chapter13/demo/outdata/revenue.xls'
modelfile='D:/ProgramData/PythonDataAnalysiscode/chapter13/demo/outdata/1-net.model'
data=pd.read_excel(inputfile)
feature=['x1','x2','x3','x4','x5','x7']#特征所在列
data_train=data.loc[np.arange(1994,2014)].copy()
data_mean=data_train.mean()
data_std=data_train.std()
#零均值标准化
data_train=(data_train-data_mean)/data_std
x_train=data_train[feature].as_matrix()
y_train=data_train['y'].as_matrix()
from keras.models import Sequential
from keras.layers.core import Dense,Activation
from keras.callbacks import EarlyStopping
early_stopping = EarlyStopping(monitor='loss', patience=5)#提早停止
model.add(Dense(12,input_dim=6,init='uniform'))#输入层6层,隐藏层12层
model.add(Activation('relu'))#激活函数为relu,能够大幅度提高准确度
model.add(Dense(1,input_dim=12))#隐藏层12层,输出层1层
model.compile(loss='mean_squared_error',optimizer='adam')#编译模型
model.fit(x_train,y_train,nb_epoch=10000,batch_size=16,callbacks=[early_stopping])#训练模型,学习一万次,如果误差不再减少,就提早停止
model.save_weights(modelfile)#保存模型参数
#预测,并还原结果
x=((data[feature]-data_mean[feature])/data_std[feature]).as_matrix()
data[u'y_pred']=model.predict(x)*data_std['y']+data_mean['y']
data.to_excel(outputfile)
#画出预测结果图
import matplotlib.pyplot as plt
p=data[['y','y_pred']].plot(subplots=True,style=['b-o','r-*'])
plt.show()模型学习了100多次之后就停止了。
预测结果对比图如下:
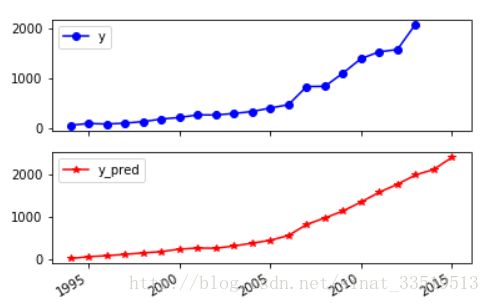
没有书中的效果好,是因为书中学习了10000次,结果肯定会更准确一些,但总体来说,效果也还可以。
总结
本章内容较为简单,新的实践内容其实就是灰色预测与Adaptive-Lasso变量选择,后者函数没有找到没办法,而前者,通过资料查找,灰色预测只适合短期内的预测,应用范围有限,如果长期则准确率会有所下降,感觉平时应用也挺少的,因为没怎么听说…