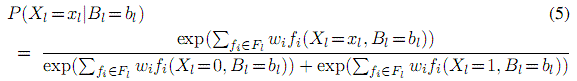马尔科夫逻辑网络
参考:条件独立与MRF
参考:置信传播
参考:Markov Logic Networks
参考:概率图模型
参考:MLN+举例
摘要:我们提出一个简单的方法将一阶逻辑和概率图解模型组合成一种表示形式。马尔科夫逻辑网就是一个每个准则或语句都有权重的一阶逻辑知识库,其中常数代表库中对象,还约定了一个基本马尔科夫网知识库中一个一阶逻辑准则的每个可能的基元都带有相应的权重。马尔科夫逻辑网推理是通过在回答问题所需的最小基元子集上运用马尔科夫链蒙特卡罗方法实现的。权重是从关系数据库通过拟似然度量的优化迭代高效学习获得,可选择地,额外的子句可运用归纳逻辑程序技术学得。使用一所大学内的一个真实世界数据库和知识库的实验表明这种方法大有前途。
关键词:统计关联学习,马尔科夫网,马尔科夫随机场,对数线性模型,图模型,一阶逻辑,可满足性, 归纳逻辑程序设计,基于知识的模式构建,马尔科夫链蒙特卡罗方法,拟似然,连接预测
介绍
马尔科夫逻辑网,是一个除了有穷集要求外没有其它限制的能将概率和一阶逻辑结合的非常简单的表示办法。我们为马尔科夫逻辑网的学习和推理开发了高效的算法,并在某个现实世界场景中进行了评估。
一个马尔科夫逻辑网就是一个每个准则都有权重的一阶逻辑知识库,可看成是构建马尔科夫逻辑网络的模板。从概率的视角看,马尔科夫逻辑网提供一种简洁的语言来定义大型马尔科夫网,能灵活地、模块化地与大量知识合并;从一阶逻辑的视角看,马尔科夫逻辑网能健全地处理不确定性、容许有瑕疵甚至矛盾的知识库,降低脆弱性。有许多统计关系学习领域的重要任务,如集合分类、链接预测、链接聚合、社会网络建模和对象识别,都自然而然地成为运用马尔科夫逻辑网推理和学习的实例。
马尔科夫网络
马尔科夫网(也叫马尔科夫随机场)是随机变量集x=x1,x2,…,xn的联合分布模型,它由一个无向图G和一个势函数Фk集合组成,每个随机变量是图上的节点,图的每个团在模型中都有一个势函数,势函数是一个非负实函数,它代表了相应的团的状态。马尔科夫网的联合分布如下
P ( X = x ) = 1 Z ∏ k ϕ k ( x k ) P(X=x)=\frac{1}{Z}\prod_{k} \phi_k(x_k ) P(X=x)=Z1∏kϕk(xk) (1)
其中x{k}是团中随机变量的状态,Z也叫配分函数,定义为Z 。将马尔科夫网络中每个团的势用状态的所有特征值加权后求和再取幂,就可方便地表示成对数线性模式
P ( X = x ) = 1 Z e x p ( Σ j ω j f j ( x ) ) P(X=x)=\frac{1}{Z}exp(\Sigma_j \omega_jf_j(x)) P(X=x)=Z1exp(Σjωjfj(x))
特征函数可以是表示状态的任何实函数,本论文将只讨论二元特征值。公式1是势最直接的表示,其中每个团每个可能的状态都有一个对应的特征值 fj(x),它的权重是wj,这种表示方法与团数量的幂相关。可是,我们可以自由地运用一些方法比如状态的逻辑函数等减少特征值数量,特别在团数量很大时能相比势函数方式提供一种更简洁的表示形式。马尔可夫逻辑网络就是利用了这一方式。
马尔可夫网的推理是NP完备问题。最被广泛使用的近似推理方法是马尔可夫链蒙特卡罗法(MCMC),特别是吉布斯采样法,它依次对每个随机变量在它们各自的马尔可夫毛毯中进行采样处理(一个节点的马尔可夫毛毯是一个节点能与剩余网络互相独立的最小节点集合,简单地说在一个马尔可夫网中,就是节点在图中的邻居)。边缘概率可通过对采样值的计数得到,而条件概率可将作为条件的随机变量值设定后运用吉布斯采样得到。另外一种流行的马尔可夫网推理方法是置信传播法。
求马尔可夫网权重的最大概似法或者最大后验概率法都不是封闭解,但是由于对数概似函数是权重的凹函数,可运用标准积分或优化的拟牛顿法高效求解 。另一种选择是迭代法。特征值可从数据中学得,比如通过贪婪地构建原子特征合取式。
一阶逻辑
一个一阶知识库是一个由一阶逻辑句子或规则组成的集合。组成规则的有四种类型的符号:常数、变量、函数和谓语,常数符号代表所涉及领域的对象,变量符号可在涉及领域的对象范围内变化,函数符号(例如,MotherOf)表示了对象组之间的映射关系,谓语符号代表了对象间的关系(如,Friends)或者对象的属性(如,Smokes),还需要说明哪些符号代表了域中的哪些对象、函数和关系。变量和常数可以有类型,那样的话常数只能代表同类型的对象,变量只能在同类型的对象范围中取值,例如,变量x可以代表人(如,Anna,Bob等),常数C可以表示一个城市(如,西雅图)。
一个词是代表域中对象的任意表达式,它可以是常数,变量或应用到一组词上的函数,比如,Anna、X、GreatestCommonDivisor(x,y)都是词。一个原子规则或原子是应用到一组词上的谓语(Friends(x,MotherOf(Anna)))。而规则是使用数量词和逻辑连接符从原子规则递归构建的。如果F1和F2是规则,那么下列的也是规则: ¬ F1(否定),当且仅当F1为假时取真值; F1 ∩ F2(合取),当且仅当F1和F2都为真时取真值; F1 ∪ F2 (析取),当且仅当F1或F2为真时取真值; F1 ⇒ F2 (蕴涵),当且仅当F1为假或F2为真时取真值;F1 ⇔ F2(等价) ,当且仅当F1和F2取值一样时取真值; ∀ x F1(全称量词),当且仅当F1对域中每个对象X为真时取真值; ∃ x F1(存在量词),当且仅当F1对域中至少一个对象X为真时取真值。
一个规则如果是可满足的,那么当且仅当至少在一个世界中是真的。一阶逻辑中基本的推理问题一般是确定一个知识库KB是否包含某个规则F,也就是在KB所有真的世界里F也真。这个常常用反证法证明:KB包含F当且仅当KB包含¬F无法满足。(于是,如果一个知识库含有矛盾,所有的规则也就矛盾了,因此,知识库需要非常尽心维护)。为了方便自动推理,规则常常被转换成一种正则形式,一种句子形式(也叫做合取范式(CNF))。一个范式的知识库是由一些合取的句子组成,而每个句子又由析取的文字组成。每个一阶逻辑的知识库都可通过机械的步骤转换成范式。在一阶逻辑中范式用于问题求解,这是一个健全的、无法反驳的推理方法。
基于一阶逻辑的推理仅是半可解的,因此,知识库往往使用一阶逻辑的有更多特性的限定子集来表示。Horn子句是一种最被广泛使用的子集,它的句子只允许最多一个肯定的文字。Prolog程序语言就是基于Horn子句逻辑,Prolog程序可以从库中搜索含有近似数据的Horn子句,这在归纳逻辑程序研究过。
表Ⅰ是一个简单的知识库和它的范式转换形式。请注意,这些规则在现实世界中通常是真的,但不总是真的。在大多数场景一些重要的规则往往很难表达为一直为真,这些规则仅捕捉到了相关知识的一部分。尽管善于表达,但是纯粹的一阶逻辑在人工智能实践中应用能力有限。许多特别的扩展办法被提出来解决这个问题,这个问题在更有限的命题逻辑范围内已被概率图模型很好地解决了。下一节将介绍将这些模型推广到一阶逻辑的办法。
表Ⅰ是一阶逻辑知识库和马尔可夫逻辑网的例子,Fr、Sm、Ca分别是Friends、Smokes和Cancer的缩写
| English | 一阶逻辑语言 | 范式 | 权重 |
|---|---|---|---|
| Friends of friends are friends. | ∀ x∀ y∀ zFr(x,y)∧Fr(y,z)⇒Fr(x,z) | ¬Fr(x,y)∨¬Fr(y,z)∨Fr(x,z) | 0.7 |
| Friendless people smoke. | ∀ x(¬(∃yFr(x,y))⇒Sm(x) | Sm(x)∨Fr(x,g(x)) | 2.3 |
| Smoking causes cancer. | ∀ xSm(x)⇒Ca(x) | ¬Sm(x)∨Ca(x) | 1.5 |
| If two people are friends,either both smoke or neither does. | ∀ x∀ yFr(x,y)⇒(Sm(x)⇔Sm(y)) | ¬Fr(x,y)∨Sm(x)∨¬Sm(y) | 1.1 1.1 |
马尔科夫逻辑网
一个一阶逻辑知识库可以看作是在一系列可能的世界上加上了一套硬约束:哪怕只与一条规则冲突也不行。马尔科夫逻辑网的基本想法就是要软化这些约束:一个可能世界如果与知识库规则冲突,不会不可能存在,而是可能性下降,冲突的规则数越少,可能性越大。每个规则都和一个反映其约束强度的权重关联:在其它情况一样的前提下,权重越高的,满足和不满足此规则的事件的对数概率差就越大。
定义4.1 马尔科夫逻辑网L是(Fi,wi)对的集合,其中 Fi代表一阶逻辑规则, wi是一个实数;有限的常数集为C = {c1,c2,…cn},马尔科夫网ML,C如下1、2来定义:
1、L中每个谓词的每个可能基元在ML,C中有一个二元节点,如果原子公式为真,节点的值就等于1,否则为0。
2、L中每个规则的每个基本可能在ML,C中有一个特征值,当这个规则为真时等于1,否则等于0,特征值的权重为 Fi 对应的wi。
马尔科夫网MLN中规则的语法是一阶逻辑的标准语法,自由(未限定)变量被认为是规则最外层的全称变量。
这个定义可以看作构建马尔科夫网络的模板。如果常数集不同,它会产生大小不同的网络,但是所有关于结构和参数的规则都是确定的(比如一个规则的所有可能都有相同的权重)。我们把它称作基本马尔科夫网,以示与一阶逻辑MLN的区别。从定义4.1、等式1和2可以得出,基本马尔科夫逻辑网概率分布如下
ni(x)是Fi在X中所有取真值的基本规则的数量,而x{i}是Fi中为真的原子,又有ϕi(xi)=ewi。请注意,虽然我们将马尔科夫逻辑网定义成对数线性模式,它们还可以定义成势函数积的样子,就如上面第二个等式。当硬约束和软约束并存时,这是最简便的方法(比如,当一些规则很确定时,不满足将导致事件不可能)。
按照定义4.1构建的ML,C的图结构是这样的:当且仅当两个节点相应的基本原子同时出现在L中的一个规则的至少一个基本形式时,这两个节点之间就有一条边。这样,ML,C的每个基本公式中的原子构成一个(未必最大的)集团。
图1展示了一个基本的马尔科夫网,它是由表1的最后两个规则和常数Anna和Bob定义的。图中的每个节点都是基本原子(比如,Friends(Anna,Bob))。当一对原子同时出现在某个基本规则时,它们之间就有一条弧。这个ML,C可以用来推测当知道Anna和Bob的吸烟习惯时他们朋友的可能性,或者当他们是朋友同时Anna有癌症时Bob得癌症的概率,等等。
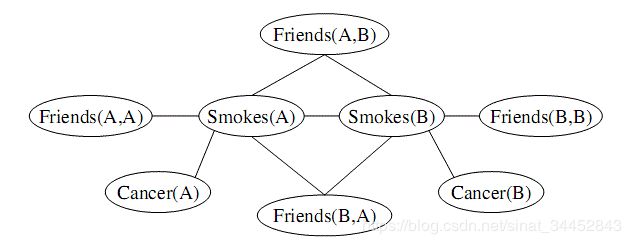
ML,C的每个状态代表了一个可能的世界,一个可能的世界就是一个对象集合、一个函数集合(映射对象组)和一组对象之间的关系;它们一起来确定每个基本原子都取真值。下面的几个假设保证了代表(L,C)的可能世界集是个有限集,又很好的独特定义了这些可能世界的概率分布,同时还与所涉领域和表达形式无关。这些假设在绝大多数实践应用中是合理的,大大简化了马尔科夫逻辑网的应用难度。有赖于此,我们可以轻松地讨论后面的几个例子。
假设1:命名唯一性。不同的常数代表不同的对象(Genesereth & Nilsson,1987)。
假设2:范围封闭性。只存在能用(L,C)中常数和函数符号表示的对象(Genesereth & Nilsson,1987)。
假设3:函数确定性。L中每个函数每个可能的值都确定在常数集C中。
最后这个假设可以让我们在基本化规则时将函数替换成它们的值,就只需考虑以常数作为参数的基本原子,这样就可以忽略(L,C)中所有的函数和常数构建无限原子集的情况,因为每个词都是C中确定的常数,包含它们的原子也就表示为包含对应的常数。 按定义4.1每个谓词的可能基形可以这样简单得到,将变量用C中常数替换,将函数也用相应的常数替换。表Ⅱ是在假设1、2、3基础上求基本原子规则的步骤。如果一个规则多于一条子句,那么它的权重在各个子句上平分;而一个句子的权重会被赋予它的每个基本形式。
表II 基本原子的构建
function Ground(F, C)
inputs: F, a formula in first-order logic
C, a set of constants
output: GF , a set of ground formulas
calls: CNF(F,C), which converts F to conjunctive normal form, replacing existentially quantified formulas by disjunctions of their groundings over C
F ← CNF(F, C)
GF = Φ
for each clause Fj ∈ F
Gj = {Fj}
for each variable x in Fj
for each clause Fk(x) ∈Gj
Gj ← (Gj \ Fk(x)) ∪ {Fk(c1), Fk(c2),..... Fk(cj)g} ,where Fk(ci) is Fk(x) with x replaced by ci ∈ C
GF ← GF ∪ Gj
for each ground clause Fj ∈GF
repeat
for each function f(a1,a2,.....) all of whose arguments are constants
Fj ← Fj with f(a1,a2,......) replaced by c, where c = f(a1,a2,......)
until Fj contains no functions
return GF
假设1(命名唯一性)可以去掉,如果引入等于谓词(Equals(x,y)或x=y)并将等于的自反、对称和传递性,以及对于任意二元谓词P,clip_image012,其余高阶的谓词和函数也一样,这些公理加入马尔科夫逻辑网的话。每对常数在最终形成的马尔科夫逻辑网中都有一个节点,1代表这对常数是同一对象,否则为0;这些节点之间以及和网络的其它部分的连接弧代表了上述的公理。这让我们有能力对两个常数的等同性进行概率推理,并成功地以此法为基础进行了对象识别(请参阅8.5节)。
如果知道未知对象的数量u,我们可以简单地引入u个任意新常数,这样假设2(范围封闭性)就可以去掉了。如果u不确定但是有限的,假设2也可以不用,办法是引入u的概率分布,用每个未知对象的数量对马尔科夫逻辑网基本化,规则F的概率可计算为clip_image014,MuL,C是有u个未知对象的基本马尔科夫逻辑网。而u如果无限的话,就需要将马尔科夫逻辑网扩展至无限常数集条件下。
让HL,C代表由L中的符号、(L,C海尔勃朗全域)中的常数构建的所有基词。如果将HL,C的每个对象看作常数,采取去掉假设1相同的步骤的话,假设3也可以去掉。例如,函数G(x)、常数A和B,这个马尔科夫逻辑网将有节点G(A)=A、G(B)=B等。这有可能引入无限多的新常数,需要相应扩展马尔科夫逻辑网。但无论如何,如果我们限定最大嵌套层数的话,得到的马尔科夫逻辑网还是有限的。
总之,只要范围是有限的,那么假设1-3都可以不要。我们相信马尔科夫逻辑网能扩展到无限领域,不过那主要是理论研究领域的事,我们以后再考虑。除非另外注明,本论文的接下来部分都基于假设1-3。
简单地将一个一阶逻辑知识库的每个规则赋予权重,这个库就变成一个马尔科夫逻辑网。例如,利用表Ⅰ最后两行的句子和权重构建的马尔科夫逻辑网, 当其它条件相同时,根据这个马尔科夫逻辑网可以得出,n个没有朋友的人不吸烟的概率要比所有没有朋友的人都抽烟的概率小e(2.3)n倍。值得注意的是,表Ⅰ的那些带全称量词的规则在现实世界都是错的,但是作为马尔科夫逻辑网的特征来看的话,却抓住了朋友友谊和吸烟习惯间的有用信息。比如,青少年朋友倾向于有相同的吸烟习惯。事实上,像表Ⅰ这样一个马尔科夫逻辑网简洁地表示了一个社会关系分析中的一个主要模型。
显而易见,马尔科夫逻辑网包含了命题逻辑概率模型的所有要素,下面详细说明。
命题 4.2:任意离散或有限精度的数字随机变量的概率分布都能用马尔可夫逻辑网表达。
证明:首先考虑布尔型的随机变量(X1,X2,…,Xn);我们为每个变量Xh定义一个不含参数的谓词Rh,再将表示(X1,X2,…,Xn)每个状态的规则加入到L中;这个规则是n个字的合取,当Xh为真时这个字取Rh(),否则取 ¬ Rh(),这个规则的权重为logP(X1,X2,…,Xn)(如果某些状态概率为0,我们就采用乘积形式,见等式3,用ϕi()表示i状态的概率);因为L中所以谓词都没有参数,L所定义的马尔科夫逻辑网每个变量Xi 就是一个节点,而且这个ML,C与常数C无关;对于任一状态,相应规则为真,其它规则为假,这样等式3就代表了初始分布(注意Z=1)。只要为每个变量定义一个没有参数的谓词,将上述方法推广到任意离散变量就很简单直接;有限精度数字随机变量也一样,只要用布尔矢量表示这些变量就可以了。(证毕)
当然,只要为相应的要因定义规则(马尔科夫网的任意特征、节点状态以及贝叶斯网络中的父节点),象马尔科夫网、贝叶斯网这样的紧凑要因模型仍然能用马尔科夫逻辑网简洁地表示。
一阶逻辑(在假设1-3下)是马尔科夫逻辑网的一个特例,下面将接着讨论,这个特例的所有权重都相等且趋向无限大。
命题4.3 设KB是一个可满足的知识库,L是一个所有规则都带有权重的代表KB的马尔科夫逻辑网,C代表KB中出现的常数集,Pw(x)是由ML,C得出的事件集x的概率,XKB是满足KB的事件集,F为一阶逻辑的任意规则,那么有:
1、∀ x∈XKB limw→∞ Pw(x) = |XKB|-1
∀ x∉XKB limw→∞ Pw(x) = 0
2、∀ F KB蕴含F当且仅当 limw→∞ Pw(F) = 1
证明:设k为ML,C中基本规则的数量,利用等式3,若x∈XKB则Pw(x)=ekw/Z,若 x∉XKB则Pw(x)≤e(k-1)w/Z;所有x∈XKB等概率,又limw→∞ P(x\XKB)/P(XKB)≤ limw→∞ P(|x\XKB|)/P(|XKB|)e-w=0(第一点证毕)。由蕴含的定义,所有满足KB的事件也满足F,设XF为满足F的事件集,那么有 XKB⊆XF,而Pw(F) = Pw(XF) ≥ Pw(XKB),由第一点limw→∞ Pw(XKB) = 1,所以,limw→∞ Pw(XF) = 1;反过来,如果 limw→∞ Pw(XF) = 1,那么每个非零概率的事件极限上必须满足F,这就包含了 XKB中 所有的事件。(证毕)
换句话说,在所有相等的无穷大权重的极限中,马尔科夫逻辑网表示了满足知识库的所有事件的一个均匀分布,所有蕴含问题可以通过计算问题规则的概率是否为1来判断。即使在权重是有限值的情况下,从下面的观念来看,一阶逻辑已被植入到了马尔科夫逻辑网中。不是一般性,我们假设权重都是非负的(若一个规则的权重w为负值,我们就用它的否定形式来替换,这时权重为-w),如果一个由马尔科夫逻辑网L中规则构成的知识库是可满足的,那么,对于任意常数集C来说,满足情况的模式分配就是马尔科夫逻辑网所代表的概率分布,这是因为这些模式都是有最大值∑iwini(x)(见等式3)的事件,这个表达式在所有规则的所有可能为真时取最大值(比如,满足知识库)。但不管怎样,马尔科夫逻辑网和通常的一阶逻辑知识库不一样,当包含矛盾的规则时,它也能产生有用的结果。一个马尔科夫逻辑网也可以通过一些知识库的合并来获得,即使这些知识库有部分不相容。这个特性在某些领域非常有潜力,如语义网(Berners-Lee et al.,2001)和大规模协作(Richardson & Domingos,2003)。
有一个马尔科夫逻辑网一般化一阶逻辑的简单而有趣的例子,设一个马尔科夫逻辑网只有一条规则:∀x R(x)⇒ S(x)、权重为w,常数集C = {A};这里只有4个事件:{¬R(A),¬S(A)}、{¬R(A),S(A)}、{R(A),¬S(A)}、{¬R(A),S(A)},从等式3可以得出:P({R(A),¬S(A)})=1/(3ew+1)、其它三个事件的概率是ew/(3ew+1)(除数是配分函数Z,见第二章);这样,如果w>0,这个马尔可夫网使得与∀x R(x)⇒ S(x)不一致的事件比其它的三个可能性更低一些;从上我们得到P(S(A)|R(A)) = 1/(1+e-1),limw→∞P(S(A)|R(A)) = 1,又回到了一阶逻辑的结果。
实践中,我们发现将每个谓词单独加到马尔可夫逻辑网中非常有用。换句话说,对于谓词R(x1,x2,…),我们加入规则∀x1,x2… R(x1,x2,…),权重为wR,这使得单句的权重能与谓词边际分布较好地匹配,让那些非单句的权重仅依赖与相关的谓词。
如果对权重有一些直觉上的理解,那么对我们手工构建或阅读学习一个马尔可夫逻辑网就有帮助。简单地说,一条规则F的权重就在其它条件不变时为真或为假的对数差异。然而,F往往和其它规则有着共同的变量,想要反转F同时保持其它规则不变往往不太可能,规则F的概率和它的权重之间也就不再存在一对一关系。不过,如果我们从最大熵分布的约束或者从学习经验概率的最大似然权重来看,总的来说所有规则的概率决定了所有的权重(Della Pietra et al.,1997)。因此设定马尔可夫逻辑网的权重最好的办法是:写下每个规则应有的概率,把它们当做经验频率,然后运用第六章的算法来学习这些权重;相反地,从一个马尔可夫逻辑网学习到的权重从统计上可以看作暗含着规则的经验概率。
如果使用类型化的常数和变量,由于只需要将变量基本化为相同类型的常数,那么,基本马尔可夫逻辑网的大小可以大大减小。不过,即使这样网络还会非常巨大。幸运的是,正如下一章节介绍的,有许多推理问题并不需要基本化整个马尔科夫逻辑网来解决。
推理
马尔科夫逻辑网可以回答类似“规则F2成立的前提下,规则F1成立的概率是多少?”的任意问题。如果F1和F2是一阶逻辑的两个规则,C是出现在F1、F2中的常数的有限集合,而L代表马尔科夫逻辑网,那么
其中XFi是Fi成立的事件集,P(X=x|ML,C)由等式3得出。一般图形模型中的条件查询都是等式4的特例,其中F1、F2和L中的谓词都没有参数,而且规则都是合取式。在一阶逻辑中一个知识库是否蕴含规则F实际上就是P(F|LKB,CKB,F)是否等于1的问题,LKB是将知识库中所有规则权重都设成无穷大后等到的马尔科夫逻辑网,CKB,F是KB或F出现的常数集合。在F2成立的条件下,利用等式4计算出P(F|LKB,CKB,F)就能回答这个问题。
即使在规模很小的领域直接利用等式4来计算都是棘手的,因为马尔科夫逻辑网推理包含了#P-complete复杂度的概率推理,而逻辑推理在有限域也是NP-complete复杂度的,所以不能寄予期望。可是,提高推理运算效能的许多大数技术都可以运用到马尔科夫逻辑网上,这是因为马尔科夫逻辑网能使用细粒度的知识库,包含了上下类的独立性,推理就要比普通的图模型更有效;在逻辑方面,具备了概率语义的马尔科夫逻辑网能够进行高效的近似推理。
原则上,P(F1|F2,L,C)可以使用马尔科夫蒙特卡洛算法近似得出,只要拒绝转移到F2不成立的状态,计数F1成立的取样即可。但即使这样对于任意规则,这种算法还是太慢了。当F1和F2都由基词的合取式组成时,我们准备了一个的算法来替代,虽然没有等式4的普遍性,但现实中的问题往往是这种形式,而且我们回答问题时将比直接应用等式4更有效率。研究提高的算法(比如要回答的问题含有变量)是将来的一个重要研究方向。和知识库模式构建类似,这个算法分为两个阶段。第一阶段求得计算P(F1|F2,L,C)所需基本马尔科夫逻辑网的最小子集M,如表Ⅲ所示。任何事实上为真的基本规则可以忽略,相应的弧也可以省略掉,这样等到的网络规模就大大缩小了,算法也就很快了。在最坏的情况下,得到的网络有O(|C|a)个节点,其中a是所有谓词的最大参数数量,实践中a往往很小。
表Ⅲ 马尔科夫逻辑网推理中的网络构建
function ConstructNetwork(F1, F2, L, C)
inputs: F1, a set of ground atoms with unknown truth values (the “query”)
F2, a set of ground atoms with known truth values (the “evidence”)
L, a Markov logic network
C, a set of constants
output: M, a ground Markov network
calls: MB(q), the Markov blanket of q in ML,C
G ← F1
while F1 ≠ ∅
for all q ∈ F1
if not q ∈ F2
F1 ← F1 ∪ (MB(q)\G)
G ← G ∪ MB(q)
F1 ← F1 \ {q}
Return M, the ground Markov network composed of all nodes in G, all arcs between them in ML;C, and the features and weights on the corresponding cliques
第二阶段将F2相关节点设为F2成立的值,然后进行推理。我们应用的是吉布斯采样法,但是其它推理方法也可以使用。基本吉布斯方法是在一个基本原子的马尔科夫毛毯范围内对它进行取样。一个基本原子的马尔科夫毛毯是和它一起出现在某些基本规则中的基本原子集合。一个基本原子Xl在它的马尔科夫毛毯Bl状态为bl时的概率为
其中Fl是Xl出现的基本规则集合,fi(Xl=xl,Bl=bl)是当Xl=xl,Bl=bl时第i个基本规则的特征值(0或者1)。对于那些在某些事件中确定为真的原子,就可以使用块操作(比如在一步中将一个原子设为真,其它为假,在它们的联合马尔科夫毛毯中取样)。这样一个基词合取式的估计概率就是当马尔科夫链收敛时这些基词为真的取样所占的比例。因为概率分布往往有多种样式,我们需要多次运行马尔科夫链。当一个马尔科夫逻辑网是范式时,我们可以缩短预处理时间,运用MaxWalkSat这样一个用于求解加权可满足性问题的局部搜索算法(比如,找到一个真的赋值使得满足的规则的权重之和最大)(Kautz et al.,1997)来搜寻模式再运行马尔科夫链。当存在硬约束时(规则的权重无穷大),MaxWalkSat能发现满足它们的区域,然后我们可再用吉布斯采样法对这些区域采样来估算概率。
学习
我们可以从多个关系数据库中学习马尔科夫逻辑网的权重(为了简便下面只讨论一个数据库的情况,一般化到多个数据库太琐碎就省略了)。先引入闭型世界假定(Genesereth & Nilsson,1987):如果一个基本原子不在数据库中,那我们就假定它为假。如果有n个基本原子,那么数据库最有效是矢量形式x=(x1,…,xl,…,xn),xl是第l个基本原子的值(如果在数据库中为1,否则等于0)。有了数据库,原则上马尔科夫逻辑网的权重可以使用标准的方法学习到,如下:如果第i个规则在数据x中有ni(x)个真的基本形,那么等式3的对数概似函数对权重wi的导数为
其中的求和是对所有事件库x‘,而Pw(X=x’)是P(X=x’)用当前的权重矢量w = (w1,…,wi,…)计算的。换句话说,第i部分的斜率就是它为真的基本形式与数学期望的差。不幸的是,即使一个简单规则要数它的基本形式数量也是很棘手的事,如下(Dan Suciu)。
命题6.1 对一个一阶逻辑规则的真基本形计数是一个和它长度相关的#P-complete难题。
证明:计数满足单调二元合取范式命题的赋值数是个#P-complete难题(Roth,1996)。这个问题可简化为如下的计数一个知识库的一条一阶逻辑规则的真基本形问题,设一个知识库由R(0,1)、R(1,0)、R(1,1)基本原子组成,有一个单调二元合取范式规则Ф由谓词R(xi,xj)的合取式组成,而谓词如xi∨xj(比如(x1∨x2)∧(x3∨x4)为R(x1,x2)∧R(x3,x4))。这样满足二元范式的赋值与Ф为真的基本形之间有一一对应关系。(证毕)
在大领域一条规则的真基本形数量可以估算,通过均匀取样并检查是否为真来实现。在小的领域,如下面我们的实验一样,我们使用一种有效的递归算法来得到精确的数量。
等式6的另一个问题是计算为真的基本形的数学期望值同样棘手,需要对整个模型进行推算。另外,高效的优化方法还需要计算对数似然(等式3)和配分函数Z,这可以使用蒙特卡洛最大似然估计法(MC-MLE)(Geyer & Thompson,1992)。可以,在我们的实验中是使用吉布斯采样法来计算蒙特卡洛最大似然值,微分在合理时间内往往还没有收敛,而使用没有收敛的链来采样往往得不到好的结果。
在空间统计、社会网络建模、语言处理等领域广泛使用的一种更有效的选择是优化拟似然方法
MBx(Xl)是Xl的马尔科夫毛毯的状态。拟对数似然的微分是
其中ni(x[xl=0])是当我们强制xl=0同时其余不变的情况下第i条规则为真的基本形数量,ni(x[xl=1])也同样。计算这个表达式(或者等式7)不需要对整个模型进行推测。我们还用有限记忆空间的BFGS算法对对数拟似然法进行优化(Liu & Nocedal,1989),使得计算在下面几个方面更高效:
忽略第i条规则中不出现的谓词,等式8的求和速度大大加快;
ni(x)、ni(x[xl=0])、ni(x[xl=1])不随权重变化,只需要计算一次;
因为ni(x)=ni(x[xl=0])=ni(x[xl=1]),只改变一个基词的值不会改变基本规则的真假,因此可以忽略。特别的对任何有至少两个为真的基词的句子也成立,这往往是绝大多数基本规则的特性。
为了避免过度拟合,我们先针对每个权重利用高斯法对拟似然方法进行了变形。
可以使用归纳逻辑编程技术来精炼已有或者学习新增的规则,甚至从头学习一个马尔科夫逻辑网。为此,我们使用了CLAUDIEN系统(De Raedt & Dehaspe,1997)。和其它只学习霍恩子句的归纳逻辑系统不同,CLAUDIEN能学习任意的一阶逻辑句子,因此非常适用于马尔科夫逻辑网,还可通过设定特别语言偏好使用CLAUDIEN来精炼马尔科夫逻辑网的结构。下一步我们计划象MACCENT解决分类问题(Dehaspe,1997)一样,将象Della Pietra et al发明的技术或方法等一般化到一阶逻辑领域,将结构学习功能完全引入到马尔科夫逻辑网中。
实验
我们用描述华盛顿大学计算机科学工程系的知识库来测试马尔科夫逻辑网。该领域由12个谓词、10大类2707个常数组成,类型有:出版物(342个常数)、人物(442)、课程(172)、项目(153)、学期(20)等等;谓词有:Professor(person)、Student(person)、Area(x, area)(x可以取出版物、人物、课程和项目的值)、AuthorOf(publication,person)、 AdvisedBy(person,person)、YearsInProgram(person,years)、CourseLevel(course, level)、TaughtBy(course,person,quarter)、 TeachingAssistant(course,person,quarter)等等;另外还有10个等于谓词:SamePerson(person,person)、 SameCourse(course, course)等等,如果两个参数值代表相同的常数,那么就为真。
使用变量类型后,所有可能的基本原子(第六章的n)总数为4106841,而数据库含有3380个元组(比如3380个为真的基本原子)。我们通过抓取系网站的网页(www.cs.washington.edu)获取数据,出版物和作者之间的关系通过BibServ数据库(www.bibserv.org)所有记录中的作者字段至少含两部分(名、姓)获得。
四个自愿者每个人都提供了一套一阶逻辑规则来描述这个领域,为我们建立了知识库(这些自愿者不知道数据库中的元组,但他们都是系里的成员,对整个系有一定的了解)。整合起来后我们获得了一个有96条规则的知识库。整个知识库、数据、算法的参数、自愿者的指示在http://www.cs.washington.edu/ai/mln可以找到。知识库中有类似这样的规则:学生不是教授;每个学生至少有一个导师;如果一个学生是一篇论文的作者,那么他的导师也是;研究生只上他导师的课程;一篇出版物的作者至少有一位是教授;物理博士第一阶段的学生没有导师等等。请注意上述规则并不总是正确的,但通常是。
为方便训练和测试,我们按人工智能、图像、编程语言、系统和理论5个领域将数据库分成5个子数据库。教授和课程这些常数被手工分配到各个领域,其它常数被赋予它们最常出现的领域,然后元组被添加到其中常数所属的领域,含有不同领域常数的元组被删除以避免训练测试混乱。这些子数据库平均在58457个可能的基本原子中有521个真的基本原子。
我们使用了一个留下一个的测试策略,每次测试一个领域时采用其余四个领域的训练结果。两个测试任务是预测谓词AdvisedBy(x,y):任务A,其它信息都知道;任务B,除了Student(x) 和Professor(x)以外,其它信息都知道。在两个例子中我们都测量了所有领域中谓词AdvisedBy(x,y)的基本形的平均条件对数似然率,画出查准率查全率曲线,然后计算曲线下的面积。这项任务就是连接预测的一个实例,这个问题在统计关系学习(见第8章)中广泛关注。测试中所有知识库被转化成范式,时间结果是基于2.8G赫兹奔4处理器的主机。
-
测试的系统
为了评估使用逻辑和概率推理的马尔科夫逻辑网,我们计划将它与纯逻辑法和纯概率方法相比较,同时我们还对使用归纳逻辑程序技术的规则自动归纳感兴趣。下面各小节详细描述了用于比较的各类系统。
1.1 逻辑
使用纯逻辑实验的主要目的是为了帮助我们回答一个重要问题,那就是将概率引入逻辑知识库是否能够提升我们对某领域建模的能力。为了做到这一点需要我们在回答问题时仅使用逻辑推理,但实际上这非常复杂,因为计算对数似然率和查准率查全率曲线下的面积需要概率,或者至少对测试中为真的每个基本原子要有“确信度”的衡量值。为此,我们使用了以下方法来近似,设KB为一知识库,E为已证实的原子集合,XKB∪E为满足KB∪E的事件集,那么,我们查询的原子q的概率为P(q)=|XKB∪E∪q|/|XKB∪E|,这是q在XKB∪E为真的比例。
一个更严重的问题是知识库可能不一致(从自愿者收集的知识库更是如此),这时P(q)公式的分母为0(设想一下一个不一致的知识库可能包含任意规则)。为了解决这个问题,我们重新将XKB∪E定义为满足最大可能基本规则数量的事件集合,再用吉布斯采样法对这个集合进行采样,每次链的初始状态由WalkSat方法来获得。每一步吉布斯采样都有概率:如果新状态满足的规则大于当前状态,那么,概率为1(也就是当前状态的概率应该为0);如果满足的规则数量与当前状态相等,则概率等于0.5;如果新状态满足的规则数量要少则概率为0。然后我们再用最大满足的规则来计算概率。实际上,等同于从知识库中构建一个权重无穷大的马尔科夫逻辑网。
1.2 概率
另外一个需要实验来帮我们回答的问题是是否已经存在足够强大的(命题)概率模型而不再需要马尔科夫逻辑网的表达能力。 为了应用这种模型,这个领域需要定义一些有表现力的属性值来命题化,在这种高度关联的领域中创建好的属性对于命题学习者来说非常困难。无论如何,在平衡了更多潜在关系信息表达能力和极其冗长的属性矢量后,我们定义了两套命题属性:order-1和order-2。前者包含了查询谓词中个体常数的特性,后者包含了常数之间关系的特性。
对于order-1的属性,我们为每对(a,b)定义一个变量,a是询问谓词的一个自变量;b是某个谓词的自变量,它的值和a一样。我们定义的变量代表这个谓词为真的基本形的比例。例如AdvisedBy(Matt,Pedro)有:Pedro是否是学生,Pedro的出版物占比,Matt当助教的课程占比等等。
order-2属性是这样定义的:给定询问谓词Q(q1,q2,…,qk),考虑所有k个谓词和k个常数q1,q2,…,qk一一对应集合集,例如Q是AdvisedBy(Matt,Pedro)那么{TeachingAssistant(-,Matt,-),TaughtBy(-,Pedro,-)}是其中一个集合,这个例子就有2K个属性,每个对应于k个谓词的某个为真的基本形。属性的值等于训练中当未赋值的变量被赋予相同的值时,谓词集有特定真赋值的次数。例如,上述变量为“CSE546”和“Autumn0304”,集合{TeachingAssistant(CSE546,Matt,Autumn0304),TaughtBy(CSE546,Pedro,Autumn0304)}在训练时有一些为真的赋值(比如,{True,True},{True,False}……),属性值就是满足{True,True}为真赋值的常数集数量;{True,False}也一样;以此类推。查询谓词AdvisedBy(Matt,Pedro)的order-2属性举例有:Pedro教的课程中Matt任助教的频度(反过来不任助教的频度),有多少出版物是Matt和Pedro一起写的,等等。
最后得到的28个order-1属性和120个order-2属性(任务A)通过训练学习被我们分散到5个等频度的桶中,我们使用了两种命题学习方法:简单贝叶斯(Domingo & Pazzani,1997)和贝叶斯网络(Heckerman等,1995)(每个节点最大4个父节点,结构和参数使用VFBN2算法(Hulten & Domingos,2002)求得)。order-2属性能帮助简单贝叶斯分类,但是降低了贝叶斯网络分类的性能,因此我们报告简单贝叶斯结果时使用order-1和order-2属性,而贝叶斯网络仅仅用order-1属性。
1.3 归纳逻辑程序
我们起始的知识库是自愿者提供的,但是我们对能否用归纳逻辑程序方法自动得到也感兴趣。前面提到过,我们使用CLAUDIEN方法从数据中归纳知识,CLAUDIEN是这样运行的:本地范围、最小精度0.1、使用最小覆盖、最大复杂度10、广度优先搜索。CLAUDIEN的搜索空间由它的语言偏好决定,我们架构这样的语言偏好以允许:一个句子最多3个变量;一个句子中谓词数量不限;一个句子中一个谓词至多以二次肯定形式出现和二次否定;谓词的自变量有类型。为了最小化搜索,改善结果,我们不使用等于谓词(如SamePerson)。
除了从训练数据中归纳规则,我们还对自动优化由自愿者提供的知识库感兴趣。CLAUDIEN本身没有这个功能,但可以构建一个语言偏好来模拟,对于知识库的每个规则我们允许CLAUDIEN这样做:(1)移除任意数量的词;(2)增加至多v个新变量;(3)增加至多l个新词。我们在一台Sun-Blade 1000主机上对集合{(1,2),(2,3),(3,4)}的每对(v,l)运行CLAUDIEN24小时,三个结果都很相近,我们报告了(3,4)的结果。
1.4 马尔科夫逻辑网
我们要将上述系统与马尔科夫逻辑网比较。这些马尔科夫逻辑网使用均值为0、方差为1的高斯分布的权重来训练,初始权重都设为0。为了优化,我们使用的L-BFGS的Fortran版本(Zhu等 1997和Byrd等 1995),所有参数都是缺省值,收敛精度为10-5。用第5章描述的吉布斯采样法来进行推理,10个马尔科夫链并行,马尔科夫链的初始状态由MaxWalkSat确定。吉布斯采样步数由DeGroot和Schervish的准则(2002,pp.707和740-741)来决定,采样一直要进行到我们有95%的确信度,也就是说在95%的节点中真值的偏差在1%之内(忽略一直为真或假的节点),采样的最小步数和最大步数分别为1000和500000,每步一次采样。通常,推理会在5000-10000步间收敛。结果对设置的收敛精度不敏感。
- 结果
2.1 用MC-MLE来训练
最初我们使用蒙特卡洛最大似然法来训练马尔科夫逻辑网,用了10个吉布斯链,初始状态与相应一阶逻辑谓词为真的概率对应。因为每步仅少许满足的句子需要改变,吉布斯采样每一步运行得很快,在华盛顿大学计算机科学工程系这个例子上,我们的应用每步约4-5毫秒。我们用最大穿越所有谓词的Gelman R准则(Gilks等,1996)来判断这些链是否达到它们的平稳分布。因为直觉告诉我们,大多数原子总是假的,对它们重复采样没什么效率,所以,为了加速收敛,我们在吉布斯采样中优先采样在数据中或初始状态中为真的原子,这样在均匀选择原子基础上可以提高收敛速度大约一个数量级。尽管进行了这些优化,吉布斯采样法还是花过分长的时间来达到一个合理的收敛门限(比如,R=1.01)。在运行了24小时后(大约每链2百万步吉布斯采样),所有训练集的R值平均为3.04,没有一个训练集R值低于2(除了在开始阶段短暂地接近1.5外)。我们估计将花费20至400天来完成R值为2.0这样一个弱收敛门限的训练,因此必须考虑使用象L-BFGS这样迭代以寻找最小值。如果我们忽视收敛门限和缩短训练时间到小于10个小时,实验证明得到的模型会很差。只有有了象Swendsen-Wang算法(Edwards & Sokal,1988)这样的MCMC改进技术,加上能更好地选择初始状态和近似计数,MC-MLE才会实用,用它的目前版本来训练不太可行。(注意:在学习过程中MCMC是对整个基网运算的,太大了无法应用MaxWalkSat)
2.2 用拟似然来训练
和MC-MLE相反,拟似然法训练相当快。正如第6章讨论,一旦初始句子和满足的基本原子计数完成,训练的每次迭代可以做得相当快。平均计数时间花费2.5分钟(5组测试),而每次训练平均255次L-BFGS迭代,一共16分钟。
2.3 推理
推理也相当快。在知道全部信息(x,y)条件下,推算所有AdvisedBy(x,y)概率,人工智能专业的测试数据(4624个原子)花了3.3分钟;图形专业的(3721个原子)花了24.4分钟;程序设计专业(784)花了1.8分钟;系统专业(5476)用了10.4分钟;理论专业(2704)用了1.6分钟。吉布斯采样步数范围在4270-500000之间,平均124000,而每次吉布斯采样大约18毫秒,每秒200000-500000步。在知道部分信息条件下,推理的平均时间是14.8分钟(全部信息是8.3)。
2.4 比较
我们对比了12个系统:知识库(KB)、CLAUDIEN(CL)、以知识库为语言偏好的CLAUDIEN(CLB)、KB+CL、KB+CLB、MLN(KB)、MLN(CL)、MLN(CLB)、MLN(KB+CL)、MLN(KB+CLB)、简单贝叶斯(NB)和贝叶斯网络学习(BN)。在所有这些系统中我们都对概率使用了加一平滑。
表Ⅳ汇总了这些结果。图二显示了所有领域的查准率/查全率曲线(也就是所有AdvisedBy(x,y)原子的平均),图三至图七分别显示了5个领域的查准率/查全率曲线。马尔科夫逻辑网显然比其它系统更精确,展示了这种方法的前途。纯逻辑和纯概率方法常常遭受需推断中间谓词的困扰而马尔科夫逻辑网大都不受影响;简单贝叶斯在一些测试集计算AUC很好,但在其它集合很差,它计算CLL都一样差;CLAUDIEN自己都做得不好,加入到马尔科夫逻辑网的知识库时也没什么提高,使用CLAUDIEN来提炼知识库在AUC时表现不好,但在算CLL时比用CLAUDIEN白手起家要好;总之,效果最好的逻辑方法是KB+MLN,但实验结果要比最好的马尔科夫逻辑网逊色很多。一般来说,在50%查全率左右时查准率急降是因为数据的不完整,因而只能确认一小部分的AdvisedBy关系。检查显示在非常低查全率下偶然几次小的查准率急降是因为学生在共著许多出版物后毕业或者更换了导师。
统计关系学习的任务
许多统计关系学习的任务可以精确地用马尔科夫逻辑网表达,使得本文所介绍的算法可以直接得以利用。在本章中,我们将用5个关键任务来例证:集合分类、链接预测、基于链接的聚合、社会网络建模和对象识别。
-
集合分类
普通分类任务的目标是根据对象的属性来预测它的类别,集合分类还需考虑相关联对象的类别(Chakrabarti等(1998),Taskar等(2002),Neville和Jensen(2003))。属性可以用马尔科夫逻辑网的谓词形式A(x,v)表示,其中A代表一个属性,x表示对象,v是x的A值。每一个类别有一个指派的属性C,用C(x,v)表示,v是x的类。这样分类任务就简单地变为在已知A(x,v)前提下对所有x和v推导C(x,v)是否为真的问题。普通分类可看成在已知A(x,v)前提下对所有xi和xj而言它们的C(xi,v)和C(xj,v)互相独立的特例。在集合分类中,C(xi,v)的马尔科夫毛毯含有其它C(xj,v),甚至在已知A(x,v)后也是如此。对象之间的关系可以用谓词R(xi,xj)表示,显而易见这还需要再一般化,比方C(xi,v)和C(xj,v)通过间接的还不知道的谓词互相依赖的,甚至可能还包含了谓词R(xi,xj)。
-
链接预测
链接预测任务的目标就是要在知道对象的属性和其它可能的关系(Popescul和Ungar(2003))下来判断两个感兴趣的对象之间是否存在一种关系(比如,安娜是否是鲍勃的物理学博导?)。这个问题的马尔科夫逻辑网表示形式和集合分类一样,唯一不同的是推理的目标从C(x,v)变成了感兴趣对象间的R(xi,xj)。我们的实验就是链接预测任务。
-
基于链接的聚合
聚合的目标是将相同属性的对象组合起来。在基于模型的聚合中,我们设产生式P(X)=∑CP©P(X|C),其中X是对象,C为簇,那么P(C|X)就是X在簇C中的程度。在基于链接的聚合中,对象以它们之间的链接来聚合(对象关联越紧密越可能属于同一个簇)或它们的属性来聚合。在马尔科夫逻辑网中,可设一个未观测谓词C(x,v)代表x属于簇v,然后将它和其它观测到的谓词加入网中(如R(xi,xj)表示链接、A(x,v)表示属性)。这样基于链接的聚合就可通过马尔科夫逻辑网学习来解决,簇成员的程度由原子C(x,v)的条件概率得出。
-
社会网络建模
社会网络就是图,图的节点代表社会角色(如人),弧代表它们之间的关系(如友谊)。社会网络分析(Wasserman和Faust,1994)关注于为相关角色的属性和链接建模。例如,两个角色之间形成链接的概率依赖于类似的它们属性;反过来,两个链接的角色更可能有某些特定的属性。这些模型都是典型的马尔科夫逻辑网,能精确地用公式∀ x∀ y∀ v R(x,y) ⇒ (A(x,v)⇔A(y,v)),其中x和y是角色,而这个规则的权重代表了关联性和属性类似性之间相关的强度,例如,朋友之间倾向于有相同的吸烟习惯的模型可用规则∀ x∀ y Friend(x,y) ⇒ (Smoke(x) ⇔ Smoke(y))(表1)。马尔科夫逻辑网不仅能描述先有的简单的社会网络模型,而且还能描述更复杂的模型(比如用多类型关系和属性的规则,更复杂的依赖关系等)。
-
对象识别
对象识别(记录关联、重复删除等等)需要解决判断数据库中记录是否与现实世界某一实体相同(例如目录数据库中哪些代表了同一个出版物)的问题。对许多公司、政府机构、大规模的科研项目来说,这个问题非常关键。在马尔科夫逻辑网中,可以采用第4章那样除去命名唯一性假设,定义一个等于谓词Equals(x,y)(或就x = y)意思是“x与y代表一样的现实世界实体”。这个谓词同时应用到记录和字段上(例如,“ICML” = “Intl. Conf. on Mach. Learn.”)。记录匹配和字段匹配的依赖关系可用规则∀ x∀ y x = y ⇒ (fi(x)⇔ fi(y))表示,其中x和y是记录,fi(x)是返回x第i个字段的函数。我们已经成功地将这方法应用到Cora数据库中以剔除重复的计算机论文(Parag和Domingos,2004)。由于它能够将信息匹配向被匹配记录中各个字段传播,因此能有效地处理集合对象识别问题,在试验中胜出一个一个独立匹配的传统方法许多。比方说,匹配两个对象后可让我们确定“ICML“和”MLC“代表同一对象,接下来又能帮助匹配另外含有”ICML“和”MLC“的对象。马尔科夫逻辑网还能在重复删除系统方便地、标准化地、一致地引入附加信息,比如传递闭包可通过加入规则∀ x∀ y∀ z (x = y)∧(y = z) ⇒ x = z来引入,权重可从数据中学习得到。
相关工作
逻辑和概率方面有大量的文献,这里我们仅关注和统计关系学习有关的,再谈论它们与马尔科夫逻辑网的关系。
-
早期工作
试图在人工智能中将逻辑和概率结合起来最早至少可以追溯到Nilsson(1986)、Bacchus(1990)、Halpern(1990)和其他合作者(Bacchus等,1996),他们从理论角度对此问题进行了详细研究。他们区分了统计语句(如,我们系65%的学生是本科生)和概率事件语句(如,安娜是本科生的概率为65%),然后提出了从前者算出后者的方法。他们认为一个知识库无法确定随机事件完全、唯一的分布,需要其它的设想来获得。Bacchus等设想了许多方法,它们都有相当的局限性(比如,所有和知识库并存的世界都一样)。相反,将知识库看成马尔科夫网的模板,马尔科夫逻辑网可以表示任意事件集的任意分布。
Paskin(2002)延续扩展了Bacchus的工作,他将概率与一阶逻辑规则一一对应起来,使得最大熵的分布与它们的概率一致。这种表示方法仍然非常脆弱,只要一个事件与一个全称的基本规则相矛盾后就会象和所有规则相矛盾一样变得不可能出现。相反,在马尔科夫逻辑网中,象∀x Smoke(x) ⇒ Cancer(x)这样的规则对事件的影响会逐渐随着不得癌症吸烟者数量的增加而减弱。
-
基于知识的模型构建
基于知识的模型构建(KBMC)是逻辑程序和贝叶斯网络的组合(Wellman等 1992、Ngo和Haddawy 1997、Kersting和De Raedt 2001)。和马尔科夫逻辑网一样,KBMC的节点代表基本原子。在霍恩知识库下,KBMC能回答查询问题,它先通过搜索找到证明所需的所有后向链和代表事实的原子,用这些原子构建一个贝叶斯网络,然后再在这个网络上进行推理。网络中一个原子的双亲是代表以此节点为头的语句主体的确定AND节点,而后一个节点的条件概率就可用一个组合函数来计算(比如,noisy OR、逻辑回归或任意的条件概率表)。马尔科夫逻辑网与KBMC相比有很多优势:它们能使用任意规则(不仅仅霍恩子句);能在任意方向上推理;它们避开了困扰贝叶斯网络的循环问题;不需要为语句引入专门的组合函数。
将域中每个一阶逻辑谓词Pk(…)写成规则的话,一个KBMC模型可以翻译成马尔科夫逻辑网形式。每个规则是Pk(…)和它父节点文字的合取式。这些文字的一个子集是否定的;肯定和否定的每种组合都有一条规则;规则的权重w = log(p/(1-p)),其中p是父节点为真时根据组合函数得出的子谓词概率。如果组合函数是逻辑回归,它可仅用规则数量的线性表示,这得益于事实上逻辑回归是一个每个预测和响应之间是二元团的马尔科夫网。Noisy OR也同样能用父节点的线性数量来表达。
-
其它逻辑程序设计方法
随机逻辑程序设计(SLPs)(Muggleton,1996;Cussens,1999)是逻辑程序设计和对数线性模型的组合。毕奇和马葛尔顿(2003)阐明了SLPs是KBMC的特殊形式,因此可以用同样的方法转化为马尔科夫逻辑网。和马尔科夫逻辑网一样,SLPs每个句子有个系数,但它们不代表谓词的分布而是Prolog证明树的分布;后者需要边际化求得。与SLPs相似的有很多讨论,如独立选择逻辑(Poole,1993)和PRISM(Sato和Kameya,1997)。
MACCENT是一个有一阶逻辑特征的对数线性学习模型;每个特征是一个类和一个Prolog查询(空头部的语句)的合取。MACCENT和马尔科夫逻辑网主要不同在于MACCENT是一个分类系统(也就是根据属性预测一个对象的类的条件分布),而马尔科夫逻辑网代表了谓词集全部联合分布。和其它概率近似方法一样,只要给出适当的条件查询,马尔科夫逻辑网就能简单地用来进行分类。特别的,一个MACCENT模型只要定义一个类谓词(第8章第1节),加入相应的特性和权重,再加上权重无穷大的一条规则表明每个对象必须有一个类别,就能简单地转换为马尔科夫逻辑网。(这将无法求得没有类型的谓词的边缘分布,如果仅仅为了回答分类查询,那么就没有问题。)MACCENT能使用以Prolog语句表示的确定的背景知识,这些可以通过为马尔科夫逻辑网增加权重无穷大的相应规则在马尔科夫逻辑网中实现。另外,马尔科夫逻辑网还允许不确定的知识(通过有限权重的规则实现),如第8章第1节,马尔科夫逻辑网能用来进行集合分类,那样不同对象的类型还可以相互依赖;而MACCENT做不到,因为每个对象需以不同的Prolog知识库表示。
受限逻辑程序设计(CLP)是逻辑程序设计的扩展,它的变量在推理时不绑定特定值而是受限(Laffer和Lassez,1987)。概率CLP将SLPs一般化为CLP(Riezler,1998),而CLP(BN)在CLP中结合了贝叶斯网络(Santo Costa等,2003)。和马尔科夫逻辑网不同的是,CLP(BN)中的约束是硬约束(也就是它们不能被冲突;幸好定义了概率分布形式)。
-
概率关系模型
概率关系模型(PRMs)(Friedman等,1999)是框架结构和贝叶斯网络的结合。PRMs可通过为每个类属性(命题的或关系的)定义一个谓词S(x,v)(意思是“对象x的属性S值为v”),写出每个规则(类级别的)条件概率表和子节点属性来转变成马尔科夫逻辑网。而规则是描述父节点状态的字和描述子节点状态的字的合取,权重是P(x|Parent(x))(CPT表中对应的条目)的对数。另外马尔科夫逻辑网可带有权重无穷大的规则以表示必须是某个值的属性。上述所有的方法可解决PRMs中的所有不确定性(属性、引用和存在的不确定性)。
正如塔斯卡等(2002)指出的,PRMs中不能有环的要求极大增加了它的表达能力和计算难度。PRMs的推理需要构建全部的基本网络,这使得它的规模大大受限。PRMs要求确定每个类的每个属性的条件模型,这在复杂的规模大的领域负担很重。相反,马尔科夫逻辑网就为用户需要的一阶逻辑特性创建全部的联合分布。
-
关系马尔科夫网
关系马尔科夫网(RMNs)使用数据库查询作为团模板,每个团的状态都有一个特性(Taskar等,2002)。马尔科夫逻辑网比RMNs更一般化,提供了一种更强大的语言来表述特性(用一阶逻辑替代了查询的合取),还提供了任意关系间的不确定性(不仅仅是对象个体的属性)。RMNs以团数量的指数增长,而马尔科夫逻辑网允许用户(或学习者)来确定特性的数量,这使得它能适应团规模的增加。RMNs采用了不公平的训练方法,所以不能完全确定域中变量的联合分布。马尔科夫逻辑网的差别训练很简单(实际上比本文用的一般训练法简单),我们已经用投票感知算法初步试验成功(Collins,2002)。RMNs使用最大后验概率和信仰传播来推理,虽然设置了差别,但是还是相当慢;查询变量的最大拟似然方法可能更加有效。
-
结构化逻辑回归
在结构化逻辑回归(SLR)(Popescul和Ungar,2003)中,判断结果是输入数据的SQL查询结果。就像一个逻辑回归模型是差别训练的马尔科夫网一样,一个SLR模型就是一个差别训练的马尔科夫逻辑网。
-
关系依赖网络
在一个关系依赖网络(RDN)中,每个节点在马尔科夫毛毯下的条件概率由一个决策树得出(Neville和Jensen,2003)。就象每个依赖网都有相应的马尔科夫网一样,在用吉布斯采样得到平稳分布后,每个RDN都有相对应的马尔科夫逻辑网。
-
板块和概率实体关系模型
有许多重复结构的大型图模型常常能用板块间接地表示(Buntine,1994)。马尔科夫逻辑网蕴含了板块的表达方法,另外,它允许个体和它们之间的关系被显式表示(Cussens,2003);上下文相关的独立性被紧凑表示,而不是隐藏在节点模型中。最近,赫克曼等(2004)结合了板块和概率实体关系特点基础上提出一种新语言,这种语言是马尔科夫逻辑网的一个特例,就和实体关系是逻辑的特例一样。概率实体关系模型能让逻辑表达式约束基本网络的搭建,但是必须先知道这些表达式的真假值,而马尔科夫逻辑网允许所有逻辑表达式的不确定性。
-
BLOG
米尔希等(2004)提出了一种语言,叫做BLOG,目的是摆脱命名唯一性和范围封闭性假设。一个BLOG程序定义了如何产生一个事件的过程,这样很难与任意的一阶逻辑知识库相结合,它仅定义了模型结构,参数则需要通过外部调用来确定;还有BLOG模型是有向图,需要避免环路产生,这实质上增加了它的设计复杂度。第4章已经讲述了如何在马尔科夫逻辑网中去除命名唯一性和范围封闭性假设(如果有未知对象属于多种类型,那么,就为每个类型产生一个随机变量),推导对象的属性而不是它们的观测值就可以使用对象的变量而不是它们的观测值简单实现(比如,“书”和它们的引用一样)。据我们所知,BLOG目前还没有被应用和评估。
-
其它
统计关系学习领域中还有许多研究我们没有提到,本章仅简要介绍了与马尔科夫逻辑网潜在相关的一些工作。
Pasula和Russell(2001)、Poole(2003)、Sanghai等(2003)研究了一阶逻辑模型推理的效率问题,虽然只要集中在有向图模型上,但某些想法(比如,不同类型谓词采用不同的MCMC步骤、将合一与变量剔除组合起来、抽象层次)可以被应用到马尔科夫逻辑网上。
马尔科夫逻辑网和KBANN系统有一些有趣的相似之处,它们都会将一个命题的霍恩知识库转化为一个神经网络再用后向传播学习权重(Towell和Shavlik,1994),更一般来说,马尔科夫逻辑网可看作知识密集性学习一系列工作在概率估算上的扩展。
下一步研究计划
马尔科夫逻辑网是一个有潜力的解决众多很多人工智能问题的工具,但仍有许多工作要做。今后工作的方向集中在以下三个主要领域:
推理:我们计划为马尔科夫逻辑网开发更有效的MCMC方法;研究信仰传播的使用;鉴别和利用有用的特殊案例;调查提升推理的可能性。
学习:我们计划修订学习算法;用直接优化(伪)法改良马尔科夫逻辑网的结构;研究重量学习的替代方法;研究马尔科夫逻辑网的差别训练;研究如何从不完整的数据中学习;将马尔科夫逻辑网用于基于链接的集群;研究概率谓词的发现方法。
应用:我们想在多个领域应用马尔科夫逻辑网,包括信息提取和集成、自然语言处理、视觉、社会网络分析、计算机生物学等。
总结
马尔可夫逻辑网络(MLNs)是一种在有限领域将一阶逻辑和概率结合起来的简单方法。一个马尔科夫逻辑网通过一阶逻辑知识库的规则(或条款)的权重来获得,可看作构建一般马尔科夫网络的模板,知识库中每个可能的基本规则都会产生一个特性。推理需对回答查询所需最小子集进行基本化,再由MaxWalkSat确定初始状态,然后通过吉布斯采样法对这个子网进行采样来实现。权重是通过使用L-BFGS算法的优化拟似然法学习的,而规则我们使用CLAUDIEN系统来学习。大学领域的真实世界数据的测试结果显示了马尔科夫逻辑网的前景。马尔科夫逻辑网学习和推理的源代码可在链接源代码中找到。