数据结构-----基于双数组的Trie树

Trie树简介

Trie树也称字典树，在字符串的查找中优势比较明显，适用于在海量数据中查找某个数据。因为Trie树的查找时间和数据总量没有关系，只和要查找的数据长度有关。比如搜索引擎中热度词语的统计。除此之外也可用于将数据按字典序排序。
另外Trie树是典型的空间换时间的数据结构，构建一颗Trie树需要花费比较大的内存空间。

简单的Trie树的实现有两种方式，每个节点存储一个子节点数组，或者用链表将每个节点的子节点连接起来。
采用数组浪费了大量的空间，因为在Trie树使用的过程中不可能整个树是满的，所以数组中绝大多数的位置都是空闲的，空间得不到有效利用，但是因为数组支持随机访问，所以查找时效率很高
采用链表虽然节省了不少空间，但是在查找的过程中难以高效定位。

为了将两者的优点有效地结合起来，出现了一种仅用两个线性数组描述的Trie树，称为双数组Trie树（DAT）。两个数组分别是base和check，理解它们的含义是学习DAT的关键。

base数组和check数组

base和check数组用于记录节点和节点之间的关系，而自身的数据是通过在数组中的索引表示的。上文提到的Trie树为每个节点都开辟一定大小的数组来存储孩子节点，但是开辟的大小是事先规定好的，只能处理比如说英文单词这种简单的数据，而对于中文的处理不是很理想，双数组Trie树将每个数据都映射成一个整型数，既是数据的编码又可用于在base和check数组中定位索引。

双数组Trie树中只有树结构意义上的节点，并无实际的表述，而节点与节点之间的关系仅是通过base和check记录的。

编码
在理解base和check数组之前，先了解一下有关编码的事情。计算机在存储数据时都是以二进制的形式存储的，
比如想要存储字符’a’，并不是直接将’a’放入内存，而是将其转换成对应的编码（一个整型数97），随后进行进制转换存储在内存中。想要存储中文”一”，也是需要要将其转换成对应的编码（19968），然后再进行存储。
所以可以理解成，任何数据都有唯一的整数值与其对应，这就是数据的编码。目前比较流行的就是Unicode码，可以有效处理中文字符。

起始索引begin
有了编码的知识，首先想到的是将每个数据转换成对应的Code，然后这个Code就是这个数据在base和check中的下标。但是没办法维护节点之间的关系，不过也不能说这种想法是错的，至少对了一部分。原因是在base和check中的下标不是只由Code组成，还需要一个起始索引begin，这个begin是在程序中需要计算的整数（目前先假设begin以求出）。
这个起始索引begin很像HashTable中的hash地址，在哈希表中，对于每个数据，都有一个确定的哈希散列函数将这个数据转换成一个整数，这个整数就是数据在哈希表中的索引。
而对于双数组而言，begin + Code组成了某个数据在base和check中的下标。

base数组
但是你可能会问，这样也没有父节点子节点的关系？
这就是base要解决的事情，考虑一下，每个数据都有一个唯一的begin作为它的起始索引，这个begin就好比于是数据的归属地。父节点有，孩子节点也同样有，那么就可以利用base数组来存储数据的孩子节点的起始索引child_begin。也就是说，base[begin + code] = child_begin，这样，在知道父节点的编码，和父节点的起始索引begin后，就能找到它的孩子节点的起始索引child_begin，然后child_begin + child_code就是孩子节点在base和check数组中的下标。

你可能又会问，父节点会有多个孩子节点，而base中只存储了一个begin？
具有相同父节点的节点之间互为兄弟关系，只需要保证兄弟节点具有相同的起始索引begin就可以了，对吗。

check数组
而对于check数组，它存储的值是每个数据的起始索引begin，也就是说
check[begin + code] = begin。它的作用在于判断某个数据是否存在，比如说现在知道了父节点的begin和code，想要判断父节点有没有表示某个数据的孩子节点，这个数据的编码为child_code，那么就可以先求出父节点的孩子们的起始索引child_begin（利用base数组就可以了，child_begin = base[begin + code]）。求出之后考虑，如果那个数据存在，那么它就是父节点的孩子，它的起始索引就是child_begin，那么它的check数组中存储的就应该是child_begin。所以可以根据
check[child_begin + child_code]是否等于child_begin来判断是否存在这个数据。

初始化操作

以下面的数据为例，任务是将这些数据放入Trie树中。

//如下数据
一举
一举一动
一举成名
一举成名天下知
万能
万能胶

每个字的编码如下：

胶     名     动     知    下    成    举    一    能    天    万    
33014 21517 21160 30693 19979 25104 20030 19968 33021 22825 19975

中文的编码一般都比较大（小于65536），所以在创建一棵双数组Trie树时，需要为base和check开辟很大的内存。又因为begin的值也有可能很大，所以仅仅开辟65536是远远不够的。
先考虑上面的问题，应该采用什么方法将这些数据添加到树中，换言之就是放入base和check数组中呢。

根据base的含义，兄弟节点之间具有相同的起始索引begin，所以在添加的过程中，每次添加的节点们是互为兄弟的关系。

起始索引begin的选择
对于互为兄弟的几个数据，假设他们的编码是a1,a2,a3,…,an。选择begin的依据是需要满足：

check[begin + a1] = 0;
check[begin + a2] = 0;
check[begin + a3] = 0;
    ...
check[begin + an] = 0；

check数组的赋值
初始化时check中的元素都为0，表示没有位置被占用，check[i]不为0表示i这个索引位置已经被其他的数据占用了，需要重新为这些兄弟数据找begin。而找到满足上述条件的begin之后，需要将这些数据的check赋值为他们的起始索引begin，表示对应索引位置已经被占用。

check[begin + a1] = begin;
check[begin + a2] = begin;
check[begin + a3] = begin;
    ...
check[begin + an] = begin;

base数组的赋值
而base数组在什么时候赋值呢，base数组存储的是孩子们的起始索引child_begin，也就是说需要在为孩子们找到child_begin之后才能将父节点的base设置成child_begin。即

base[begin + code] = child_begin；

又因为初始化操作是从根节点开始的，所以很显然需要利用递归的思想。

举例
在上面的例子中，互为兄弟的字如下：

"一","万"     父节点为根节点
"举"         父节点为"一"
"null", "一", "成"    父节点为"举"
"动"         父节点为"一"
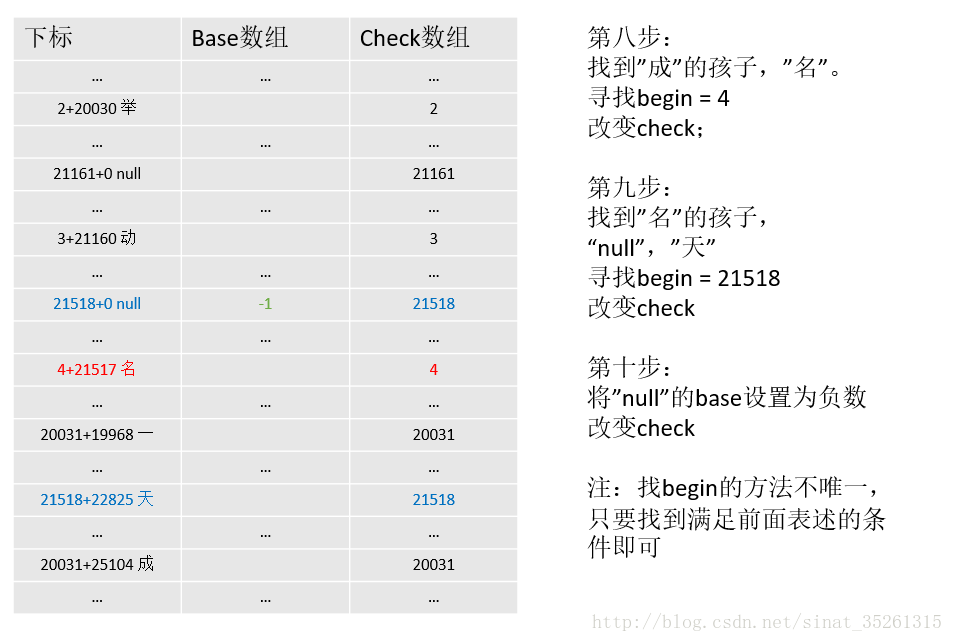
"名"         父节点为"成"
...
"能"         父节点为"万"
...

注意在计算兄弟节点时会多计算一个”null”，表示叶子节点，标识从根节点到它的父节点为止表示的数据是一个完整的词，也就是”一举”是一个词。
不同于其他的数据节点，子结点的编码为0，在base中的值需要设为负数，在判断是否存在某个词时，需要利用这个负值判断。
比如说，想要判断”一举”是否在词典中，只需要找到”举”的孩子们的起始索引child_begin后，判断base[child_begin + 0]是否是负数即可。
那在插入数据的过程中怎么判断哪个节点是叶子结点呢。考虑一下，在插入数据的时候，每次都需要为某个数据生成它的孩子数据（像为”举”找到”null”,”一”,”成”一样），而叶子结点没有孩子数据，所以可以根据找到的孩子是否为空进行判断。

初始时，为根节点的base和check赋值。根节点的下标为0，base[0]表示孩子们的起始索引，初始化时设置为1.

base[0] = 1;
check[1] = 0;

初始化操作流程：

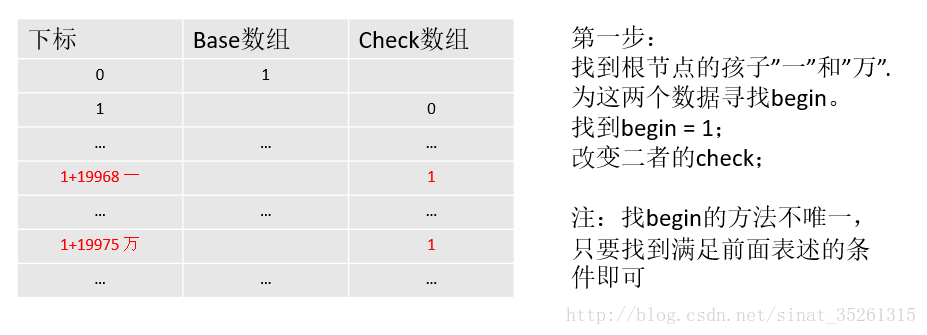
1. 先选取第一批互为兄弟的节点，”一”和”万”。
2. 为它们寻找一个满足条件的起始索引begin1，并改变二者的check.
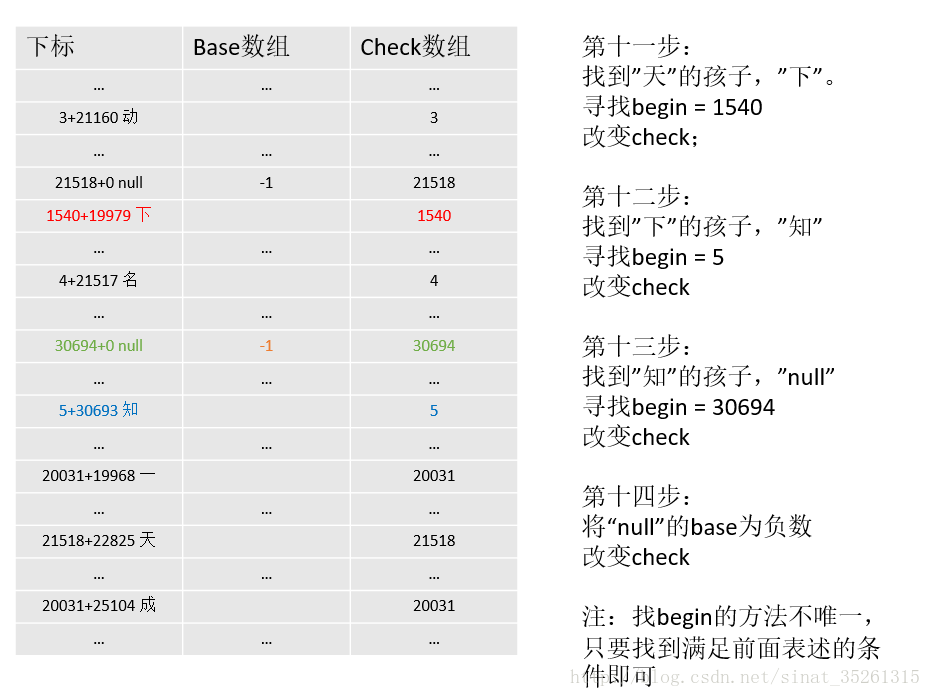
3. 找到”一”的孩子”举”。
4. 为”举”寻找满足条件的起始索引begin2，并改变check。
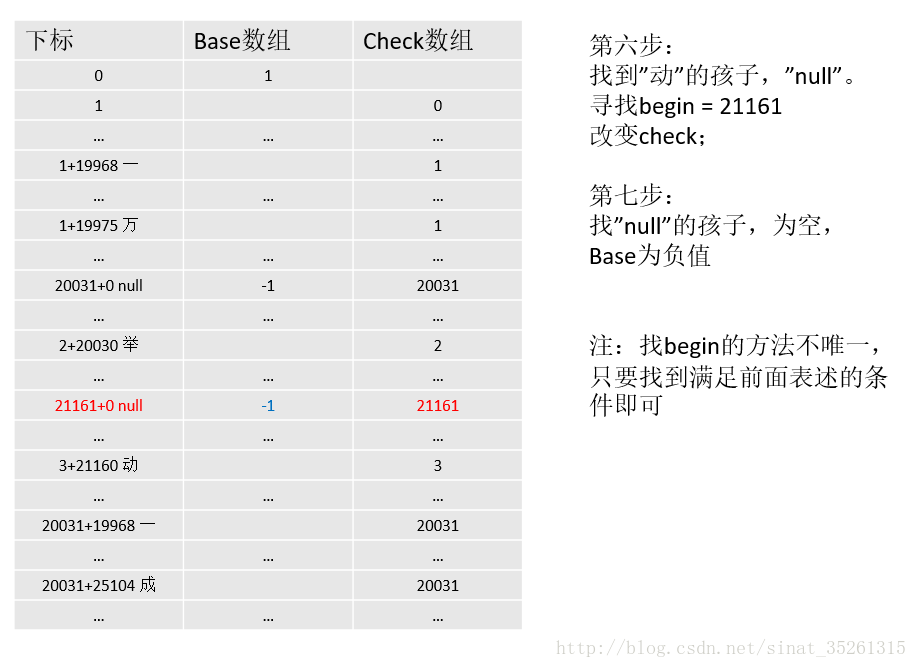
5. 找”举”的孩子们”null”,”一”,”成”。
6. 为孩子们找到满足条件的起始索引begin3。
7. 找”null”的孩子，没有找到，将”null”的base赋值为负数
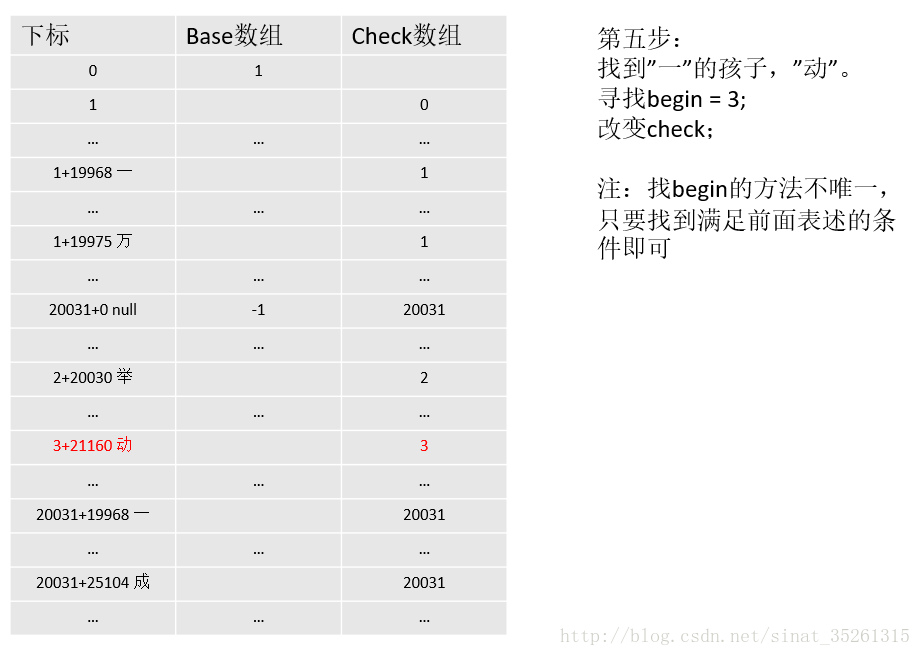
8. 找”一”的孩子”动”。
9. ….
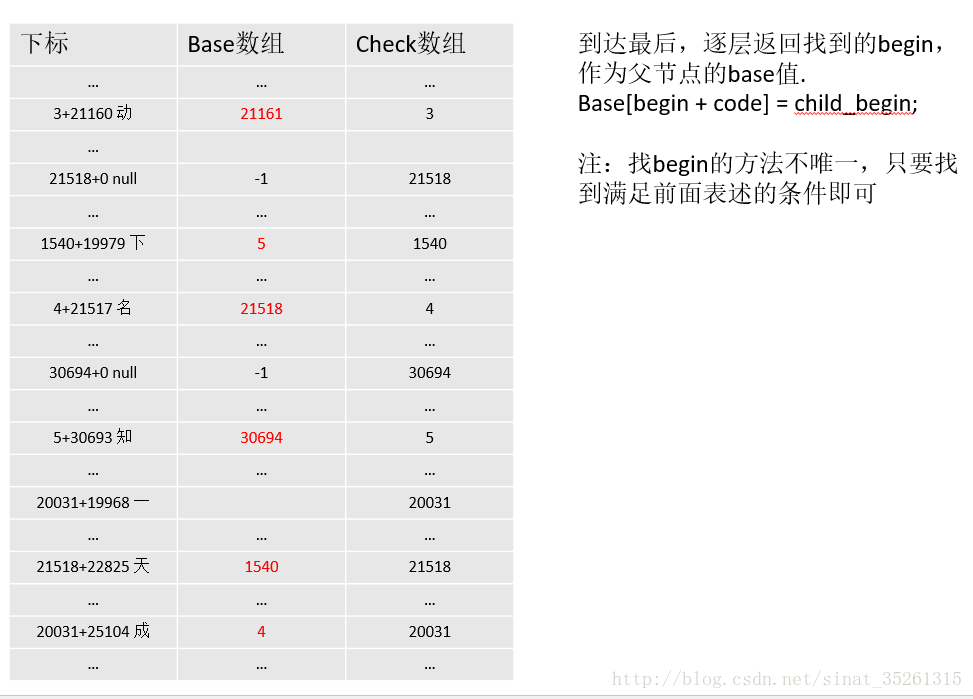
10. 当找到最后的，递归到最后一层时，向上返回每次寻找的begin。
11. ….
12. 将”举”的base设置为begin3，将”一”的base设置为begin2，将”0”的base设置为begin1。
13. 然后再为”万”字进行同样的操作。
14. …

查询操作

整个流程下来，所有的数据都在base和check中存储。对于查询操作，比如说给定一个词语，需要判断这个词语是否在Trie树表示的词典中，步骤如下：
1. 计算begin1（base[0])
2. 计算第一个字的编码code1
3. 判断第一个字是否存在，check[begin1 + code1] == begin1表示存在
4. 若存在，将begin赋值为第二个字的起始索引，begin2 = base[begin1 + code1]
5. 计算第二个字的编码code2
6. 判断第二个字是否存在，check[begin2 + code2] == begin2表示存在
7. 若存在，将begin赋值为第三个字的起始索引，begin3 = base[begin2 + code2]
8. …
9. 当全部遍历后，beginN表示最后一个字的孩子们的起始索引。判断base[beginN + 0] <
0是否成立，成立就表示存在，否则表示不存在。

注：只要有一处check[begin + code] != begin就表示不存在，返回fasle

流程示例

下面以

一举 
一举一动 
一举成名 
一举成名天下知 
万能 
万能胶

为例，进行初始化操作的说明。

每个字的编码如下：

胶     名     动     知    下    成    举    一    能    天    万    
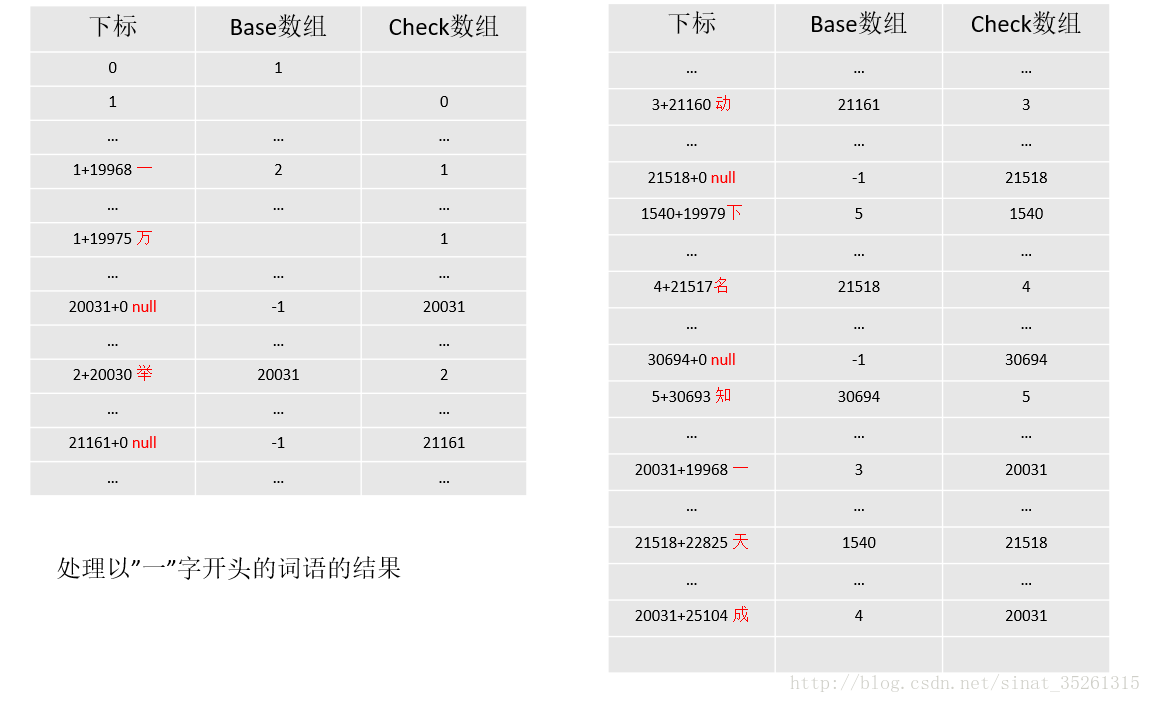
33014 21517 21160 30693 19979 25104 20030 19968 33021 22825 19975

在处理完以”一”字开头的词语后，继续处理以”万”字开头的词语。如果词典中词语有很多，则依次处理。
需要考虑的函数有

1. 找到以某个字作为前缀字的字，比如说处理完”举”字，需要寻找”举”的孩子”null”，”一”，”成”。
2. 为互为兄弟关系的几个字寻找满足条件的起始索引begin。然后递归地进行步骤1。当遇到叶子节点时，将叶子节点的base设置成负数。每层递归返回本层的begin作为父节点的base值。

参考的博客
http://www.hankcs.com/program/java/%E5%8F%8C%E6%95%B0%E7%BB%84trie%E6%A0%91doublearraytriejava%E5%AE%9E%E7%8E%B0.html