蚁群算法
一种应用于组合优化问题的启发式搜索算法。蚁群算法是一种用来寻找优化路径的概率型算法
组合优化：
组合优化（Combinatorial Optimization）问题的目标是从组合问题的可行解集中求出最优解，通常可描述为：令Ω={s1，s2，…，sn}为所有状态构成的解空间，C(si)为状态si对应的目标函数值，要求寻找最优解s*，使得对于所有的si∈Ω，有C(s*)=minC(si)。组合优化往往涉及排序、分类、筛选等问题，它是运筹学的一个重要分支。
来自
蚁群算法在解决离散组合优化方面具有良好的性能。
一、基本思想
1、蚂蚁觅食：
信息素跟踪：按照一定的概率沿着信息素较强的路径觅食。
信息素遗留：会在走过的路上会释放信息素，使得在一定的范围内的其他蚂蚁能够觉察到并由比影响它们的行为。
2、归结为几点：
（1）环境：有障碍物、有其他蚂蚁、有信息素
（2）觅食规则：范围内寻找是否有食物，否则看是否有信息素，每只蚂蚁都会以小概率犯错，
（3）移动规则：都朝信息素最多的方向移动，无信息素则继续朝原方向移动，且有随机的小的扰动，有记忆性。
（4）避障规则：移动的方向如有障碍物挡住，蚂蚁会随机选择另一个方向
（5）信息素规则：越靠近食物播撒的信息素越多，越离开食物播撤的信息素越少。
根据以上规则，模拟一个算法，即蚁群算法
二、蚁群算法
1、应用：
旅行商问题 & TSP问题：有n个城市，从起点 0 开始游历每一个城市，只访问每个城市一次，最后回到起点，所需要的最短路径是多少？ （ACM中使用状压DP来解决问题）
这个属于NP完全问题。最直接的方法就是枚举法，解空间为n个元素的所有排列组合，为(n−1)!。n稍微一大就无法在有限的时间内做出。
蚂蚁搜索食物的过程：
通过个体之间的信息交换与相互协作，最终找到从蚁穴到食物源的最短路径。
2.模型
蚂蚁k在运动过程中，根据各条路径上的信息素决定转移方向。
3.蚁群系统的模型：
：表示在t时刻蚂蚁 k 选择从元素(城市) x 转移到元素(城市) y 的概率，也称为随机比例规则。
α值越大，该蚂蚁越倾向于选择其他蚂蚁经过的路径，该状态转移概率越接近于贪婪规则。
α=0 不再考虑信息素水平，算法就成为有多重起点的随机贪婪算法
β=0 算法就成为纯翠的正反馈启发式搜索。
- 补充（启发式搜索）：
启发式算法（heuristic algorithm)是相对于最优化算法提出的。一个问题的最优算法求得该问题每个实例的最优解。启发式算法可以这样定义：一个基于直观或经验构造的算法，在可接受的花费（指计算时间和空间）下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度一般不能被预计。现阶段，启发式算法以仿自然体算法为主，主要有蚁群算法、模拟退火法、神经网络等。
-------------------------------------------------------------------------------第二天接上-------------
用参数1-ρ表示信息素消逝程度，蚂蚁完成一次循环，各路径上信息素浓度消散规则为：
蚁群的信息素浓度更新规则为：
M. Dorigo给出的三种不同模型：
1、蚂蚁圈系统（效果最好，通常作为蚁群优化算法的基本模型）：
- 利用的是全局信息 ，即蚂蚁完成一个循环后，更新所有路径上的信息。
2、蚂蚁数量系统：
利用的是局部信息 ，即蚂蚁每走一步都要更新残留信息素的浓度。
3、蚂蚁密度系统：
利用的是局部信息 ，即蚂蚁每走一步都要更新残留信息素的浓度。
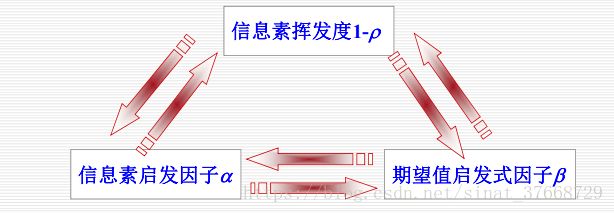
三、算法参数选择
1、信息素启发因子（α）
Ø 反映了蚁群在路径搜索中随机性因素作用的强度；
Ø α值越大，蚂蚁选择以前走过的路径的可能性越大，搜索的随机性减弱；
Ø 当α 过大时会使蚁群的搜索过早陷于局部最优。
2、期望值启发式因子（β）
Ø 反映了蚁群在路径搜索中先验性、确定性因素作用的强度；
Øβ 值越大，蚂蚁在某个局部点上选择局部最短路径的可能性越大；
Ø 虽然搜索的收敛速度得以加快，但蚁群在最优路径的搜索过程中随机性减弱，易于陷入局部最优。
3、信息素挥发度 1-ρ
Ø 当要处理的问题规模比较大时，会使那些从来未被搜索到的路径(可行解)上的信息量减小到接近于0，因而降低了算法的全局搜索能力；
Ø 而且当1-ρ过大时，以前搜索过的路径被再次选择的可能性过大，也会影响到算法的随机性能和全局搜索能力；
Ø 反之，通过减小信息素挥发度 1-ρ虽然可以提高算法的随机性能和全局搜索能力，但又会使算法的收敛速度降低。
