『经典DP入门』LCS 最长公共子序列问题

最长公共子序列问题（Longest Common Subsequence problem）：给定两个序列X = 和Y = ，求X和Y长度最长的公共子序列。

注：本文的大多数概念及求解方法来自《算法导论》

---

使用动态规划求解LCS问题过程：

一、刻画最长公共子序列的特征

LCS的最优子结构定理：设X={x1，x2，……，xm}和Y={y1，y2，……，yn}为两个序列，并设Z={z1、z2、……，zk}为X和Y的任意一个LCS，则：

        （1）如果xm=yn，那么zk=xm=yn，而且Zk-1是Xm-1和Yn-1的一个LCS。

　　 （2）如果xm≠yn，那么zk≠xm蕴含Z是是Xm-1和Yn的一个LCS。

　　 （3）如果xm≠yn，那么zk≠yn蕴含Z是是Xm和Yn-1的一个LCS。

这个定理也很好理解，有一些减而治之的思想，举个栗子：

从字符串的最后一位开始比较

1.对 X = "AGTGATG",Y = "GTTAG",则Z = "GTAG"，此时m = 7，n = 5，k = 4（从1开始）。

比较X和Y最后一位，x7 = y5，同时删去，Xm-1 = "AGTGAT"，Yn-1 = "GTTA"，Zk-1 = "GTA"。我们可以发现，Zk-1就是Xm-1和Yn-1的一个LCS。

2.对 X = "AGTGAT",Y = "GTTA",则Z = "GTA"，此时m = 6，n = 4，k = 3（从1开始）。

比较最后一位，x6 ≠ y4，z3  ≠ x6 ，Xm-1 = "AGTGA"，Z是Xm-1和Yn的一个LCS。

3.将2的X和Y互换即可

对 Y = "AGTGAT",X = "GTTA",则Z = "GTA"，此时n = 6，m = 4，k = 3（从1开始）。

比较最后一位，x4 ≠ y6，z3  ≠ x4 ，Yn-1 = "AGTGA"，Z是Xm和Yn-1的一个LCS。

此 定理说明两个序列的一个LCS也包含两个序列的前缀的一个LCS，即LCS问题具有最优子结构性质。

二、一个递归解

从一中可以得到一个结论，在求X = 和Y = 的一个LCS时，我们需要求解一个或两个子问题。如果xm = yn,我们应该求解xm-1和yn-1的一个LCS，如果xm ≠ yn，我们必须求解两个子问题：xm-1和yn的一个LCS 和 xm和yn-1的一个LCS。两个较长者应该为xm和yn的一个LCS。

可以总结为以下的公式：

i 和 j 可以认为两个串的长度

『朴素递归版本代码』

#include 
#include 
#include 
using namespace std;
int ans;
string X,Y;
int solve(int i,int j){
	int cnt = 0;
	if(i == -1 || j == -1) return 0;
	if(X[i] == Y[j]){
		cnt = solve(i-1,j-1)+1;
	}else{
		cnt = max(solve(i,j-1),solve(i-1,j));
	}
	return cnt;
}
int main(){

	cin>>X>>Y;
	int len1 = X.length(),len2 = Y.length();
	ans = solve(len1-1,len2-1);
	cout<<"ans = "<

三、动态规划计算LCS的长度

 采用动态规划自底向上计算解。以两个序列为输入。将计算序列的长度保存到一个二维数组dp[M][N]中。M和N分别表示两个序列的长度。该过程代码如下：

#include 
#include 
#include 
#include 
using namespace std;
string X,Y;
int dp[200][200];
int main(){
	cin>>X>>Y;
	int len1 = X.length(),len2 = Y.length();
	for(int i = 1; i <= len1; i++){
		dp[i][0] = 0;
		dp[0][i] = 0;
	}
	for(int i = 1; i <= len1; i++){
		for(int j = 1; j <= len2; j++){
			if(X[i-1] == Y[j-1])
					dp[i][j] = dp[i-1][j-1]+1;
			else
				dp[i][j] = max(dp[i][j-1],dp[i-1][j]); 
			
		}
	}
	cout<<"   ";
	for(int i = 1; i <= len2; i++){
		cout<<" "<
 
  
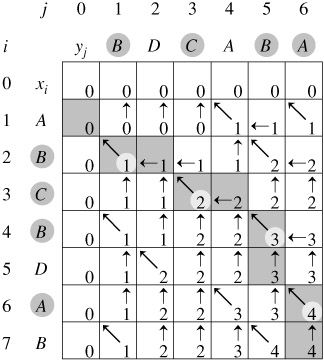
算法导论中给出的记录结果