神经网络之激活函数

激活函数的主要作用能使得神经网络的每层输出结果变得非线性化。神经网络加入激活函数之后，才能进行非线性映射。

目录

激活函数的性质：

sigmoid

tanh

ReLu

Leaky ReLU

ELU 指数线性函数

Maxout

Softmax激活函数

激活函数的选择 

---

激活函数的性质：

1可微性：计算梯度时必须要有此性质。

2非线性：保证数据非线性可分。

3单调性：保证凸函数。

4输出值与输入值相差不会很大：保证神经网络训练和调参高效

神经网络常用的激活函数

 

sigmoid

                             

导数=s(x)(1-s(x))

sigmoid函数把输出的实数压缩到0-1之间，一般形式g（z）=1/(1+exp(-z)),z为输出结果

当z很大时，g（z）约为1，z很小（负无穷时），g（z）约为0，输出的数值可以当作分类的概率，比如在二分类中，激活函数的输出为0.9的话便可以解释为90%的概率为正样本。

左侧软饱和：

右侧软饱和：

    与软饱和相对的是硬饱和激活函数，即：f‘(x)=0，当 |x| > c，其中 c 为常数。

    同理，硬饱和也分为左侧硬饱和和右侧硬饱和。常见的ReLU 就是一类左侧硬饱和激活函数。

Sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体来说，由于在后向传递过程中，sigmoid向下传导的梯度包含了一个f‘(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f‘(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。

优点： 输出在[0,1]之间， 直观，适合前向传播
缺点：1Sigmoid函数饱和使梯度消失。当神经元的激活在接近0或1处时会饱和，在这些区域梯度几乎为0，这就会导致梯度消失，几乎就有没有信号通过神经传回上一层，导致权重更新很慢，梯度消失
2非0均值输出。这会引入一个问题，当输入均为正值的时候，由于f = sigmoid(wTx+b)),那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。

3计算量大，都将把时间放在exp和矩阵点乘上了

tanh

                  数学表达式         

              导数为                        

                 图形为
                     

优点  tanh输出是0均值的，实际应用中，tanh函数比Sigmoid函数更好，收敛速度比sigmoid快

缺点：没解决sigmoid的梯度弥散问题

 

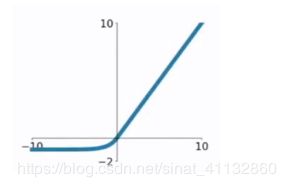
ReLu

全称Rectified Linear Units

数学表达式               y=max(0,x)

全区间不可导

                              

优点

1计算简单。相比于 sigmoid/tanh，ReLU 只需要一个阈值就可以得到激活值

 2 应用于SGD算法时，收敛速度比 sigmoid 和 tanh 快

3解决了梯度消失问题，适用于后向传播

缺点：

1、输出不是0均值的

2、ReLU没有对数据做幅度压缩，数据的幅度会随着模型层数的增加不断增大

3、可能出现神经元坏死现象。（上述梯度弥散问题）某些神经元可能永远不会被激活，导致相应参数永远不会被更新（因为在负数部分，梯度为0）。

造成这样原因是初始权重设置糟糕或者学习率过高，解决办法是设置了一个合适的较小的learning rate，那么发生的可能性变小。

Leaky ReLU

用来解决Relu带来的神经元坏死问题，但是表现并不一定比Relu好

函数形式为，其中可以设为0.01

图形如下，（x,y只是个变量，不用在意这些细节）

 

                                 

ELU 指数线性函数

数学形式：  

图形为：           

                      

优点：具有Relu的优点，且不会有dead relu问题，且输出的均值接近于0

缺点： 计算量大，且表现不一定比ReLU好

Maxout

Maxout是深度学习网络中的一层网络，maxout 可以认为是网络的激活函数层。

maxout过程：假设某层输入是X=（x1,x2,……xd），

Maxout隐藏层第i个神经元的计算公式：

公式中的计算公式为：

maxout隐藏层w权重为d*m*k ，b的权重为m*k  d为输入层向量维度，m为隐藏层神经元个数，k为输出层个数，如果k=1，那么就类似与MLP多层感知机。maxout干的事情是隐藏层同时训练k组参数，然后选择激活值最大的作为下一层神经元的激活值。

栗子如下：

为简化起见，以MLP为例，第i层输入为两个，第i+1层输出为1个，

                                                 

传统的MLP计算的公式为

                                                             z=W*X+b

                                                              out=f(z)

式子中f是激活函数，如sigmod、Relu、Tanh等。

而在maxout中

                         

看到隐藏层不是固定的函数形式（如sigmoid这样的），隐藏层在输入输出层之间多加了一层，也就是多加了k个神经元，隐藏层的计算公式为 :                         

                      z1=w1*x+b1

                     z2=w2*x+b2

                      z3=w3*x+b3

                       z4=w4*x+b4

                       z5=w5*x+b5

                       h(x)=max(z1,z2,z3,z4,z5)

可以看到，加入maxout层之后，多了k倍的参数

优点：

1maxout的拟合能力是非常强的，它可以拟合任意的的凸函数

2具有ReLU的优点。没有ReLU的如神经元的死亡的缺点。

3maxout是一个可学习的激活函数，因为W参数是学习变化的

缺点：

每个神经元中有两组(w,b)参数，参数个数成k倍增加

Softmax激活函数

        Softmax是另一种Sigmoid函数，但是它是在分类中比较容易控制的一种激活函数。Sigmoid只能处理两类的问题。Softmax将输出结果压缩在0-1之间，并依据输出的总和来分类。

                    Softmax数学形式：

                                                       

           例如输入为   x=[1,2,3,4]，输出为 [0.0320586 , 0.08714432, 0.23688282, 0.64391426]     

softmax非线性映射采用了指数函数，目的是尽量拉大向量中大小分量之间的差距 

 

激活函数的选择 

• Sigmoid函数以及它们的联合通常在分类器的中有更好的效果
• 由于梯度崩塌的问题，在某些时候需要避免使用Sigmoid和Tanh激活函数
• ReLU函数是一种常见的激活函数，在目前使用是最多的
• 如果遇到了一些死的神经元，我们可以使用Leaky ReLU函数
• ReLU永远只在隐藏层中使用
• 根据经验，一般可以从ReLU激活函数开始，但是如果ReLU不能很好的解决问题，再去尝试其他的激活函数

reference：https://blog.csdn.net/shwan_ma/article/details/76252355

                   https://blog.csdn.net/zchang81/article/details/70224688

                   《Maxout  Networks》

                 http://www.datalearner.com/blog/1051508750742453

Chinese (Simplified)English

Chinese (Simplified)English

 

Options : History : Feedback : Donate

Close