图信号处理之图拉普拉斯矩阵的含义
目录
- 图信号也可以看作图函数
- 拉普拉斯算子 = 梯度的散度
- 图信号的梯度
- 图信号的梯度的散度
- 图拉普拉斯矩阵
- 图拉普拉斯矩阵在图信号中的应用
- 【参考资料】
图拉普拉斯矩阵 L L L定义为图的度矩阵 D D D减去图的(加权)邻接矩阵 W W W。这一定义来自谱图论,在图信号处理理论中也非常常见。然而,图拉普拉斯矩阵为什么如此定义?它有什么含义?它与经典信号处理中的拉普拉斯算子有什么关系?这篇博文致力于回答关于图拉普拉斯矩阵的这几个问题。
本文将解释图信号的梯度和散度的定义,给出图拉普拉斯矩阵的另一个定义,并最终解释 L = D − W L=D-W L=D−W的含义。为了便于理解,本文将以一个图信号的例子贯穿始终。
图信号也可以看作图函数
图信号是一种描述非结构化数据的数据表示形式。经典的数字信号处理的处理对象是时间信号,由一系列不同时间的采样点组成。这其中暗含着一种非常规则的数据结构,即每个采样点都按照时间顺序规则排列。然而,实际中我们常常需要处理非规则结构的数据,这些数据不仅包括本身的数值信息,还包括数据之间的结构关联信息。例如,交通网络,无线传感器网络,社交网络等等。图信号打破了经典数字信号处理的规则结构局限,致力于处理图结构上的信号。
例如我们关注如下图信号。
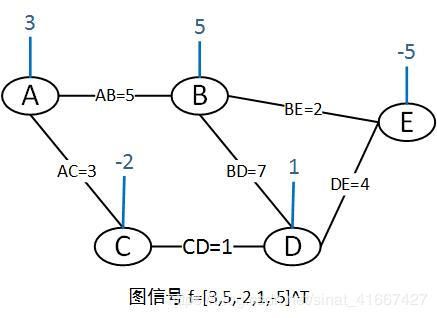
这个图信号由向量 f = [ 3 , 5 , − 2 , 1 , − 5 ] T \boldsymbol{f}=[3,5,-2,1,-5]^T f=[3,5,−2,1,−5]T表示。与经典数字信号不同的是,这个图信号向量依托于特定的图 G = { V , E , W } \mathcal{G}=\{\mathcal{V},\mathcal{E},W\} G={V,E,W},其中 V = { A , B , C , D , E } \mathcal{V}=\{A,B,C,D,E\} V={A,B,C,D,E}为节点集合, E = { A B , A C , B D , C D , D E , B E } \mathcal{E}=\{AB,AC,BD,CD,DE,BE\} E={AB,AC,BD,CD,DE,BE}为边集合, W W W为图的邻接矩阵。
W = ( 0 5 3 0 0 5 0 0 7 2 3 0 0 1 0 0 7 1 0 4 0 2 0 4 0 ) W=\left(\begin{array}{ccccc} 0 & 5 &3 & 0 & 0 \\ 5 & 0 & 0 & 7 & 2 \\ 3 & 0 & 0 & 1 & 0 \\ 0 & 7 & 1 & 0 & 4 \\ 0 & 2 & 0 & 4 & 0 \end{array}\right) W=⎝⎜⎜⎜⎜⎛0530050072300100710402040⎠⎟⎟⎟⎟⎞
以上即为图信号的表示方法。
下面我们解释本节的标题:图信号也可以看做图函数。
函数可以理解为由定义域向值域的映射。图信号与之相同,可以看作由节点域向实数域的映射 γ : V → R \gamma:\mathcal{V} \rightarrow\mathbb{R} γ:V→R,即每个节点对应一个实数值。本例子中,映射 γ \gamma γ: 节点 A → 3 A \rightarrow3 A→3, 节点 B → 5 B \rightarrow5 B→5, 节点 C → − 2 C \rightarrow-2 C→−2, 节点 D → 1 D \rightarrow1 D→1, 节点 E → − 5 E \rightarrow-5 E→−5.
由于本文主要关注图上的拉普拉斯算子,这是一个函数上的概念,因此接下来我们使用“图函数”这个名词。需要注意的是,这里的“图函数”就是“图信号”,只是在本文中我们不再区分这两个概念。
拉普拉斯算子 = 梯度的散度
对于函数 g ( x , y , z ) g(x,y,z) g(x,y,z)来说,将拉普拉斯算子 ∇ 2 \nabla^2 ∇2作用于函数 g ( x , y , z ) g(x,y,z) g(x,y,z),就等价于求函数 g ( x , y , z ) g(x,y,z) g(x,y,z)的梯度的散度。
函数 g ( x , y , z ) g(x,y,z) g(x,y,z)为标量函数,其梯度为矢量场 ∇ g = ∂ g ∂ x ⋅ i ⃗ + ∂ g ∂ y ⋅ j ⃗ + ∂ g ∂ z ⋅ k ⃗ \nabla g=\frac{\partial g}{\partial x} \cdot \vec{i}+\frac{\partial g}{\partial y} \cdot \vec{j}+\frac{\partial g}{\partial z} \cdot \vec{k} ∇g=∂x∂g⋅i+∂y∂g⋅j+∂z∂g⋅k, 其中每个点处的矢量都表示函数 g ( x , y , z ) g(x,y,z) g(x,y,z)在该点的梯度,方向指向函数在此点变化最快的方向,大小表示变化的快慢。
对梯度 ∇ g \nabla g ∇g求散度,得到标量场,表示每个点处的梯度矢量是发散还是汇聚,散度为负值则表示此处的函数梯度矢量向内汇聚,散度为正值则表示此处的函数梯度矢量向外发散。 ∇ ⋅ ∇ g = ∇ 2 g \nabla\cdot\nabla g=\nabla^2 g ∇⋅∇g=∇2g,此处的 ∇ 2 \nabla^2 ∇2就被称为拉普拉斯算子。
总结起来,拉普拉斯算子即为求函数的梯度的散度。
为了解释图拉普拉斯矩阵,我们首先关注图信号的梯度,再关注图信号梯度的散度。
图信号的梯度
图信号理论中的许多概念都由经典数字信号处理推广获得。因此,为了获得图函数的梯度,我们首先回顾经典函数的梯度,并将其推广至图函数中。
经典函数 g ( x , y , z ) g(x,y,z) g(x,y,z)的梯度为 ∇ g = ∂ g ∂ x ⋅ i ⃗ + ∂ g ∂ y ⋅ j ⃗ + ∂ g ∂ z ⋅ k ⃗ \nabla g=\frac{\partial g}{\partial x} \cdot \vec{i}+\frac{\partial g}{\partial y} \cdot \vec{j}+\frac{\partial g}{\partial z} \cdot \vec{k} ∇g=∂x∂g⋅i+∂y∂g⋅j+∂z∂g⋅k,描述的是函数 g ( x , y , z ) g(x,y,z) g(x,y,z)在 i ⃗ , j ⃗ , k ⃗ \vec{i},\vec{j},\vec{k} i,j,k三个方向的变化(即偏导数)。我们关注 x x x方向, ∂ g ∂ x = lim d → 0 g ( x + d x ) − g ( x ) ( x + d x ) − x \frac{\partial g}{\partial x}=\lim_{d\rightarrow 0} \frac{g(x+d x)-g(x)}{(x+d x)-x} ∂x∂g=limd→0(x+dx)−xg(x+dx)−g(x).
由此推广至图信号。我们定义图信号的每个边都有一个梯度值,为 γ ( v ) − γ ( u ) d v u = ( γ ( v ) − γ ( u ) ) ⋅ w v u \frac{\gamma(v)-\gamma(u)} {d_{vu}}=(\gamma(v)-\gamma(u))\cdot w_{vu} dvuγ(v)−γ(u)=(γ(v)−γ(u))⋅wvu. 注意,图信号的梯度是针对边的,图信号在每条边上都有一个梯度值。这里蕴含的含义是,图函数认为每个边都是一个正交的方向。
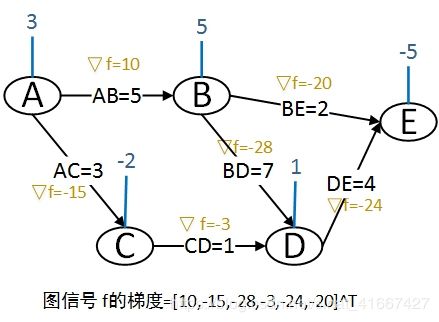
我们计算一下前面所述图信号例子 f = [ 3 , 5 , − 2 , 1 , − 5 ] T \boldsymbol{f}=[3,5,-2,1,-5]^T f=[3,5,−2,1,−5]T的梯度,每条边的梯度都是边两端端点信号值之差乘上权值。
f \boldsymbol{f} f在边 A B AB AB方向上的梯度 = ( 5 − 3 ) × 5 = 10 =(5-3)\times5=10 =(5−3)×5=10;
f \boldsymbol{f} f在边 A C AC AC方向上的梯度 = ( − 2 − 3 ) × 3 = − 15 =(-2-3)\times3=-15 =(−2−3)×3=−15;
f \boldsymbol{f} f在边 B D BD BD方向上的梯度 = ( 1 − 5 ) × 7 = − 28 =(1-5)\times7=-28 =(1−5)×7=−28;
f \boldsymbol{f} f在边 C D CD CD方向上的梯度 = ( − 2 − 1 ) × 1 = − 3 =(-2-1)\times1=-3 =(−2−1)×1=−3;
f \boldsymbol{f} f在边 D E DE DE方向上的梯度 = ( − 5 − 1 ) × 4 = − 24 =(-5-1)\times4=-24 =(−5−1)×4=−24;
f \boldsymbol{f} f在边 B E BE BE方向上的梯度 = ( − 5 − 5 ) × 2 = − 20 =(-5-5)\times2=-20 =(−5−5)×2=−20;
即, ∇ f = [ 10 , − 15 , − 28 , − 3 , − 24 , − 20 ] T \nabla \boldsymbol{f}=[10,-15,-28,-3,-24,-20]^T ∇f=[10,−15,−28,−3,−24,−20]T.
这里可以理解为,图信号 f \boldsymbol{f} f在边 A B AB AB上的偏导值为10,在边 A C AC AC上的偏导值为-15,边 A B AB AB是增长趋势,边 A C AC AC是下降趋势,且边 A C AC AC的下降趋势比边 A B AB AB快。
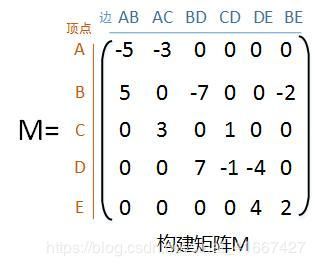
上述运算可以通过矩阵运算实现。我们构造矩阵 M M M,每行代表一个顶点,每列代表一个边,每个元素为对应边的权值。可以看出,矩阵 M M M的每列仅有两个非零元素,它们互为相反数,标示着这条边的两个端点。这里需要说明的是,每列所示的边在一个端点处为正值,一个端点处为负值,这个安排可以是任意的,并不会影响最终的拉普拉斯矩阵的值。例如,矩阵 M M M的第一列是 [ − 5 , 5 , 0 , 0 , 0 ] T [-5,5,0,0,0]^T [−5,5,0,0,0]T,即我们在构造矩阵 M M M时认为边 A B AB AB由端点 A A A指向端点 B B B。如果把矩阵 M M M的第一列写成 [ 5 , − 5 , 0 , 0 , 0 ] T [5,-5,0,0,0]^T [5,−5,0,0,0]T,即让边 A B AB AB反向,这种构造方式也是正确的,最终计算出的拉普拉斯矩阵不会变化。
在矩阵 M M M的帮助下,我们可以用矩阵运算实现图信号的梯度运算和散度运算。
我们取邻接矩阵 W W W的转置矩阵,记为矩阵 T = W T T=W^T T=WT。则上述梯度运算等价于矩阵运算: ∇ f = T × f \nabla \boldsymbol{f}=T\times \boldsymbol{f} ∇f=T×f,矩阵 T T T即为图信号的梯度算子。
( − 5 5 0 0 0 − 3 0 3 0 0 0 − 7 0 7 0 0 0 1 − 1 0 0 0 0 − 4 4 0 − 2 0 0 2 ) × ( 3 5 − 2 1 − 5 ) = ( 10 − 15 − 28 − 3 − 24 − 20 ) \left(\begin{array}{ccccc} -5 & 5 & 0 & 0 & 0 \\ -3 & 0 & 3 & 0 & 0 \\ 0 & -7 & 0 & 7 & 0 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & -4 & 4 \\ 0 & -2 & 0 & 0 & 2 \end{array}\right) \times\left(\begin{array}{c} 3 \\ 5 \\ -2 \\ 1 \\ -5 \end{array}\right)=\left(\begin{array}{c} 10 \\ -15 \\ -28 \\ -3 \\ -24 \\ -20 \end{array}\right) ⎝⎜⎜⎜⎜⎜⎜⎛−5−3000050−700−2030100007−1−40000042⎠⎟⎟⎟⎟⎟⎟⎞×⎝⎜⎜⎜⎜⎛35−21−5⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎜⎛10−15−28−3−24−20⎠⎟⎟⎟⎟⎟⎟⎞
图信号的梯度的散度
仍然沿用上一节的思路,将经典函数中的概念推广至图函数中。经典函数中,矢量场的散度定义为该点处的通量。图函数的定义域为离散的节点域,每个节点处的散度即定义为该点处射入的矢量减去该点处射出的矢量。注意,图信号的梯度的散度是针对节点的,每个节点有一个散度值。
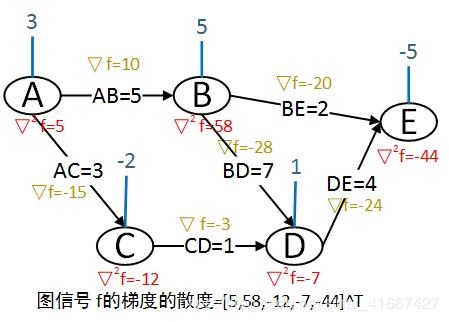
我们计算一下前面所述图信号例子 f = [ 3 , 5 , − 2 , 1 , − 5 ] T \boldsymbol{f}=[3,5,-2,1,-5]^T f=[3,5,−2,1,−5]T的梯度 ∇ f = [ 10 , − 15 , − 28 , − 3 , − 24 , − 20 ] T \nabla \boldsymbol{f}=[10,-15,-28,-3,-24,-20]^T ∇f=[10,−15,−28,−3,−24,−20]T的散度,每个点的散度都是该点处射入的梯度矢量减去该点处射出的梯度矢量。即,每个点射出的梯度矢量当作负值,射入的梯度矢量当作正值。该点散度为所有矢量的加和。注意,这里对于无向图的边赋予的方向,即为前面构造矩阵 M M M时赋予的方向。
f \boldsymbol{f} f在点 A A A处的梯度的散度= ( − 1 ) × ( − 15 ) + ( − 1 ) × 10 = 5 (-1)\times(-15)+(-1)\times10=5 (−1)×(−15)+(−1)×10=5;
f \boldsymbol{f} f在点 B B B处的梯度的散度= 1 × 10 + ( − 1 ) × ( − 20 ) + ( − 1 ) × ( − 28 ) = 58 1\times10+(-1)\times(-20)+(-1)\times(-28)=58 1×10+(−1)×(−20)+(−1)×(−28)=58;
f \boldsymbol{f} f在点 C C C处的梯度的散度= 1 × ( − 15 ) + ( − 1 ) × ( − 3 ) = − 12 1\times(-15)+(-1)\times(-3)=-12 1×(−15)+(−1)×(−3)=−12;
f \boldsymbol{f} f在点 D D D处的梯度的散度= 1 × ( − 28 ) + − 1 × ( − 3 ) + ( − 1 ) × ( − 24 ) = − 7 1\times(-28)+-1\times(-3)+(-1)\times(-24)=-7 1×(−28)+−1×(−3)+(−1)×(−24)=−7;
f \boldsymbol{f} f在点 E E E处的梯度的散度= 1 × ( − 20 ) + − 1 × ( − 24 ) = − 44 1\times(-20)+-1\times(-24)=-44 1×(−20)+−1×(−24)=−44;
即, ∇ 2 f = [ 5 , 58 , − 12 , − 7 , − 44 ] T \nabla^2 \boldsymbol{f}=[5,58,-12,-7,-44]^T ∇2f=[5,58,−12,−7,−44]T.
这里可以理解为,点 A A A处既有边 A B AB AB方向上值为-10的变化趋势,又有边 A C AC AC方向上值为15的变化趋势,综合起来,点 A A A处的变化程度是5;点 B B B处既有边 A B AB AB方向上值为10的变化趋势,又有边 B D BD BD方向上值为28的变化趋势,又有边 B E BE BE方向上值为20的变化趋势,综合起来,点 B B B处的变化程度是58. 58 > 5 58>5 58>5, 即点 B B B处的变化程度比点 A A A更剧烈。
上述运算也可以在邻接矩阵 W W W的帮助下实现。我们构建矩阵 S S S,其每个元素与邻接矩阵相应元素的正负号相同,大小只取1. 则求梯度的散度运算等价于矩阵运算: ∇ 2 f = S × ∇ f = S × T × f \nabla^2\boldsymbol{f}=S\times\nabla\boldsymbol{f}=S\times T\times\boldsymbol{f} ∇2f=S×∇f=S×T×f。
( − 1 − 1 0 0 0 0 1 0 − 1 0 0 − 1 0 1 0 − 1 0 0 0 0 1 1 − 1 0 0 0 0 0 1 1 ) × ( 10 − 15 − 28 − 3 − 24 − 20 ) = ( 5 58 − 12 − 7 − 44 ) \left(\begin{array}{cccccc} -1 & -1 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & 0 & 0 & -1 \\ 0 & 1 & 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \end{array}\right) \times\left(\begin{array}{c} 10 \\ -15 \\ -28 \\ -3 \\ -24 \\ -20 \end{array}\right)=\left(\begin{array}{c} 5 \\ 58 \\ -12 \\ -7 \\ -44 \end{array}\right) ⎝⎜⎜⎜⎜⎛−11000−101000−101000−110000−110−1001⎠⎟⎟⎟⎟⎞×⎝⎜⎜⎜⎜⎜⎜⎛10−15−28−3−24−20⎠⎟⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎛558−12−7−44⎠⎟⎟⎟⎟⎞
图拉普拉斯矩阵
通过前述图信号的梯度的散度的运算可以知道,图拉普拉斯矩阵 L = S × T L=S\times T L=S×T。
我们计算上述例子中的 L L L:
L = S × T = ( 8 − 5 − 3 0 0 − 5 14 0 − 7 − 2 − 3 0 4 − 1 0 0 − 7 − 1 12 − 4 0 − 2 0 − 4 6 ) L=S\times T=\left(\begin{array}{cccccc} 8 & -5 & -3 & 0 & 0 \\ -5 & 14 & 0 & -7 & -2 \\ -3 & 0 & 4 & -1 & 0 \\ 0 & -7 & -1 & 12 & -4 \\ 0 & -2 & 0 &-4 & 6 \end{array}\right) L=S×T=⎝⎜⎜⎜⎜⎛8−5−300−5140−7−2−304−100−7−112−40−20−46⎠⎟⎟⎟⎟⎞
可以看出,该图的拉普拉斯矩阵在数值上等于 D − W D-W D−W。
L = D − W = ( 8 − 5 − 3 0 0 − 5 14 0 − 7 − 2 − 3 0 4 − 1 0 0 − 7 − 1 12 − 4 0 − 2 0 − 4 6 ) L=D-W=\left(\begin{array}{cccccc} 8 & -5 & -3 & 0 & 0 \\ -5 & 14 & 0 & -7 & -2 \\ -3 & 0 & 4 & -1 & 0 \\ 0 & -7 & -1 & 12 & -4 \\ 0 & -2 & 0 &-4 & 6 \end{array}\right) L=D−W=⎝⎜⎜⎜⎜⎛8−5−300−5140−7−2−304−100−7−112−40−20−46⎠⎟⎟⎟⎟⎞
通常情况下,由于矩阵减法比矩阵乘法运算复杂度低,所以常常见到的图拉普拉斯矩阵定义为 L = D − W L=D-W L=D−W,而实际上,图拉普拉斯矩阵的另一个定义是 L = S × T L=S\times T L=S×T,这个定义包含着梯度的散度这一物理含义。
另外,补充一点。图拉普拉斯矩阵只用于描述无向图,不能描述有向图。有向图的邻接矩阵不是对称矩阵,也不存在拉普拉斯矩阵的定义。虽然在构造矩阵 M M M以及计算梯度和散度的过程中似乎是给每条无向图的边赋予了方向,但这个方向是任意赋予的,而且在最终的拉普拉斯矩阵中也没有体现出来。可以这样理解,在计算梯度和散度时,我们任意选择了一个坐标系(边的方向),来衡量图函数的变化程度。计算完图信号的梯度的散度后,我们发现无论如何选择坐标系都会得到相同的结果,所以我们抛弃了坐标系,获得了绝对结果(即无向图的拉普拉斯矩阵)。
图信号处理中,对于图谱有多种定义,如邻接矩阵谱,拉普拉斯谱,无符号拉普拉斯谱(也称为Q-谱),距离谱等等。这些图谱定义各有优缺点,拉普拉斯谱具有很多优良性质,但只能描述无向图,这是它的局限之一。
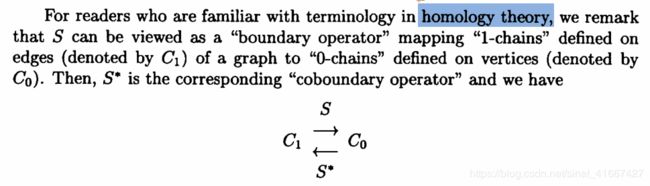
最后,补充《谱图论》这本书中对于前述矩阵 M M M的说明。书中1.2节提到的矩阵 S S S即为本文中的矩阵 M M M。矩阵 M M M可以看作是同调论中的“边界算子”。
图拉普拉斯矩阵在图信号中的应用
为什么谱图论和图信号处理总是专注于图拉普拉斯矩阵?这是因为图拉普拉斯矩阵能够描述图的变化程度,能够定义图的频率。而且,图拉普拉斯矩阵还有一些其他的优良性质,比如,
- 拉普拉斯矩阵的 n n n个特征值都是非负值。由于拉普拉斯矩阵的行和恒为零,所以其最小特征值也恒为零。而且,有 0 = λ 1 ≤ λ 2 ≤ … ≤ λ n 0=\lambda_{1} \leq \lambda_{2} \leq \ldots \leq \lambda_{n} 0=λ1≤λ2≤…≤λn。图信号的频率即定义来源于此,图信号的频率值即为图拉普拉斯矩阵的特征值。
例如,对前述图拉普拉斯矩阵进行特征值分解,可得
L = U Γ U T L=U\Gamma U^T L=UΓUT
U = ( 0.4472 0.2817 0.6189 0.4992 − 0.2974 0.4472 − 0.1614 0.3548 − 0.3059 0.7446 0.4472 0.7167 − 0.5156 − 0.1151 0.0852 0.4472 − 0.2946 0.0162 − 0.6052 − 0.5888 0.4472 − 0.5424 − 0.4743 0.5270 0.0563 ) U=\left(\begin{array}{ccccc} 0.4472 &0. 2817 & 0.6189 & 0.4992 & -0.2974 \\ 0.4472 &-0.1614 &0.3548 & -0.3059 & 0.7446 \\ 0.4472 &0. 7167&-0.5156 & -0.1151 & 0.0852 \\ 0.4472 & -0.2946 & 0.0162 &-0.6052 & -0.5888 \\ 0.4472 & -0.5424 &-0.4743 &0.5270 & 0.0563 \end{array}\right) U=⎝⎜⎜⎜⎜⎛0.44720.44720.44720.44720.44720.2817−0.16140.7167−0.2946−0.54240.61890.3548−0.51560.0162−0.47430.4992−0.3059−0.1151−0.60520.5270−0.29740.74460.0852−0.58880.0563⎠⎟⎟⎟⎟⎞
Γ = ( 0 0 0 0 0 0 3.2321 0 0 0 0 0 7.6327 0 0 0 0 0 11.7550 0 0 0 0 0 21.3803 ) \Gamma=\left(\begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 \\ 0 & 3.2321 &0 & 0 & 0 \\ 0 & 0 &7.6327 & 0& 0 \\ 0 & 0 & 0 & 11.7550& 0 \\ 0 & 0 & 0 & 0 & 21.3803 \end{array}\right) Γ=⎝⎜⎜⎜⎜⎛0000003.2321000007.63270000011.75500000021.3803⎠⎟⎟⎟⎟⎞ - 图拉普拉斯矩阵是半正定实对称矩阵。因为是实对称矩阵所以特征向量相互正交, 可以构成图谱域的正交基,而且特征值向量组成的矩阵 U U U为正交矩阵,有 U − 1 = U T U^{-1}=U^T U−1=UT;又因为半正定,其特征值均为非负实数(如上一条)。
- 拉普拉斯矩阵的特征值有一些很好的实际含义。例如,最小非零特征值是图的代数连通度;特征值中0出现的次数就是图连通区域的个数。
- 矩阵 L L L与 h h h的瑞利熵为 R ( L , h ) = h ∗ L h h ∗ h R(L, h)=\frac{h^{*} L h}{h^{*} h} R(L,h)=h∗hh∗Lh。瑞利熵的最大值等于 L L L的最大特征值,瑞利熵的最小值等于 L L L的最小特征值。图信号的带宽定义即来源于此。
【参考资料】
- https://www.kechuang.org/t/84022?page=0&highlight=859356
- https://ieeexplore.ieee.org/document/7979524
- https://ieeexplore.ieee.org/document/8254798
- 《Spectral Graph Theory》