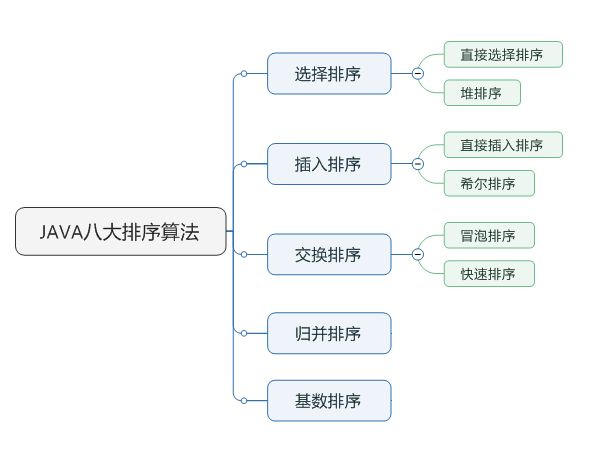
JAVA八大排序算法
最近面试招人,感觉自己的智商秀逗了,强化训练,强化原理记忆,跑通多种思路不混乱
https://github.com/singgel/eight-sorting-algorithms
选择排序---直接选择排序
选择排序包括两种,分别是直接选择排序和堆排序,选择排序的基本思想是每一次在n-i+1(i=1,2,3,...,n-1)个记录中选取键值最小的记录作为有序序列的第i个记录,首先我们来看选择排序中的第一种排序---直接选择排序。直接选择排序的基本思想是,在第i次选择操作中,通过n-i次键值间比较,从n-i+1个记录中选出键值最小的记录,并和第i(1小于等于1小于等于n-1)个记录交换,说了基本思想之后,赶脚还是稀里糊涂的,我们来看一下直接选择排序具体是如何排序的,如下图所示:‘
![]()
如上所示的一组序列为8、5、2、6、9、3、1、4、0、7,首先我们在这个里面选取一个最小的数当然最大的也可以,具体根据要求来进行选择,我们以从小到大的顺序进行排列,首先,我们选取一个最小的数字0,0和8进行交互位置,经过第一次选择之后,序列的顺序变成0、5、2、6、9、3、1、4、8、7,接着进行第二次选择,再选择一个最小的数字1,1和5交互位置,依次类推,直到该序列是有序序列为止。
public static void main(String[] args) {
int [] s = {8,5,2,6,9,3,1,4,0,7};
int temp = 0;
for(int i=0;is[j]){
temp=j; //保存位置
}
}
if(temp!=i) exchang(s,i,temp); //进行交换
}
for(int value:s)
System.out.print(value);
}
private static void exchang(int[] s, int i, int j) {
int temp = s[j];
s[j]=s[i];
s[i]=temp;
} 选择排序---堆排序
接着我们来看选择排序中的另一种排序---堆排序,由上面的直接选择排序分析,我们知道,在n个键值中选出最小值,至少进行n-1次比较,然而继续在剩余的n-1个键值中选择出第二个小的值是否一定要进行n-2次比较呢?如果能利用钱n-1次比较所得信息,是否可以减少以后各次选中的次数比较呢?基本这个,我们来看堆排序,堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法,利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值,即A[PARENT[i]] >= A[i]。在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的要求可知,最大的值一定在堆顶。我们来看堆排序到底是怎么排的呢?下面我们以小堆为例,如下图所示:
![]()
如上图所示的序列是6、5、3、1、8、7、2、4,我们首先将其构建成一个堆,通过构建我们发现这个时候的序列为8、6、7、4、5、3、2、1,接着,我们1和8进行比较,发现1小于8,所以交互位置,刨去8,这个时候的序列为1、6、7、4、5、3、2,发现7比1大,交互位置,1比3小,交互位置,构成的是一个大顶堆了,这个时候,只需要7跟二叉树的最后一个节点进行比较即可,刨去7,依次类推,这里用语言描述的不是很准确,没有立体感,很难进行想象,小伙伴可以仔细看上面的这个动态图是如何进行堆排序的。
public static void main(String[] args) {
int[] array = { 6, 5, 3, 1, 8, 7, 2, 4 };
System.out.println("排序前:");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + ",");
}
System.out.println();
System.out.println("分割线---------------");
heapSort(array);
System.out.println("排序后:");
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + ",");
}
}
public static void heapSort(int[] array) {
if (array == null || array.length == 1)
return;
buildMaxHeap(array); // 第一次排序,构建最大堆,只保证了堆顶元素是数组里最大的
for (int i = array.length - 1; i >= 1; i--) {
// 这个是什么意思呢?,经过上面的一些列操作,目前array[0]是当前数组里最大的元素,需要和末尾的元素交换
// 然后,拿出最大的元素
swap(array, 0, i);
// 交换完后,下次遍历的时候,就应该跳过最后一个元素,也就是最大的那个值,然后开始重新构建最大堆
// 堆的大小就减去1,然后从0的位置开始最大堆
// maxHeap(array, i, 0);
minHeap(array, i, 0);
}
}
// 构建堆
public static void buildMaxHeap(int[] array) {
if (array == null || array.length == 1)
return;
// 堆的公式就是 int root = 2*i, int left = 2*i+1, int right = 2*i+2;
int cursor = array.length / 2;
for (int i = cursor; i >= 0; i--) { // 这样for循环下,就可以第一次排序完成
// maxHeap(array, array.length, i);
minHeap(array, array.length, i);
}
}
// 最大堆
public static void maxHeap(int[] array, int heapSieze, int index) {
int left = index * 2 + 1; // 左子节点
int right = index * 2 + 2; // 右子节点
int maxValue = index; // 暂时定在Index的位置就是最大值
// 如果左子节点的值,比当前最大的值大,就把最大值的位置换成左子节点的位置
if (left < heapSieze && array[left] > array[maxValue]) {
maxValue = left;
}
// 如果右子节点的值,比当前最大的值大,就把最大值的位置换成右子节点的位置
if (right < heapSieze && array[right] > array[maxValue]) {
maxValue = right;
}
// 如果不相等,说明啊,这个子节点的值有比自己大的,位置发生了交换了位置
if (maxValue != index) {
swap(array, index, maxValue); // 就要交换位置元素
// 交换完位置后还需要判断子节点是否打破了最大堆的性质。最大堆性质:两个子节点都比父节点小。
maxHeap(array, heapSieze, maxValue);
}
}
// 最小堆
public static void minHeap(int[] array, int heapSieze, int index) {
int left = index * 2 + 1; // 左子节点
int right = index * 2 + 2; // 右子节点
int maxValue = index; // 暂时定在Index的位置就是最小值
// 如果左子节点的值,比当前最小的值小,就把最小值的位置换成左子节点的位置
if (left < heapSieze && array[left] < array[maxValue]) {
maxValue = left;
}
// 如果右子节点的值,比当前最小的值小,就把最小值的位置换成左子节点的位置
if (right < heapSieze && array[right] < array[maxValue]) {
maxValue = right;
}
// 如果不相等,说明啊,这个子节点的值有比自己小的,位置发生了交换了位置
if (maxValue != index) {
swap(array, index, maxValue); // 就要交换位置元素
// 交换完位置后还需要判断子节点是否打破了最小堆的性质。最小性质:两个子节点都比父节点大。
minHeap(array, heapSieze, maxValue);
}
}
// 数组元素交换
public static void swap(int[] array, int index1, int index2) {
int temp = array[index1];
array[index1] = array[index2];
array[index2] = temp;
}
插入排序---直接插入排序
常用的插入排序有两种,直接插入排序和希尔排序,首先我们来看直接插入排序,直接插入排序是一种简单的排序方法,她的基本思想是依次将每个记录插入到一个已排好序的有序表中去,从而得到一个新的、记录数增加1的有序表,就好比图书馆整理图书的这么一个过程,接着我们来看一下,直接插入排序的具体排序,如下图所示:
![]()
public static void insertionSort(int[] a) {
int tmp;
for (int i = 1; i < a.length; i++) {
for (int j = i; j > 0; j--) {
if (a[j] < a[j - 1]) {
tmp = a[j - 1];
a[j - 1] = a[j];
a[j] = tmp;
}
}
}
}
public static void main(String[] args) {
int[] a = { 6, 5, 3, 1, 8, 7, 2, 4 };
insertionSort(a);
for (int i : a)
System.out.print(i + " ");
}
如上图所示的一组序列为6、5、3、1、8、7、2、4,首先6和5比较,6比5大交互位置,接着3和5比较,6比3大交互位置,3和5比,交互位置,现在的序列就是3、5、6、1、8、7、2、4,这个时候要把1插入到序列中,首先在徐磊中查找以确定1所应插入的位置,然后就行插入操作,从6起向左顺序查找,由于1小于3,所以1插入的位置就是3的前面,一般情况下,第i(i大于等于1)个记录进行插入操作时,R1、 R2,...,是排好序的有序数列,取出第i个元素,在序列中找到一个合适的位置并将她插入到该位置上即可。
插入排序---希尔排序
基本思想:算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。我们来看下面的一张图,如下所示:
我们来看一个关于希尔排序的例子,如下图所示:
![]()
public static void main(String[] args) {
int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
shellSort(data);
}
public static void shellSort(int[] data) {
// 计算出最大的h值
int h = 1;
while (h <= data.length / 3) {
h = h * 3 + 1;
}
while (h > 0) {
for (int i = h; i < data.length; i += h) {
if (data[i] < data[i - h]) {
int tmp = data[i];
int j = i - h;
while (j >= 0 && data[j] > tmp) {
data[j + h] = data[j];
j -= h;
}
data[j + h] = tmp;
}
}
// 计算出下一个h值
h = (h - 1) / 3;
}
}
希尔排序具体的做法结合上述排序,我们可以很清楚的看出来,先取一个小于n的整数d1作为第一个增量,把序列分为d1个组,即将所有距离为d1倍数序号的记录放在同一个组中,在各组内进行直接插入排序,然后去第二个增量d2,d2小于d1,重复上述分组和排序工具,依次类推,直至所取的增量di=1,即所有记录放在同一组进行直接插入排序为止。
交换排序---冒泡排序
交换排序的基本思想是,比较两个记录键值的大小,如果这两个记录键值的大小出现逆序,则交换这两个记录,这样将键值较小的记录向序列前部移动,键值较大的记录向序列后部移动。首先我们来看交换排序中的第一种排序---冒泡排序,首先将第一个记录的键值和第二个键值进行比较,若为逆序,即R[1].key大于R[2].key,则将这两个记录交换,然后继续比较第二个和第三个记录的键值,依此类推,直到完成第n-1个记录和第n个记录的键值比较交换为止,上述过程称为第一趟起泡,其结果使键值最大的记录移到了第n个位置上,然后再进行第二趟起泡,即对前n-1个记录进行同样的操作,其结果是次大键值的记录安置在第n-1个位置上,重复上面的过程,当在一趟起泡过程中没有进行记录交换的操作时,整个排序过程终止,我们来看下面的一张图:
![]()
public static void main(String[] args) {
int[] arr={6,3,8,2,9,1};
System.out.println("排序前数组为:");
for(int num:arr){
System.out.print(num+" ");
}
for(int i=0;iarr[j+1]){
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
System.out.println();
System.out.println("排序后的数组为:");
for(int num:arr){
System.out.print(num+" ");
}
}
该方法的排序过程与气泡从水中往上冒的情况很相似,所以,美其名曰:冒泡排序,从上图我们可以很清楚的看出来,在排序的过程中,键值较小的记录好比气泡一样向上漂浮,键值较大的记录则向下沉。
交换排序---快速排序
快速排序是交互排序的一种,实质上是对冒泡排序的一种改进,快速排序的基本思想是,在n个记录中取某一个记录的键值为标准,通常取第一个记录键值为基准,通过一趟排序将待排的记录分为小于或等于这个键值的两个独立的部分,这是一部分的记录键值均比另一部分记录的键值小,然后,对这两部分记录继续分别进行快速排序,以达到整个序列有序,我们来看下面的一张图:
![]()
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] a = new int[] { 2, 1, 6, 7, 8, 5, 3, 5 };
quickSort(a, 0, a.length - 1);
System.out.println(Arrays.toString(a));
}
private static void quickSort(int[] a, int begin, int end) {
//
int tbegin = begin, tend = end;
// 将第一个值作为快排序的分界值
int pivot = a[begin];
while (tbegin < tend) {
// 如果两个游标没有交集,或者后面一直大于或等于分界值就一直向前移动
while (tbegin < tend && a[tend] >= pivot) {
--tend;
}
a[tbegin] = a[tend];
// 如果两个游标没有交集,或者前面是小于或等于分界值,就一直向后头移动
while (tbegin < tend && a[tbegin] <= pivot) {
++tbegin;
}
a[tend] = a[tbegin];
}
// 将临界值赋值给游标的交集的地方
a[tbegin] = pivot;
if (begin < tend) {
// 递归排序游标的左边
quickSort(a, begin, tend - 1);
}
if (tbegin < end) {
// 递归排序游标的右边
quickSort(a, tbegin + 1, end);
}
}
归并排序
所谓的归并,是将两个或两个以上的有序文件合并成为一个新的有序文件,归并排序是把一个有n个记录的无序文件看成是由n个长度为1的有序子文件组成的文件,然后进行两两归并,如此重复,直至最后形成包含n个归并,得到n/2个长度为2或者1的有序文件,再两两归并,如此重复,直至最后形成包含n个记录的有序文件位置,这种反复将两个有序文件归并成一个有序文件的排序方法称为二路归并排序。二路归并排序的核心操作是将一堆数组中前后相邻的两个有序序列归并为一个有序序列,如下图所示:
![]()
public static void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high - low + 1];
int i = low;// 左指针
int j = mid + 1;// 右指针
int k = 0;
// 把较小的数先移到新数组中
while (i <= mid && j <= high) {
if (a[i] < a[j]) {
temp[k++] = a[i++];
} else {
temp[k++] = a[j++];
}
}
// 把左边剩余的数移入数组
while (i <= mid) {
temp[k++] = a[i++];
}
// 把右边边剩余的数移入数组
while (j <= high) {
temp[k++] = a[j++];
}
// 把新数组中的数覆盖nums数组
for (int k2 = 0; k2 < temp.length; k2++) {
a[k2 + low] = temp[k2];
}
}
public static void mergeSort(int[] a, int low, int high) {
int mid = (low + high) / 2;
if (low < high) {
// 左边
mergeSort(a, low, mid);
// 右边
mergeSort(a, mid + 1, high);
// 左右归并
merge(a, low, mid, high);
System.out.println(Arrays.toString(a));
}
}
public static void main(String[] args) {
int a[] = { 51, 46, 20, 18, 65, 97, 82, 30, 77, 50 };
mergeSort(a, 0, a.length - 1);
System.out.println("排序结果:" + Arrays.toString(a));
}
基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。我们来看下面的一个例子:
public static void main(String[] args){
//声明要排序的数组
int[] data = {73,22,93,867494,43,55,123,8978,10000,14,28,65,39,81,33,100,567};
//调用基数排序函数
sort(data,10);
//输出排序后的数组
for(int i = 0;i < data.length;i++){
System.out.print(data[i] + " ");
}
}
///基数排序函数
//a表示要排序的数组
//d表示每一位数字的范围(这里是10进制数,有0~9一共10种情况)
public static void sort(int[] a,int d){
//n用来表示当前排序的是第几位
int n = 1;
//hasNum用来表示数组中是否有至少一个数字存在第n位
boolean hasNum = false;
//二维数组temp用来保存当前排序的数字
//第一维d表示一共有d个桶
//第二维a.length表示每个桶最多可能存放a.length个数字
int[][] temp = new int[d][a.length];
int[] order = new int[d];
while(true){
//判断是否所有元素均无比更高位,因为第一遍一定要先排序一次,所以有n!=1的判断
if(n != 1 && !hasNum){
break;
}
hasNum = false;
//遍历要排序的数组,将其存入temp数组中(按照第n位上的数字将数字放入桶中)
for(int i = 0;i < a.length;i++){
int x = a[i]/(n*10);
if(x != 0){
hasNum = true;
}
int lsd = (x%10);
temp[lsd][order[lsd]] = a[i];
order[lsd]++;
}
//k用来将排序好的temp数组存入data数组(将桶中的数字倒出)
int k = 0;
for(int i = 0;i < d;i++){
if(order[i] != 0){
for(int j = 0;j < order[i];j++){
a[k] = temp[i][j];
k++;
}
}
order[i] = 0;
}
n++;
}
}最后还没有完,给大家亲情奉上项目代码:
https://github.com/singgel/eight-sorting-algorithms
我的git上面放了好多这方面的书,希望能帮到你:
https://github.com/singgel/JAVA
https://github.com/singgel/JAVA_LINE
https://github.com/singgel/Study-Floder
附赠树的遍历:
对于节点的定义
class ListNode{
ListNode left;
ListNode right;
int val;
public ListNode(int value){
this.val=value;
}
}
广度优先遍历:
对于广度优先遍历,通过队列这个数据结构可以实现,如下图所示,上面的一行是每次循环队列中的元素,下面的一行是每次遍历的元素。
public void levelOrderTraversal(LsitNode node){
if(node==null){
System.out.print("empty tree");
return;
}
ArrayDeque deque = new ArrayDeque();
deque.add(node);
while(!deque.isEmpty()){
ListNode rnode = deque.remove();
System.out.print(rnode.val+" ");
if(rnode.left!=null){
deque.add(rnode.left);
}
if(rnode.right!=null){
deque.add(rnode.right);
}
}
}
深度优先遍历:上面一行是栈每次循环时保留的数据,每次读只能从最顶端pop()
public void depthTraversal(ListNode node){
if(node==null){
System.out.print("empty tree");
return;
}
Stack stack = new Stack();
stack.push(node);
while(!stack.isEmpty()){
ListNode rnode = stack.pop();
System.out.print(rnode.val);
if(rnode.right!=null){
stack.push(rnode.right);
}
if(rnode.left!=null){
stack.push(rnode.left);
}
}
}