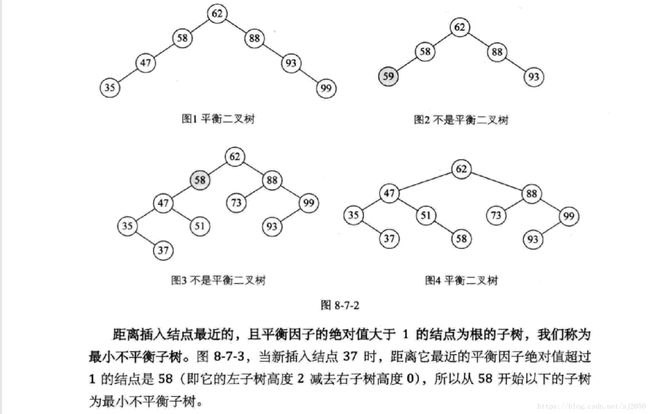
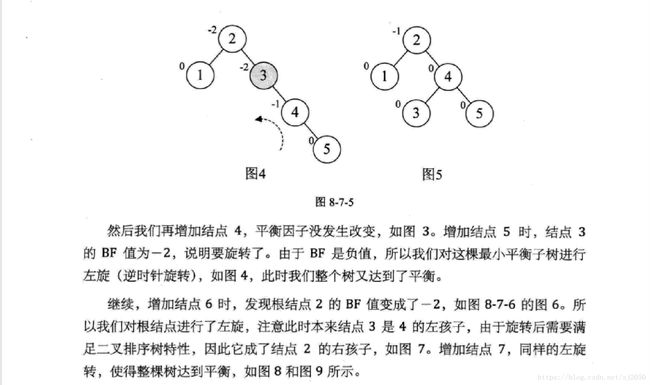
查找——平衡二叉树的实现(代码超详细注释)
既然你搜索到了这篇文章,那么平衡二叉树的作用想必心中已经清楚了,我们接下来就直接来谈谈代码...
目录
知识准备
进阶讲解
代码实现
谢谢阅读
知识准备
啥?你又不知道,真拿你没办法,给你一篇讲的不错的文章:
进阶讲解
喂,看完别走呀,我再讲点进阶的知识,我们知道,平衡二叉树的实现过程中最头疼的就是实现旋转操作,然而,我们可以换一种思维,我们不再去注意旋转这个过程,而直接看重旋转后的结果,旋转后的结果无非是下面这种形式:
即三个节点和四棵子树这种形式,而这里的三个节点分别是失衡节点及其子节点和孙节点(失衡方向上的),四棵子树则为这三个节点的孩子,无论对于左旋操作,右旋操作,左旋-右旋操作,右旋-左旋操作,它们旋转后的结果都可以转化成这种形式,不用考虑旋转的过程大大节省了我们的脑细胞,而这种重构的方式的名字也名如其人——3+4重构。如果对于3+4操作还有疑惑,可以在接下来的代码中理解。
在平衡二叉树中,我们还需要注意,对于节点删除操作,会出现失衡传播现象,即局部失衡你把它重平衡后,它的祖先节点可能又失衡了,所以要我们要不断向上检查是否还有失衡的节点。
代码实现
有了以上的准备,我们就可以上史上最详细注释的代码了:
//BinTree.h
#pragma once
//二叉树模板
//SJ2050
#include
//二叉树节点的模板定义
template
struct BinTreeNode
{
ElemType data; //节点的数据
BinTreeNode *parent; //父节点指针
BinTreeNode *leftChild; //左孩子指针
BinTreeNode *rightChild; //右孩子指针
unsigned int height; //树高
//int bf; //平衡因子,这里为左子树的高度减去右子树的高度(废弃)
};
//二叉树的模板定义
template
class BinTree
{
public:
BinTree(); //构造函数,进行初始化的操作
~BinTree(); //析构函数,进行销毁工作
virtual void Print()=0; //将二叉树中的内容打印出来
virtual BinTreeNode* Search(ElemType data)=0; //搜索节点函数
virtual bool Insert(ElemType data)=0; //插入节点函数
virtual bool Delete(ElemType data) = 0; //删除节点函数
virtual void UpdateHeight(BinTreeNode &node); //更新树高
protected:
BinTreeNode *root; //根节点指针
};
//二叉树构造函数的定义
template
BinTree::BinTree()
{
this->root = nullptr; //将根节点初始化为空
}
//二叉树析构函数的定义
template
BinTree::~BinTree()
{
stack*> stack; //使用STL中的栈
BinTreeNode *p = this->root; //p指针先指向二叉树的根节点
if (p != nullptr)
{
stack.push(p); //将根节点压入栈
while (!stack.empty()) //直至栈中无元素为止
{
p = stack.top(); //p指向栈顶元素
stack.pop(); //栈弹出一个元素,即少一个元素
if (p->leftChild != nullptr)
{
stack.push(p->leftChild); //将左孩子节点压入栈
}
if (p->rightChild != nullptr)
{
stack.push(p->rightChild); //将右孩子节点压入栈
}
delete p; //删除p指向的节点
}
}
this->root = nullptr; //将树的根节点置空
}
//函数功能:更新树中节点的树高
//函数参数:开始更新的节点的引用
//函数返回值:void
template
void BinTree::UpdateHeight(BinTreeNode &node)
{ //该函数自底向上更新各节点的树高
BinTreeNode *p = &node;
while (p != nullptr)
{
if (p->leftChild == nullptr)
{ //当该节点无左孩子时
p->height = p->rightChild == nullptr ? 1 : p->rightChild->height + 1;
}
else if (p->rightChild == nullptr)
{ //当该节点无右孩子时
p->height = p->leftChild == nullptr ? 1 : p->leftChild->height + 1;
}
else
{ //当该节点有左右孩子时
p->height = p->leftChild->height > p->rightChild->height ? \
p->leftChild->height + 1 : p->rightChild->height + 1;
}
p = p->parent; //自底而上更新树高
}
} 以上为二叉树类的模板
//AVL.h
#pragma once
//平衡二叉树模板
//SJ2050
#include "BinTree.h"
#define OK 1
#define FALSE 0
//平衡二叉树类模板定义
template
class AVL : public BinTree
{
public:
void Print(); //将二叉树中的内容打印出来
BinTreeNode* Search(ElemType data); //搜索节点函数
bool Insert(ElemType data); //插入节点函数
bool Delete(ElemType data); //删除节点函数
private:
void Rotate(BinTreeNode &unbalancedNode); //旋转函数
void Connect34(BinTreeNode *a, BinTreeNode *b, BinTreeNode *c,\
BinTreeNode *T0, BinTreeNode *T1, BinTreeNode *T2,\
BinTreeNode *T3); //3+4重构函数
int CalculateBF(BinTreeNode &node); //计算失衡值
void PrintOut(BinTreeNode *beginNode); //采用中序遍历对二叉树进行打印
};
//函数功能:搜索待查找的节点,并返回其位置(供用户调用)
//函数参数:待查找的值
//函数返回值:待查找的节点的指针或该节点应该出现位置的父节点的指针,若树为空返回nullptr
template
BinTreeNode* AVL::Search(ElemType data) //搜索节点函数
{
if (this->root == nullptr)
{ //当树还为空时
return nullptr;
}
BinTreeNode *x = this->root; //x节点
BinTreeNode *p = x->parent; //p为x的父节点
while (x != nullptr && x->data != data )
{
p = x;
if (data > x->data)
{
x = x->rightChild;
}
else
{
x = x->leftChild;
}
}
if (x == nullptr)
{ //当搜索不到要查找的节点时,返回应出现位置的父节点的指针
return p;
}
else
{ //当搜索到要查找的节点时,返回该节点的指针
return x;
}
}
//函数功能:3+4重构实现旋转操作(Private)
//函数参数:三个节点和四棵子树的二级指针
//函数返回值:void
template
void AVL::Connect34(BinTreeNode *a, BinTreeNode *b, \
BinTreeNode *c, \
BinTreeNode *T0, BinTreeNode *T1, \
BinTreeNode *T2, BinTreeNode *T3)
{ //a,c为b的左右孩子,T0,T1,T2,T3又分别为a,c的左右子树
b->leftChild = a;
a->parent = b;
b->rightChild = c;
c->parent = b;
a->leftChild = T0;
if (T0) T0->parent = a; //T0可能为空
a->rightChild = T1;
if (T1) T1->parent = a; //T1可能为空
c->leftChild = T2;
if (T2) T2->parent = c; //T2可能为空
c->rightChild = T3;
if (T3) T3->parent = c; //T3可能为空
//更新三个节点的树高
UpdateHeight(*a);
UpdateHeight(*c);
UpdateHeight(*b);
}
//函数功能:计算节点的失衡值(Private)
//函数参数:要计算的节点的引用
//函数返回值:计算得到的失衡值
template
int AVL::CalculateBF(BinTreeNode &node)
{ //失衡值计算方法为左子树高减去右子树高
int leftTreeHeight = (node.leftChild == nullptr ? 0 : node.leftChild->height); //左子树的高
int rightTreeHeight = (node.rightChild == nullptr ? 0 : node.rightChild->height); //右子树的高
return leftTreeHeight - rightTreeHeight;
}
//函数功能:进行旋转操作(Private)
//函数参数:失衡节点引用
//函数返回值:void
template
void AVL::Rotate(BinTreeNode &unbalancedNode)
{
int bf = CalculateBF(unbalancedNode); //计算出失衡节点的平衡值
if (bf > 0)
{
if (CalculateBF(*unbalancedNode.leftChild) >= 0)
{ //zig型
BinTreeNode *x = unbalancedNode.leftChild->leftChild; //失衡节点的孙节点
BinTreeNode *p = unbalancedNode.leftChild; //失衡节点的子节点
BinTreeNode *g = &unbalancedNode; //失衡节点
//p顶替g的位置
p->parent = g->parent;
if (g->parent != nullptr)
{ //失衡节点有父节点时
if (g->parent->leftChild == g) g->parent->leftChild = p;
else g->parent->rightChild = p;
}
else
{ //失衡节点无父节点时
this->root = p;
}
Connect34(x, p, g, x->leftChild, x->rightChild, p->rightChild, g->rightChild);
}
else
{ //zag-zig型
BinTreeNode *x = unbalancedNode.leftChild->rightChild; //失衡节点的孙节点
BinTreeNode *p = unbalancedNode.leftChild; //失衡节点的子节点
BinTreeNode *g = &unbalancedNode; //失衡节点
//x顶替g的位置
x->parent = g->parent;
if (g->parent != nullptr)
{ //失衡节点有父节点时
if (g->parent->leftChild == g) g->parent->leftChild = x;
else g->parent->rightChild = x;
}
else
{ //失衡节点无父节点时
this->root = x;
}
Connect34(p, x, g, p->leftChild, x->leftChild, x->rightChild, g->rightChild);
}
}
else if (bf < 0)
{
if (CalculateBF(*unbalancedNode.rightChild) <= 0)
{ //zag型
BinTreeNode *x = unbalancedNode.rightChild->rightChild; //失衡节点的孙节点
BinTreeNode *p = unbalancedNode.rightChild; //失衡节点的子节点
BinTreeNode *g = &unbalancedNode; //失衡节点
//p顶替g的位置
p->parent = g->parent;
if (g->parent != nullptr)
{ //失衡节点有父节点时
if (g->parent->leftChild == g) g->parent->leftChild = p;
else g->parent->rightChild = p;
}
else
{ //失衡节点无父节点时
this->root = p;
}
Connect34(g, p, x, g->leftChild, p->leftChild, x->leftChild, x->rightChild);
}
else
{ //zig-zag型
BinTreeNode *x = unbalancedNode.rightChild->leftChild; //失衡节点的孙节点
BinTreeNode *p = unbalancedNode.rightChild; //失衡节点的子节点
BinTreeNode *g = &unbalancedNode; //失衡节点
//x顶替g的位置
x->parent = g->parent;
if (g->parent != nullptr)
{ //失衡节点有父节点时
if (g->parent->leftChild == g) g->parent->leftChild = x;
else g->parent->rightChild = x;
}
else
{ //失衡节点无父节点时
this->root = x;
}
Connect34(g, x, p, g->leftChild, x->leftChild, x->rightChild, p->rightChild);
}
}
}
//函数功能:插入操作(供用户调用)
//函数参数:要插入的节点的数据
//函数返回值:bool类型,返回OK or FALSE
template
bool AVL::Insert(ElemType data)
{
BinTreeNode *posi = Search(data); //记录待插入节点的位置
if (posi != nullptr && posi->data == data)
{ //当要插入的数据已经存在时
return FALSE;
}
BinTreeNode *node;
node = new BinTreeNode;
//将待插入的数据包装成节点
node->data = data;
node->height = 1;
node->leftChild = node->rightChild = nullptr;
node->parent = posi;
if (posi != nullptr)
{ //当树不为空时
(data < posi->data ? posi->leftChild : posi->rightChild) = node;
}
else
{ //当树还为空时
this->root = node;
}
UpdateHeight(*node);
BinTreeNode *g; //g为插入节点的爷节点
g = node->parent;
if (g != nullptr)
{
while (g != nullptr&&abs(CalculateBF(*g)) <= 1)
{ //向上查找失衡节点
g = g->parent;
}
if (g != nullptr)
{ //当存在失衡节点时,进行旋转操作
Rotate(*g); //若爷节点的失衡值的绝对值大于1,进行旋转操作
}
}
return OK;
}
//函数功能:删除节点操作(供用户调用)
//函数参数:待删除的数据
//函数返回值:bool类型,OK or FALSE
template
bool AVL::Delete(ElemType data)
{
BinTreeNode *posi = this->Search(data); //查找待删除的节点
if (posi == nullptr || posi->data != data)
{ //当找不到要删除的节点时,返回FALSE
return FALSE;
}
BinTreeNode *succ; //待删除节点的接替节点,这里用它的前驱结点
BinTreeNode *unbalancedCheckNode; //失衡检查节点
if (posi->leftChild == nullptr)
{ //当删除节点的左孩子为空时
succ = posi->rightChild;
if (posi->parent == nullptr)
{ //当要删除的节点即为根节点时
this->root = succ; //将树的根节点替换成要删除节点的接替节点
if (succ != nullptr) succ->parent = nullptr; //修改接替节点的父节点
}
else
{ //当要删除的节点不为根节点时
(posi->parent->leftChild == posi ? posi->parent->leftChild : posi->parent->rightChild) = succ; //posi的父节点的孩子替换为succ
if (succ != nullptr) succ->parent = posi->parent; //修改接替节点的父节点
}
unbalancedCheckNode = posi->parent; //向上检查失衡
delete posi; //删除节点
posi = nullptr; //将节点置空
}
else if (posi->leftChild->rightChild == nullptr)
{ //当删除节点的左孩子的右孩子为空时
succ = posi->leftChild;
if (posi->parent == nullptr)
{ //当要删除的节点即为根节点时
this->root = succ; //将树的根节点替换成要删除节点的接替节点
succ->parent = nullptr; //修改接替节点的父节点
succ->rightChild = posi->rightChild; //接替节点的右孩子变为删除节点的右孩子
if (posi->rightChild != nullptr) posi->rightChild->parent = succ;
}
else
{ //当要删除的节点不为根节点时
(posi->parent->leftChild == posi ? posi->parent->leftChild : posi->parent->rightChild) = succ; //posi的父节点的孩子替换为succ
succ->parent = posi->parent;
succ->rightChild = posi->rightChild; //接替节点的右孩子变为删除节点的右孩子
if (posi->rightChild != nullptr) posi->rightChild->parent = succ;
}
unbalancedCheckNode = succ; //向上检查失衡
delete posi; //删除节点
posi = nullptr; //将节点置空
}
else
{ //当删除结点的左孩子不为空且左孩子的右孩子不为空
succ = posi->leftChild;
while (succ->rightChild != nullptr)
{ //寻找删除节点的前驱结点
succ = succ->rightChild;
}
posi->data = succ->data; //将删除结点的数据用接替结点的数据代替
unbalancedCheckNode = succ->parent;
succ->parent->rightChild = succ->leftChild; //接替节点的左孩子替代接替节点的父节点的右孩子
if (succ->leftChild != nullptr) succ->leftChild->parent = succ->parent; //更新接替节点左孩子的父节点
delete succ; //删除结点
succ = nullptr; //将指针置空
}
UpdateHeight(*unbalancedCheckNode); //更新树高
BinTreeNode *ancestorNode = unbalancedCheckNode; //删除节点的祖先结点
while (ancestorNode != nullptr)
{ //由于删除操作可能回引起失衡传播,所以要一直向上检查是否失衡
if (abs(CalculateBF(*ancestorNode))>1)
{ //当失衡值的绝对值大于1时进行旋转操作
Rotate(*ancestorNode);
}
ancestorNode = ancestorNode->parent;
}
return OK;
}
//函数功能:将平衡二叉树的节点数据打印出来(供用户调用)
//函数参数:无
//函数返回值:void
template
void AVL::Print()
{
PrintOut(this->root);
}
//函数功能:将平衡二叉树的节点数据打印出来(Private)
//函数参数:开始打印的节点的指针
//函数返回值:void
template
void AVL::PrintOut(BinTreeNode *beginNode)
{ //采用中序遍历
if (beginNode != nullptr)
{
this->PrintOut(beginNode->leftChild);
std::cout << beginNode->data << "\t";
this->PrintOut(beginNode->rightChild);
}
} 以上为平衡二叉树类的模板(继承二叉树类)
我想说的,基本上代码中都注释了。为了程序的安全性考虑,我也尽可能采用引用代替指针以及把一些类函数定义为私有函数,避免被用户滥用。但有同学可能会吐槽这代码怎么会这么长,我只想说,详细注释是有代价的,当然,代码片段中存在部分重复,这是未优化的结果,如果同学们有什么好的改进意见可以在评论区留言给我。上述对二叉树类的定义也过分简单,这是因为这个二叉树类模板我是第一次创建出来的,以后会慢慢会丰富该类模板的接口,不过在这个程序中,这个简单的不能再简单的二叉树类是完全足够的。除此之外,我还是要吐槽这个代码中模板用的形如虚设,因为未对比较操作符(<>=)进行重载,这就导致了比较的范围十分有限,如果再重载比较操作符的话,我们就能比较笔和橡皮的大小了,同学们可以一试。
接下来未测试主函数中的内容:
//平衡二叉树测试函数
//SJ2050
#include
#include "AVL.h"
using namespace std;
int main()
{
AVL *T = new AVL; //创建一棵平衡二叉树
int a[10] = { 3,2,1,4,5,6,7,10,9,8 };
for (int i = 0; i < 10; i++)
{
T->Insert(a[i]);
}
T->Print();
cout << endl; //换行
T->Delete(4);
T->Print();
cout << endl; //换行
T->Delete(2);
T->Print();
cout << endl; //换行
T->Delete(7);
T->Print();
cout << endl; //换行
T->Delete(8);
T->Print();
cout << endl; //换行
T->Insert(11);
T->Print();
cout << endl; //换行
delete T;
system("pause");
return 0;
} 输出结果为:
虽然该程序经过我多次调试,但还是可能存在bug,如果你发现的话,请在评论区告诉我,我会马上修改,谢谢阅读!