二分搜索树的实现以及各种操作(支持重复节点)
二分搜索树
一、 二分搜索树的概念
二分搜索树就是左子树的键值小于根节点,右子树键值大于根节点的树。而且左右子树是递归定义。简单来说就是任意节点左子树的树。这里主要讨论的是二分搜索树也就是二叉树。其应用在于查找表,以及字典结构的时候。其查找速度非常之快,而且可以用其求各种算法例如max ,min ,rank 等等。
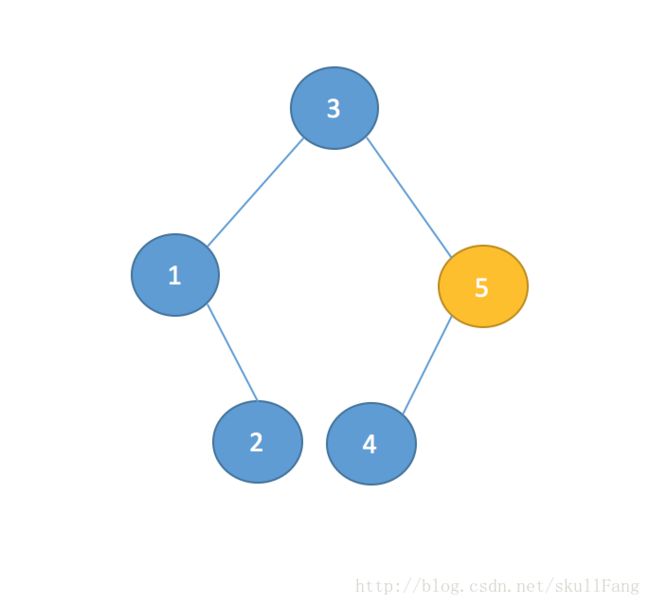
例如这就是一个简单的二分搜搜树
二、为什么要有搜索二叉树
最简单的查找算法就是暴力查找,从待查找序列从头遍历到尾,与查找的key进行对比。
int Search(int *Arr,int n,int key){
for(int i=0;iif(Arr[i]==key)
return i;
}
return -1;
} 这种算法简单暴力,无论查找,插入,删除操作时间复杂度都在O(n),但是这不一定是最好的。在数据量很大的情况此算法显得有点“蠢”,于是人们想到了二分查找(不是二分搜索树)。
也就是每次查找数组的mid
int biSearch(int *Arr,int n,int key){
int l,r;
l=0;r=n-1;
while (l<=r) {
int mid=l+(r-l)/2;// 防止 r,和m足够大越界问题,
if(Arr[mid]==key){// 等于就返回其下标。
return mid;
}
else if(Arr[mid]>key){
r=mid-1; //在左侧进行查找
}
else{
l=mid+1; //在右侧进行查找
}
}
return -1;
} 以上代码是典型的二分查找,在查找方面时间复杂度可以降低到O(logn)级别,但是要求数组一定有序,不是有序的没有办法查找。并且其数据结构为顺序表,也就是说其插入和删除操作时间复杂度还是O(n)级别。那么有没有更优秀的算法使其搜索的时间复杂度为O(logn),插入和删除操作也为O(logn)呢,答案是肯定的,也就是今天的主角。二分搜索树。
三、二分搜索树
3.1 二分搜索树的定义
为了充分体现二分搜索树的优势和使用技巧,这里所做的二分搜索树是一个字典样式的树,也就是说其有key值,和value值。并且其用的是树的链表法去存储,所以也有节点这个概念。节点定义特别很简单,跟普通的树是一样的。
struct Node{
int value;
int key;
int frequency; // 本次做的二分搜索树是支持重复节点的,这个是记录该节点的重复次数
Node *left;
Node *right;
Node(int key ,int value){
this->value=value;
this->key=key;
this->left=this->right=NULL;
this->frequency=1;
}//构造函数
};为了方便操作在这里构建的一个BST的类。
class BST{
private:
struct Node{
int value;
int key;
int frequency;
Node *left;
Node *right;
Node(int key ,int value){
this->value=value;
this->key=key;
this->left=this->right=NULL;
this->frequency=1;
}//节点构造函数
};
Node *root; //root为根
int count; // count记录的shi当前树中拥有节点的个数
public:
BST(){
root=NULL;
count=0;
} //BST树的构造函数
};各位看客朋友请好好看看上面类的结构,接下来的所有操作都是基于上述类的。
3.2 二分搜索树的建立
其实树的建立就是一个插入过程,每次插入都不改变其树的性质和结构。
这里利用的树的天然递归性质进行插入的操作。
Node *insert(Node *node,int key,int value){
if(node==NULL){
count++;
return new Node(key,value); //如果没有这个节点就用结构体的构造方法,new一个节点。
}
if(node->key< key){
node->right=insert(node->right,key,value); //右边去看看
}
else if(node->key>key){
node->left=insert(node->left,key,value); //左边去看看
}
else if(node->key==key) // 因为允许重复key值的插入,所以有重复key值的时候要更新节点信息
{
node->value=value; //可以不要
node->frequency++; // 该节点的频度要++
}
return node; //返回的就是这个数的根
}在类的public中定义一个insert 函数,让这个二分搜索树的根传入进去即可。
void insert(int key,int value){
root=insert(root,key,value);
}大功告成,这样就能做出来一个二分搜索树。
3.3 二分搜索树的搜索操作
跟顺序表的二分搜索一样。废话不多说。直接贴代码
int search(Node *node,int key){
if(node!=NULL )
{
if(node->key==key){
return node->value;
}
else if(node->key>key){
return search(node->left,key);
}
else
{
return search(node->right,key);
}
}
return -1;
}对应着在public 中定义一个search方法
int search(int key){
return search(root,key);
}是不是优雅高效?复制即可用。
3.3 二分搜索树的删除
这一步就麻烦了。
分几种情况。
a. 没有左孩子
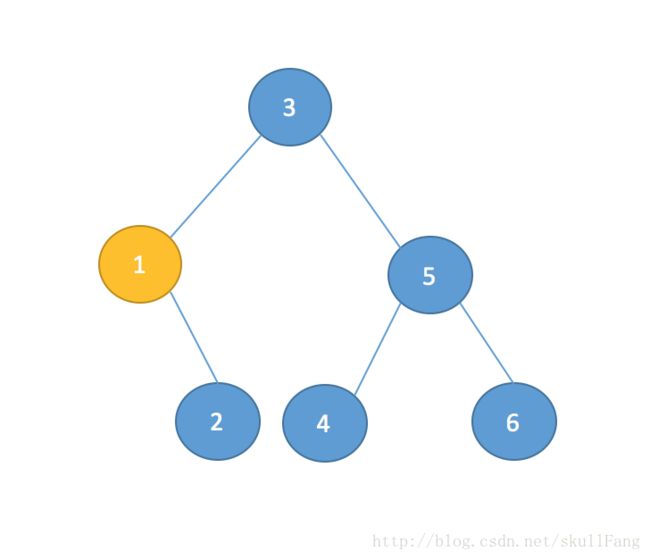
遇到这种情况怎么办呢
其实很简单只需要用 这个节点的右孩子代替其位置即可。
于是有了
if(node->left==NULL){
Node *rightNode=node->right; //拿到右孩子
delete node; //大胆删除节点
count--; // 数量--
return rightNode; //将其返回
} if(node->right==NULL){
Node *leftNode=node->left; //拿到左孩子
delete node;
count--;
return leftNode;
}c. 有左孩子也有右孩子

这个时候怎么办呢,其实只要找到右子树上最小的那个节点代替即可。
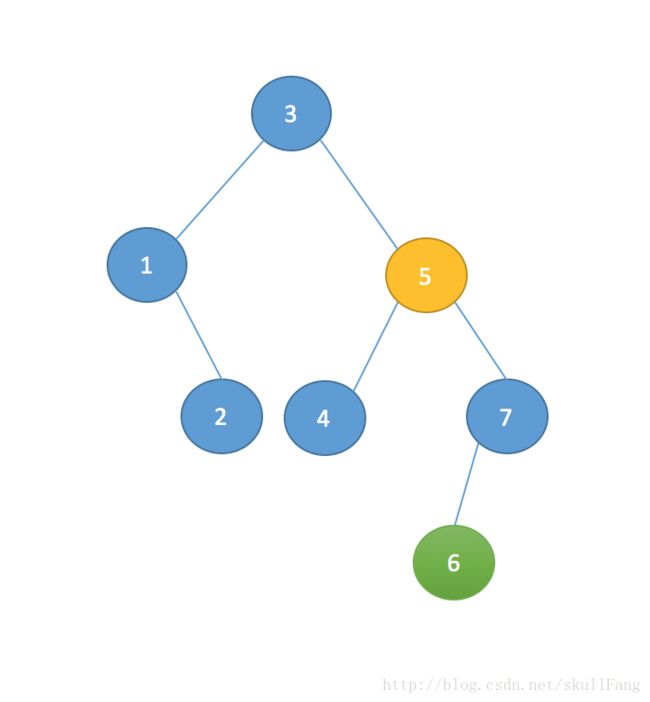
那么怎么去找这个最小的节点呢?很容易发现其实这个节点就是右子树最左边的那个节点。那么这个节点有什么特性呢?很明显这个节点是没有左孩子。
Node* minimun(Node *node){
if(node->left==NULL){
return node; // 成功找到这个节点
}
return minimun(node->left);
}找到这个节点后就要想办法把它拿上来,并且被删除那个节点的左孩子和右孩子都要给他。
Node *s=new Node(minimun(node->right)); //用s复制该节点的右子树的最小值的那个节点
count++;
s->right=removeMin(node->right);//把右子树那个最小值删掉并且做s的右子树
s->left=node->left;
delete node;
count--;
return s;细心的同学会发现 这里使用了Node(Node *node)这样的构造函数,这是在类中没有的,所以我们要在类中定义一个重载的节点构造函数。(仅仅是复制而已!)
Node(Node *node){
this->value=node->value;
this->key=node->key;
this->right=node->right;
this->left=node->left;
this->frequency=node->frequency;
}好了不要晕,这里贴出完整代码
Node *remove(Node *node,int key){
if(node==NULL){
return NULL;
}
if(node->key==key){ //找到这个节点
if(node->left==NULL){// 情况a
Node *rightNode=node->right;
delete node;
count--;
return rightNode;
}
if(node->right==NULL){ //情况b
Node *leftNode=node->left;
delete node;
count--;
return leftNode;
}
// node->left!=NULL && node->right!=NULL 情况c
Node *s=new Node(minimun(node->right)); //用s复制该节点的右子树的最小值的那个节点
count++;
s->right=removeMin(node->right);//把右子树那个最小值删掉并且做s的右子树
s->left=node->left;
delete node;
count--;
return s;
}
else if(node->key>key){ //左边找找看
node->left=remove(node->left,key);
return node;
}
else{ //右边找找看
node->right=remove(node->right,key);
return node;
}
}相应在类中加入这个remove函数
void remove(int key){
root=remove(root,key);
} // 简单粗暴这里基本操作讲完了,也就是插入,查找,删除。其时间复杂度都为O(logn)。
四、其他操作
这里贴出整个类的代码以及测试例子,供大家观赏。
#include <iostream>
#include <queue>
#include <ctime>
using namespace std;
//template 上面所有操作都封装很好,可供大家二次开发,如果各位觉得有用复制之后点个赞哦!!!