GLSL核心课程---纹理坐标
纹理坐标通常用作如何将一个一张图片贴到表面上。然而纹理坐标并不是限制执行这种贴图。纹理坐标本身同样也可以用作绘画模型。在这里我们用两个例子来说明纹理坐标如何使用。
第一步就是使纹理坐标在我们的着色器有效。纹理坐标仅仅是又一个属性变量,就像法向量一样。因此在应用程序中,我们需要像这样处理,比如,我们需要添加包含纹理坐标的包含其他属性的顶点数组对象的缓冲区(请看这一节来了解更多属性细节)。
在顶点着色器中我们需要接收纹理坐标作为输入,通常的做法就是将它直接作为输出变量,这个变量同样也会在片段着色器中作为输入,我们可以用它来产生应用程序所需要的结果。
下面的代码描述上面的处理:
顶点着色器
#version 330
in vec4 position;
in vec2 texCoord;
out vec2 texCoordV;
uniform mat4 m_pvm;
void main()
{
texCoordV = texCoord;
gl_Position = m_pvm * vec4(position, 1.0);
}
片段着色器:
#version 330
in vec2 texCoordV;
out vec4 FragColor;
void main()
{
FragColor = vec4(texCoordV, 0.0, 0.0);
}
这些着色器的输出是将纹理坐标作为颜色值使用,展示了如何将纹理贴到模型中。实际上,下面的图展示了一个平面、一个大象、和一个茶壶,和它们的纹理坐标。红色将用s坐标,和绿色将用t坐标。这些着色器可以调试在一个图像纹理贴图中产生意外的效果。
玩转纹理坐标
纹理坐标同样可以使用产生有趣的效果。例如,假设我们想产生以下这幅图的网格效果:
为了得到上面的效果,我们只能绘制某些像素(用蓝色)然后使用GLSL关键字discard来丢弃其他像素。网格的密度由纹理坐标乘以缩放来定义。在片段着色器中选择那些纹理坐标小数部分值小于0.1的像素,然后用蓝色来绘制。这个最后值,0.1用来控制绘制线的宽度。
顶点着色器跟之前一样,仅仅片段着色器需要重写。下面我们设置了缩放系数为8。通过这个值和门槛值来分别改变网格单元的数目和它们的宽度。
#version 330
in vec2 texCoordV;
out vec4 FragColor;
uniform int multiplicationFactor = 8;
uniform float threshold = 0.1;
void main()
{
vec2 t = texCoordV * multiplicationFactor;
if(fract(t.s) < threshold || fract(t.t) < threshold)
FragColor = vec4(0.0, 0.0, 1.0, 1.0);
else
discard;
}
关键字discard导致片段着色器丢弃(像素)。这个将导致着色器停止然后不向缓冲区写任何的数据,包括颜色和深度。
另外一个有趣的例子就是基于纹理坐标的颜色拾取。例如,我们可以写一个着色器来绘制一个带有条纹的物体。这个着色器将决定如何基于纹理坐标的小数值来决定颜色值。实际上如果纹理坐标的小数值小于0.5,着色器将会拾取一个意思,否则其他意思将会被拾取。
当然,仅仅片段着色器需要重写:
#version 330
uniform vec4 color1 = vec4(0.0, 0.0, 1.0, 1.0);
uniform vec4 color2 = vec4(1.0, 1.0, 0.5, 1.0);
uniform int multiplicationFactor = 8;
in vec2 texCoordV;
out vec4 FragColor;
void main()
{
if(fract(texCoordV.s * multiplicationFactor) < 0.5)
FragColor = color1;
else
FragColor = color2;
}
这个例子有明显的锯齿。这是因为我们在颜色函数中使用一个阶梯函数。为了混合这个我们可以使用一个光滑转换函数,就像下面展示的:
在片段着色器中为了实现这个效果还是相当简单的。我们将像下面看到的使用GLSL混合函数来线性插值颜色值。第一步混合函数的两个参数就是要混合的颜色,最后一个参数将控制如何混合,通过下面的方程式:
![]()
片段着色器可以这么写:
#version 330
Uniform vec4 color1 = vec4(0.0, 0.0, 1.0, 1.0);
Uniform vec4 color2 = vec4(1.0, 1.0, 0.5, 1.0);
Uniform int multiplicationFactor = 8;
In vec2 texCoordV;
Out vec4 FragColor;
Void main()
{
Vec2 t = texCoordV * multiplicationFactor ;
Float f = fract(t.s);
If(f < 0.4)
FragColor = color1;
Else if(f < 0.5)
FragColor = mix(color1, color2, (f - 0.4) * 10.0);
Else if(f < 0.9)
FragColor = color2;
Else
FragColor = mix(color2, color1, (f - 0.9) * 10.0);
}
观察下面的截图,后面的例子(右边)相比较于左边明显有改进:
GLSL有一个也可以产生同样效果的函数:smoothstep。这个函数有三个参数:一个下界限(edge0),一个上界限(edge1)和一个源插值。
代码片段:
if(x <= edge0)
return 0.0;
else if x > edge1
return 1.0;
else
{
t = (x - edge0) / (edge1 - edge0);
return 3.0 * t ^ 3 - 2.0 * t ^ 2;
}
在edge0和edge1之间,这个函数会在0到1之间执行埃尔米特插值(平滑三次曲线)。
这里有两个例子展示了不同参数的曲线值:
f = smoothstep(0.4, 0.5, x);
f = smoothstep(0.9, 1.0, x);
上面没有我们要找的,但是当我们结合这两个的时候,就可以得到我们想要的。
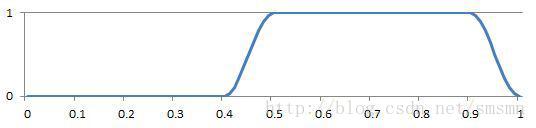
f = smoothstep(0.9, 1.0, t.s) - smoothstep(0.4, 0.5, t.s);
结果的f值还可以用在混合函数的参数中来决定最后的颜色。片段着色器可以像这样写:
#version 330
uniform vec4 color1 = vec4(0.0, 0.0, 1.0, 1.0);
uniform vec4 color2 = vec4(1.0, 1.0, 0.5, 1.0);
uniform int multiplicationFactor = 8;
in vec2 texCoordV;
out vec4 FragColor;
void main()
{
float x = fract(texCoordV.s * multiplicationFactor);
float f = smoothstep(0.4, 0.5, x) - smoothstep(0.9, 1.0);
FragColor = mix(color1, color2, f);
}
英文地址