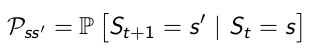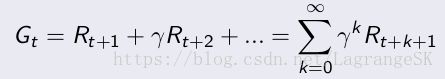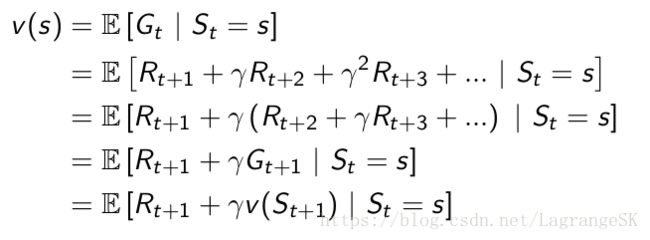强化学习二:Markov Processes
一、前言
在第一章强化学习简介中,我们提到强化学习过程可以看做一系列的state、reward、action的组合。本章我们将要介绍马尔科夫决策过程(Markov Decision Processes)用于后续的强化学习研究中。
二、马尔科夫过程(Markov Processes)
2.1 马尔科夫性
首先,我们需要了解什么是马尔科夫性:
当我们处于状态StSt时,下一时刻的状态St+1St+1可以由当前状态决定,而不需要考虑历史状态。
未来独立于过去,仅仅于现在有关
将从状态s 转移到状态 s’ 的转移概率简写为Pss′:
那么所有状态间的转移关系可以由状态转移矩阵表示:
2.2 马尔科夫过程
马尔科夫过程也称为马尔科夫链,由一些具有马尔科夫性的量随机组成的记忆链,这些量之间有转移概率。如具有马尔科夫性的state可以组成马尔科夫链 S1,S2,...其定义如下:
2.3 小例子:student Markov Chain
以学生上课为例子,假设一学期只有三节课,那么在class 1的状态下有0.5的概率前往class 2,另外0.5的概率会去看Facebook。看Facebook会停不下来,所以有0.1的概率回到class1,而有0.9的概率继续看。假如我们从 class1到了class2,上课觉得无聊有0.2的几率会睡觉,另外0.8的概率咬牙坚持到class3。到了class 3 后,想到上课快上完了,去泡个吧(0.4 go to pub),然后喝断片了,忘了上课内容,会随机回到class1、class2、class3。从class 3有0.6的概率会通过考试,考试完了就肯定回去睡觉啦,在这里sleep是一个最终状态。
三、 马尔科夫决策过程
介绍了马尔科夫链后,自然有个疑问什么是马尔科夫决策过程(MDP)?
首先,我们介绍Markov Reward Process(MRP),再从MRP演变到MDP。
3.1 Markov Reward Process
最开始说到马尔科夫链是由一些具有马尔科夫性的量随机组成的记忆链,那么MRP就是关于价值的马尔科夫链。 
和上面的关于state的马尔科夫链相比,增加了reward RR 和discount γγ(红色标出),我们已经知道reward的定义,那么为什么会有discount γ(折扣因子)呢?
3.1.1 Return
在强化学习中,我们关注的不仅仅是当前的reward,因为状态的转移可能对未来的收益都有影响,所以我们关注的是总体reward之和:
这个式子好像不是单纯的reward之和啊!果然,这是一个有心机的reward之和,他包含了我们好奇的 discountγγ。为什么要有这个呢?
为了数学上使得reward之和收敛,此处选择了一个折扣因子 0=<γ<=1 .
可能我们的模型(转移概率)不够完备,选择γγ 可以减小未来reward对return的影响
另外,当γ=1时,表明未来以及现在的reward具有相同的权重,可以说此时的agent是一个 far-sighted
当γ=0时,表明完全不考虑未来的reward,只考虑当下,可以说此时的agent是一个 myopic
3.1.2 value Function
通常return依赖于状态之间的转移顺序,那么我们如何描述某一个特定状态 s 下能够获得的reward之和呢,还是看一下之前的小例子,此处我们加上了单步reward。
假如我们此时处在class1 的状态,那么我们可能有如下几个状态链
假设此处的discountγ=1/2,根据公式计算他们的return 分别如下
那么我们自然想到,可以通过求这些return的平均来计算出class1的价值。
这也是价值函数的定义:
其中,E表示期望。
将value function 带入到Student MRP中可以得到State-Value Function for Student MRP:
可以看到用value function取代了state。
Bellman公式在强化学习中常用Backup图表示,如下:
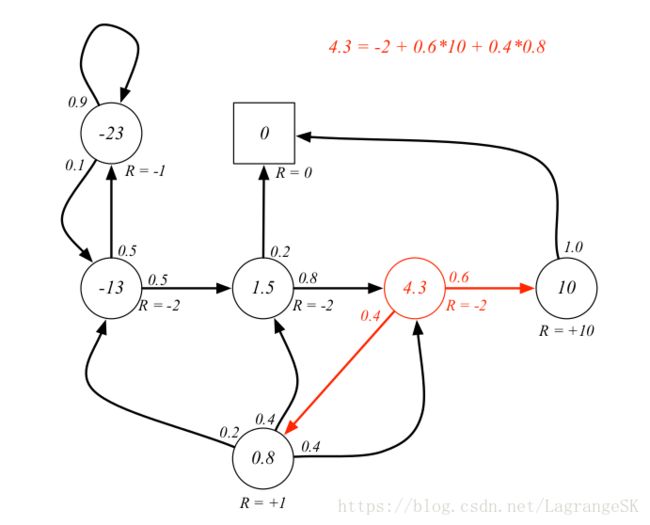
当我们从当前状态 s 转移到下一时刻状态时,对下一时刻每一个状态s’ 存在一个从状态s 到 s’的状态转移概率 Pss′,那么当前状态的value function 可以表示为当前状态的reward 加上,带discount的下一时刻状态s与状态转移概率 Pss′乘积的累加和。
观察红色位置,也就是s=class3s=class3时,当前状态的value functionv(s)=4.3 ,reward Rs=−2,下一时刻状态有两个Rs=−2,下一时刻状态有两个s’_1 = Pass(概率0.6)和(概率0.6)和s’_2=Pub(概率0.4),(概率0.4),v(s’_1 )=10 v(s’_2)=0.8$,计算公式见图右上角。
当然,Bellman 等式可以用矩阵形式表示为:
v=R+γPv
那么很自然我们就会想到能不能通过矩阵求解的形式来求解,
但是我们不能,原因如下:
这个问题的计算复杂度为O(n3)O(n3),我们只能对维度较小 的MRP直接求解
另外有很多迭代的方式可以求解:
Dynamic programming(动态规划)
Monte-Carlo evaluation(蒙特卡洛)
Temporal-Difference learning(时间查分)
3.2 Markov Decision Process(MDPs)
说完了MRPs,那么他和MDPs有什么关系呢,简单来说,多了一个采取动作的过程,这个动作就是决策(decision),定义如下: 
student MDP如下:
和student MRP 比较,增加了动作量。
3.2.1 Policy
增加了动作后,我们需要考虑当前状态下选择动作的概率,也就是策略。策略表示在状态s下采取动作a的概率:
3.2.2 value function
value function可以分为状态价值函数v(s)和动作价值函数q(s,a):
q(s,a)q(s,a)满足Bellman等式:
3.2.3 Bellman Expectation Equation
附上几张Backup图,便于理解BellmanBellman Expectation Equation:
-
从state到action:
从action到state:
-
-
采取一个动作,首先会获得一个reward,然后从状态s转移到状态s’,结合MRP中第一个 backup图,可得。
-
从state 到state
结合上面两个backup图,从一个state经过一个action到另一个state价值函数间的关系可以表示为:
-
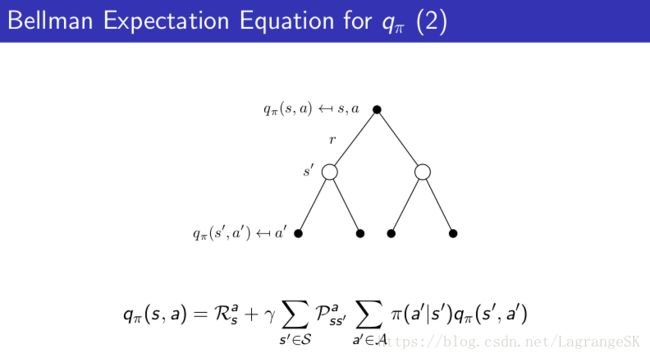
从action到action
结合上面两个backup图同时可以获得,从一个action到另一个action的价值函数关系:
则对应的例子图为
观察红色部分,当s=Passs时, 有两个action可供选择,分别为study和pub,假设两者概率相等,即π(s,a1)=π(s,a2)=0.5由Backup图(state到state)得右上角红色等式。
3.2.4 最优价值函数
讲到这里,你可能已经开始想,我关心的是我怎么做才能取得最好的结果,而不是这些状态函数的自身的迭代关系。那么,你需要找到最优值函数。
3.2.5 最优策略
当我们找到最优值函数是否意味着我们找到了最优策略呢?答案是肯定的。当一个策略比其他策略好,那么其值函数大于别的策略的值函数。
可以依据这一定理选择最优策略:
如图:
3.2.6 Bellman 最优公式
列出几个BackUP图方便理解Bellman最优公式:
![]()
和普通Bellman公式不同的是,Bellman最优公式表示的是最优值函数之间的关系,当我们处于state s的时候,下一步要选择一个action,但是现在有很多action,每个action a 在状态 s 下都有对应着一个最优动作值函数 q∗(s,a)。那么显然选择最大的那个 q∗(s,a)就是当前的最优状态值函数。
从action到state
当我们选择了一个动作后,自然产生一个reward,然后我们会有一定几率转移到状态s’,注意,这里没有一个最大化的过程。
从state到state:
结合上面两个Backup图可得
从action到action:
结合上面两个Backup 图可得
那么有了Bellman等式,我们基于student MDP 例子来了解一下具体计算过程吧!