计算机视觉CV中特征点提取SURF算法的学习笔记

1 致谢

感谢网友tongle.Wang的帮助，

链接如下：

https://blog.csdn.net/ecnu18918079120/article/details/78195792

2 SURF算法介绍

SURF 算法，全称是 Speeded Up Robust Features。该算子在保持 SIFT 算子优良性能特点的基础上，同时解决了 SIFT 计算复杂度高、耗时长的缺点，对兴趣点提取及其特征向量描述方面进行了改进，且计算速度得到提高。

3 SURF算法主要步骤

3.1 构造特征点

3.1.1 构造Hessian矩阵，并计算其特征值

SURF构造的金字塔图像与SIFT有很大不同，就是因为这些不同才加快了其检测的速度。SIFT采用的是DOG图像，而SURF采用的是Hessian矩阵行列式近似值图像。

接下来，我们来介绍一下Hessian矩阵，

黑塞矩阵（Hessian Matrix）是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。由德国数学家Ludwin Otto Hessian于19世纪提出。
SURF算法构造的金字塔图像与SIFT有很大不同，SIFT采用的是DoG图像，而SURF采用的是Hessian矩阵行列式近似值图像。所以说，Hessian矩阵是Surf算法的核心，构建Hessian矩阵的目的是为了生成图像稳定的边缘点（突变点），为下文的特征提取做好基础。

Hessian矩阵的定义如下，

 

3.1.2 构造尺度空间

构造尺度空间是为了在空间域与尺度域上找到极值点，作为初步的特征点。构造尺度空间传统的方法即构造一个高斯金字塔，原始图像作为最底层，然后对图像进行高斯模糊再降采样（2倍）作为下一层图像，循环迭代下去。高斯金字塔是对原图像的尺寸是在不断变化的，高斯模板尺寸不变。每一层的建立必须等到上一层构造完毕后才能进行处理，依赖性很强，这样造成速度上很慢。

SURF构建尺度金字塔的方法采用原图像大小不变，变化的是模板大小，即采用变化的模板盒子尺寸对原图像进行滤波，构造出尺度空间。（这同时说明，不同尺寸的高斯滤波模板可以用来模拟不同尺度的图像效果）；同时，SURF可以采用并行运算，对金字塔中的每层图像同时进行处理。通过逐渐增大的盒子尺寸滤波模板与积分图像卷积产生的Hessian矩阵行列式的响应图像，构造出金字塔。

3.1.3 对Hessian矩阵进行极值点检测

在文章中，提到了NMS算法其实，就是具体来说就是SIFT算法中的“极值点检测”。NMS方法也是使用极值来初步定位特征点，如下图，将Hessian矩阵处中的每个像素点与其3维领域的26个点进行大小比较，取其中的最大值或者最小值作为极值，最后获得极值点图像数据。

3.1.4 准确定位特征点

（文章中提到了3D非极大值抑制，根据陈助教的解释，其实就是上面的极值点检测）由于极值点图像是离散空间的数据，通过拟合方法，准确定位到特征点的位置，每个特征点包含三个信息H(x,y,σ)，即位置与尺度。这个步骤与SIFT的方法相似。

 

3.2 构造特征点描述子

3.2.1 选取特征点主方向

（这一步根据名称来说，好像也是在确定特征点的信息，但是其实这里对于过程的划分也没有过于准确的要求，这里我们的划分方法，是根据论文中的描述顺序来进行的，所以为了保持跟论文的叙述顺序一致，我们把“选取特征点主方向”的步骤也放到“构造特征描述子”中来）  

为了保证旋转不变性，在SURF中，没有统计特征点的梯度直方图，而是统计了特征点邻域内的Harr小波特征。即以特征点为中心，计算半径为6s(s为特征点所在的尺度值)的邻域内，统计60度扇形内所有点在X(水平)和Y(垂直)方向的Haar小波响应总和(Haar小波边长取4s)，并给这些响应值赋高斯权重系数，使得靠近特征点的响应贡献大，而远离特征点的响应贡献小，然后60度范围内的响应相加以形成新的矢量，遍历整个圆形区域，选择最长矢量的方向为该特征点的主方向。这样，通过特征点逐个进行计算，得到每一个特征点的主方向。该过程的示意图如下：

相邻的60°扇形区域之间可能会存在重叠（overlap），关于具体的重叠比例还要查看论文的源代码。

3.2.2 构成描述子

在这里，将使用已有的特征点信息来构造特征描述子。
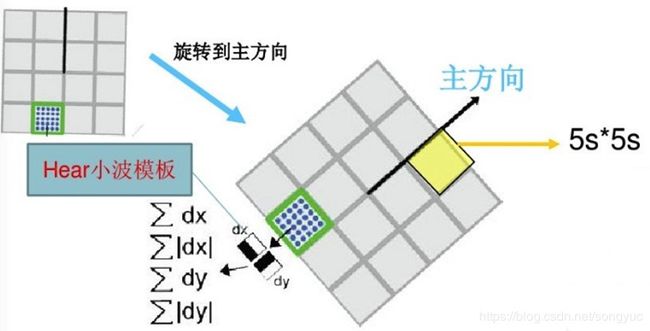
对于每个特征点，沿着其主方向，取特征点周围20s×20s的矩形区域作为其邻域，其中s为特征点的尺度值；然后将矩形窗分成4×4个子区域，统计每个子区域内像素点的Harr小波响应，沿着主方向与垂直于主方向的响应，Harr小波滤波器宽度为2s。统计16个子区域的响应信息，每个子区域采用下面公式的方法进行统计，同时每个像素点的响应要乘以对应位置的高斯权重（σ = 3.3s）。其计算过程如下图所示，

这样每个子区域携带4个信息，即，共有16个子区域，共64维。其中，小波响应的使用会使该方法具有光照无关的效果。

尺度无关性是通过将描述子向量转换为单位向量来实现的。

3.3 特征点匹配

与SIFT特征点匹配类似，SURF也是通过计算两个特征点间的欧式距离来确定匹配度，欧氏距离越短，代表两个特征点的匹配度越高。
不同的是SURF算法还加入了Hessian矩阵迹的判断，如果两个特征点的矩阵迹正负号相同，代表这两个特征具有相同类型的对比度变化，如果不同，说明这两个特征点的对比度变化方向是相反的，即使欧氏距离为0，也直接予以排除。