第二类曲面积分某问题

问题

看到这样的问题

∬S+x2dy∧dz+y2dx∧dz+z2dx∧dy

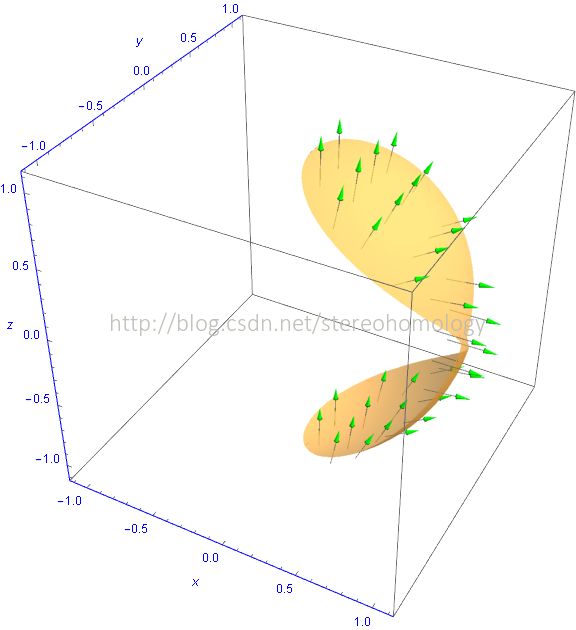
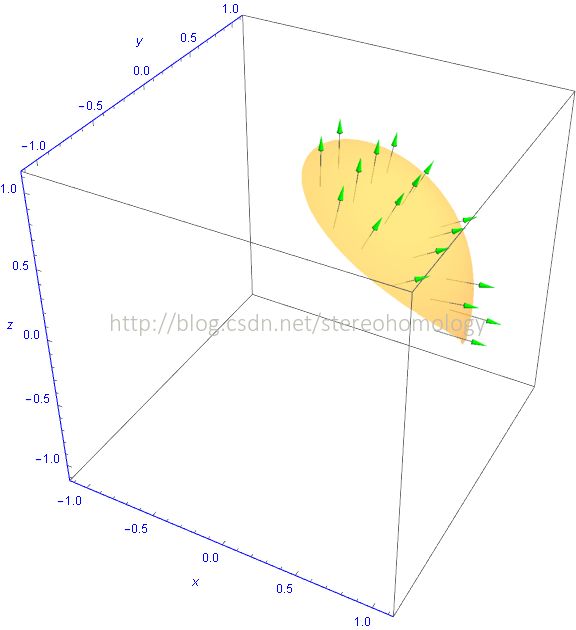
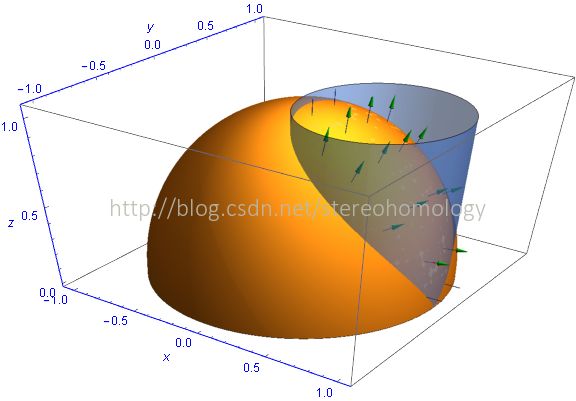
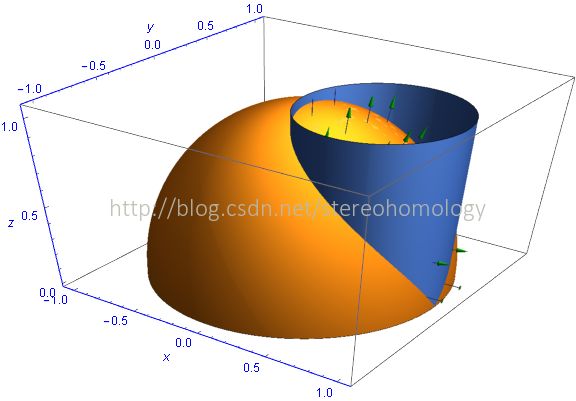
其中 S+ 是 球面 x2+y2+z2=1 上半球的、夹在圆柱面 x2−x+y2=0 之内的 部分的 外面。

我自己第二类曲面积分学得不好，考试也是靠死记公式和习题通过的，并没有理解，以至于还有些看似简单的问题自己搞不定；现在回过头来温习一下这道习题，查查资料、问问高手们，动手算算，写出来对比对比，发现很有收获，对教科书上的概念和公式的理解又深入了一些。

分析

被积的向量场 (x2,y2,z2) 很简单, 关键是有向曲面：

取的是下面图片中的上半片：

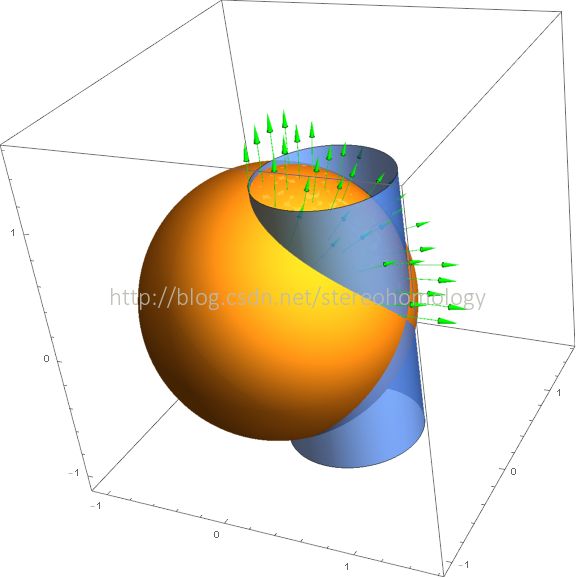
看图片似乎出自某中文图书中的“习题”。如果不出图，纯想象，看上去还是有难度的。然而，作业题意味着，积分的计算应该不会太难。

第二类曲面积分的求解，除了能够利用定理的之外，通常是转化为二重积分之后再计算的。

国内多元微积分教材上的方法是下面公式中左侧逐项计算的方法，对被积的有向曲面向三个不同坐标平面作投影（这个曲面特殊时难度很高）。这种方法，英文多元微积分教材上不太容易找到。英文教材里面通常推荐的是使用下面公式的右边计算：

∬S+Fxdydz+Fydxdz+Fzdxdy=∬SF⃗ ⋅n⃗ dS

左边是有向曲面，右边是方向去掉了之后的二重积分。国外教材的方法似乎更容易用程序实现。还是我理解的不够透彻？

被积曲面三个投影上的二重积分

从编程序的角度，这种方法繁琐。这个向量场三个分量都有的情形，要对有向曲面向三个坐标平面都作投影、分别计算曲面上的二重积分。

其中，投向 xoy 的部分最简单，是一个圆（用参数形式或极坐标表示之后、再二重积分）；而投向 yoz 的投影，是一个简单双纽线上半部包围的区域。

但是，投向 xoz 的部分，实际上会有重叠，似乎要分上下两个面分别计算，它们刚好镜像对称而且边界主要是抛物线和圆弧这样的二次曲线段拼接起来的封闭区域（因为刚好有向曲面镜像对称，从而上下两片的二重积分可以抵消）；

∬σyz(1−y2−z2)dσyz+0+∬σxy(1−x2−y2)dσxy

两个二重积分：

=∫1z=0∫z2−z4√y=−z2−z4√(1−y2−z2)dz+∫1x=0∫x−x2√y=−x−x2√(1−x2−y2)dydx

结果是，在参考答案部分。

向量场和曲面法向量内积的二重积分

有向曲面块的参数化描述，首先它是 x2+y2+z2=1 上半球面的一部分，所以，用两个参数能够表示成 (x,y,1−x2−y2−−−−−−−−−√) ，其次，圆柱的底也就是被积部分在 xoy 上的投影 x2−x+y2=0 ，所以，是 x2−x+y2<=0 的区域， y∈[−x−x2−−−−−√,x−x2−−−−−√],x∈[0,1] 。

∬SF⃗ ⋅n⃗ dS

是一个关于 标量函数 F⃗ ⋅n⃗ =(x2,y2,z2)⋅(x,y,z)=x3+y3+z3 的二重积分，积分的变量是此时表示 无向曲面 S 的 x,y 两个变量：

∬SF⃗ ⋅n⃗ dS=∬S(x3+y3+z3)dS

=∬Dxy(x3+y3+z3)A2+B2+C2−−−−−−−−−−−√dydx

( A,B,C 是曲面参数方程 (x,y,z=1−x2−y2−−−−−−−−−√) 中关于曲面参数 (x,y) 的三个雅克比行列式： A=D(y,z)D(x,y)=x1−x2−y2−−−−−−−−−√ , B=D(z,x)D(x,y)=y1−x2−y2−−−−−−−−−√ , C=D(x,y)D(x,y)=1 )

=∫1x=0∫x−x2√y=−x−x2√x3+y3+(1−x2−y2)3/21−x2−y2−−−−−−−−−√dydx

完全成为一个二重积分问题。用极坐标会方便些吗？但是答案已经可以出来了。

程序计算

变成二重积分之后，都容易用程序计算了。新版10+Mathematica对隐函数形式描述的不规则区间积分的功能，让问题也变得很容易。更像是直接使用 F⃗ ⋅n⃗  ，深入的技巧不能用前述表达，贴代码

Integrate[#,{x,y,z}∈ImplicitRegion[x^2+y^2+z^2==1 && x^2 -x +y^2<= 0 && z>= 0,
 {x,y,z}]]&@ ({x^2, y^2, z^2} . {x, y, z})

参考答案

不论如何，这道题对之前的我来说都是难求的。如果考试这道题，闭卷，我可能要吃鸭蛋。写出来，主要是把这个鸭蛋吃掉。

38105+5π32