import bisect
from bisect import bisect_right
import matplotlib.pyplot as plt
import numpy as np
import math
lr = []
iters=[]
def _get_warmup_factor_at_iter(
method: str, iter: int, warmup_iters: int, warmup_factor: float
):
"""
Return the learning rate warmup factor at a specific iteration.
See :paper:`in1k1h` for more details.
Args:
method (str): warmup method; either "constant" or "linear".
iter (int): iteration at which to calculate the warmup factor.
warmup_iters (int): the number of warmup iterations.
warmup_factor (float): the base warmup factor (the meaning changes according
to the method used).
Returns:
float: the effective warmup factor at the given iteration.
"""
if iter >= warmup_iters:
return 1.0
if method == "constant":
return warmup_factor
elif method == "linear":
alpha = iter / warmup_iters
return warmup_factor * (1 - alpha) + alpha
else:
raise ValueError("Unknown warmup method: {}".format(method))
class WarmupMultiStepLR():
def __init__(
self,
milestones,
gamma: float = 0.1,
warmup_factor: float = 0.001,
warmup_iters: int = 50,
warmup_method: str = "linear",
):
if not list(milestones) == sorted(milestones):
raise ValueError(
"Milestones should be a list of" " increasing integers. Got {}", milestones
)
self.milestones = milestones
self.gamma = gamma
self.warmup_factor = warmup_factor
self.warmup_iters = warmup_iters
self.warmup_method = warmup_method
def get_lr(self, iter) :
warmup_factor = _get_warmup_factor_at_iter(
self.warmup_method, iter, self.warmup_iters, self.warmup_factor
)
return [
base_lr * warmup_factor * self.gamma ** bisect_right(self.milestones, iter)
for base_lr in [0.001]
]
class WarmupCosineLR():
def __init__(
self,
max_iters: int,
warmup_factor: float = 0.001,
warmup_iters: int = 50,
warmup_method: str = "linear",
):
self.max_iters = max_iters
self.warmup_factor = warmup_factor
self.warmup_iters = warmup_iters
self.warmup_method = warmup_method
def get_lr(self, iter):
warmup_factor = _get_warmup_factor_at_iter(
self.warmup_method, iter, self.warmup_iters, self.warmup_factor
)
# Different definitions of half-cosine with warmup are possible. For
# simplicity we multiply the standard half-cosine schedule by the warmup
# factor. An alternative is to start the period of the cosine at warmup_iters
# instead of at 0. In the case that warmup_iters << max_iters the two are
# very close to each other.
return [
base_lr
* warmup_factor
* 0.5
* (1.0 + math.cos(math.pi * iter / self.max_iters))
for base_lr in [0.01]]
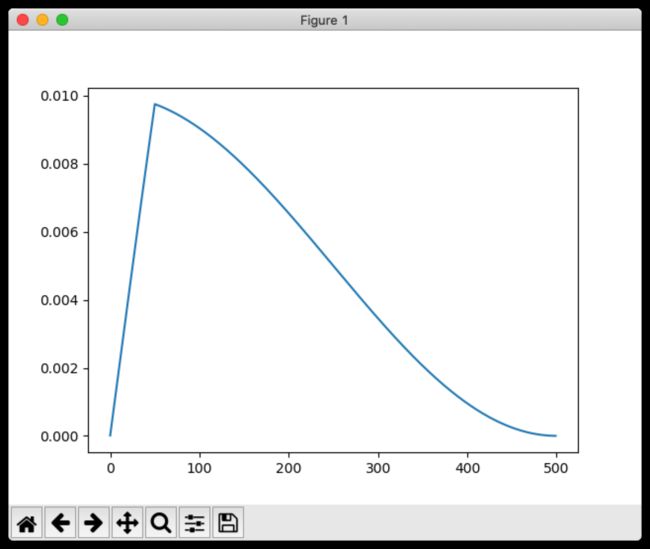
coslr = WarmupCosineLR(max_iters = 500)
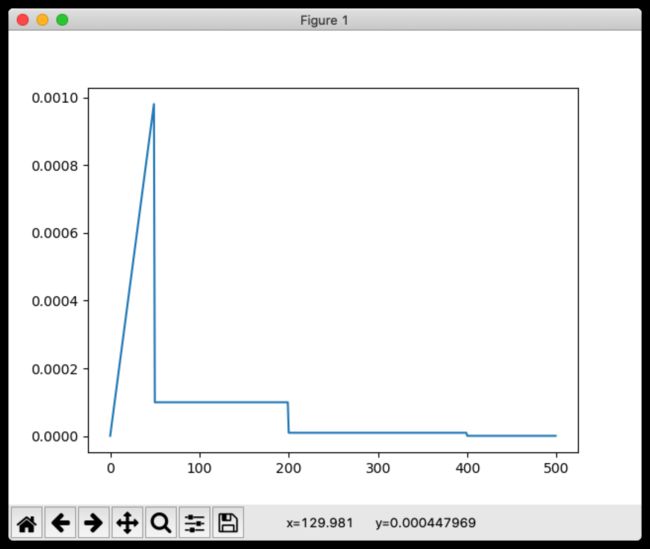
linlr = WarmupMultiStepLR(milestones=[50,200,400])
for iter in range(500):
lr.append(linlr.get_lr(iter))
iters.append(iter)
plt.plot(iters,lr)
plt.show()