7-2 哈利波特的考试（最短路径 - Floyd算法）

哈利·波特要考试了，他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha，将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念，例如ahah可以将老鼠变成猫。另外，如果想把猫变成鱼，可以通过念一个直接魔咒lalala，也可以将猫变老鼠、老鼠变鱼的魔咒连起来念：hahahehe。

现在哈利·波特的手里有一本教材，里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场，要考察他把这只动物变成任意一只指定动物的本事。于是他来问你：带什么动物去可以让最难变的那种动物（即该动物变为哈利·波特自己带去的动物所需要的魔咒最长）需要的魔咒最短？例如：如果只有猫、鼠、鱼，则显然哈利·波特应该带鼠去，因为鼠变成另外两种动物都只需要念4个字符；而如果带猫去，则至少需要念6个字符才能把猫变成鱼；同理，带鱼去也不是最好的选择。

输入格式:
输入说明：输入第1行给出两个正整数N (≤100)和M，其中N是考试涉及的动物总数，M是用于直接变形的魔咒条数。为简单起见，我们将动物按1~N编号。随后M行，每行给出了3个正整数，分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100)，数字之间用空格分隔。

输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度，中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的，则输出0。如果有若干只动物都可以备选，则输出编号最小的那只。

输入样例:

6 11
3 4 70
1 2 1
5 4 50
2 6 50
5 6 60
1 3 70
4 6 60
3 6 80
5 1 100
2 4 60
5 2 80

输出样例:

4 70

刚开始看这道题，我就感觉我要梦游了。噼里啪啦讲了一大堆，不知道讲了什么。。。
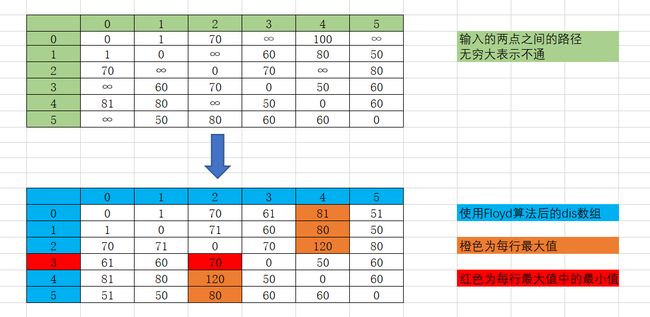
题目分析一下：每个动物都可以用咒语变成另一个动物，首先我们可以设两只动物直接的咒语当作是两地之间的距离保存起来。然后就是多源最短路（为什么是多源，因为你不知道那个起点最短，求得的结果就是最短的）。多源最短路用Floyd(弗洛伊德)算法。
求完之后，每行就是顶点i到各顶点j的最短距离，然后找出每行的最大值，再把所有行的最大值比较找出来那个最小的最大值以及其所在行。就找出来了从哪个顶点开始比较好。
特殊情况分析：题目上说，如果有一个动物无法变成其他所有动物，那就直接输出0。意思就是从一个地方，无论中间怎么转，都不能到达另一个地方，就输出0。

Floyd(弗洛伊德)算法5行核心代码

时间复杂度：O(N3)

void Floyd() 
{
	for (int k = 0; k < n; k++)  //k相当与中转点，比较经过中转点与原两点路程的大小，大舍小取
		//i,j表示循环二维数组
		for (int i = 0; i < n; i++)
			for (int j = 0; j < n; j++)
				if (dis[i][j] > dis[i][k] + dis[k][j])//比较大小，大舍小取
					dis[i][j] = dis[i][k] + dis[k][j];
}

实验代码

#include
#include
#include
using namespace std;
const int MAXV = 105;
const int INF = 0x3f3f3f3f;//表示无穷大

int n, m;//n为顶点数，m为边数
int dis[MAXV][MAXV];

//核心算法 - 弗洛伊德算法
void Floyd() 
{
	for (int k = 0; k < n; k++)  //k相当与中转点，比较经过中转点与原两点路程的大小，大舍小取
		//i,j表示循环二维数组
		for (int i = 0; i < n; i++)
			for (int j = 0; j < n; j++)
				if (dis[i][j] > dis[i][k] + dis[k][j])//比较大小，大舍小取
					dis[i][j] = dis[i][k] + dis[k][j];
}

//求每一行的最大值
int FindMaxDist(int i)
{
	int maxDist = 0;
	for (int j = 0; j < n; j++)
		if (dis[i][j] > maxDist)
			maxDist = dis[i][j];
	return maxDist;
}

int main()
{
	int u, v, w;
	int ans = 0, tmp, maxDist;

	//fill函数的作用是：将一个区间的元素都赋予val值。
	//函数参数：fill(vec.begin(), vec.end(), val); val为将要替换的值；
	fill(dis[0], dis[0] + MAXV * MAXV, INF);
	cin >> n >> m;

	for (int i = 0; i < n; i++)//自己到自己为0
		dis[i][i] = 0;
	for (int i = 0; i < m; i++)//输入长度
	{
		cin >> u >> v >> w;
		dis[u - 1][v - 1] = w;
		dis[v - 1][u - 1] = w;
	}

	Floyd();//求最短路径
	maxDist = INF;//无穷大
	for (int i = 0; i < n; i++)
	{
		tmp = FindMaxDist(i);//求每行最大值
		if (tmp < maxDist) 
		{
			maxDist = tmp;
			ans = i + 1;//下标从0开始，要+1
		}
	}

	if (ans == 0)//特殊情况
		cout << ans << endl;
	else
		printf("%d %d\n", ans, maxDist);

	return 0;
}