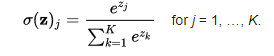独家 | 深度学习基础——激活函数以及什么时候使用它们？（附代码）

作者：Dishashree Gupta

翻译：王紫岳

校对：王琦

本文约5200字，建议阅读20分钟

本文简要介绍了作者在初次进行机器学习的操作时所遇到的情况与得到的教训。

摘要

• 激活函数是神经网络的组成部分之一。

• 学习深度学习中不同的激活函数。

• 在python中编写激活函数并在实时编码窗口中将结果可视化。

本文最初发表于2017年10月，并于2020年1月进行了更新，增加了三个新的激活函数和python代码。

引言

今天，因特网提供了获取大量信息的途径。无论我们需要什么，只需要谷歌搜索一下即可。然而，当我们获取了这么多的信息时，我们又面临着如何区分相关和无关的信息的挑战。

当我们的大脑被同时灌输大量信息时，它会努力去理解这些信息并将其分为“有用的”和“不那么有用的”。对于神经网络而言，我们需要类似的机制来将输入的信息分为“有用的”或“不太有用的”。

这是网络学习的重要方式，因为并不是所有的信息都同样有用。它们中的一些仅仅是噪音，而这就是激活函数的用武之地了。激活函数帮助神经网络使用重要信息，并抑制不相关的数据点。

接下来让我们来看看这些激活函数，了解它们是如何工作的，并找出哪些激活函数适合于什么样的问题情景。

目录

1. 神经网络概述

2. 我们可以不使用激活函数么？

3. 常用的激活函数以及什么时候使用他们

• Binary Step（二元阶跃）

• Linear（线性）

• Sigmoid（S型）

• Tanh（双曲正切）

• ReLU（线性整流单元）

• Leaky ReLU（泄露型线性整流函数）

• Parameterised ReLU（参数化线性整流函数）

• Exponential Linear Unit（指数化线性单元）

• Swish

• Softmax

4. 选择正确的激活函数

1. 神经网络概述

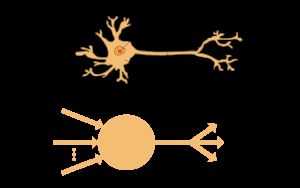
在我深入研究激活函数的细节之前，让我们先快速了解一下神经网络的概念以及它们是如何工作的。神经网络是一种非常强大的模仿人脑学习方式的机器学习机制。

大脑接收外界的刺激，对输入进行处理，然后产生输出。当任务变得复杂时，多个神经元形成一个复杂的网络，相互传递信息。

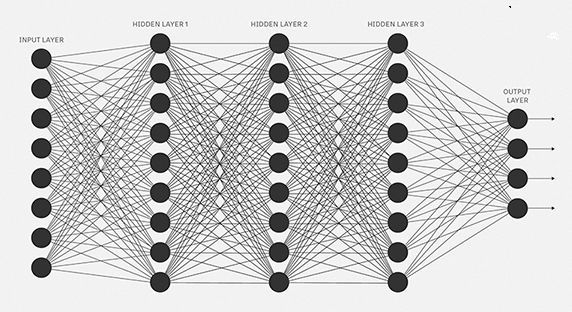
人工神经网络试图模仿类似的行为。你下面看到的网络是由相互连接的神经元构成的神经网络。每个神经元的特征是其权重、偏置和激活函数。

输入信息被输入到输入层，神经元使用权重和偏差对输入进行线性变换。

x = (weight * input) + bias

之后，对上述结果应用一个激活函数。

最后，激活函数的输出移动到下一个隐藏层，重复相同的过程。这种信息的前向移动称为前向传播。

如果生成的输出与实际值相距甚远怎么办?利用前向传播的输出来计算误差。根据这个误差值，更新神经元的权值和偏差。这个过程称为反向传播。

注:要详细理解正向传播和反向传播，您可以阅读下面的文章：

Understanding and coding neural network from scratch

附链接：https://www.analyticsvidhya.com/blog/2017/05/neural-network-from-scratch-in-python-and-r/

2. 我们可以不使用激活函数么?

我们知道，在正向传播期间，使用激活函数会在每一层引入一个额外的步骤。现在我们的问题是，假如激活函数给神经网络增加了复杂性，我们可以不使用激活函数吗?

想象一个没有激活函数的神经网络。在这种情况下，每个神经元只会利用权重和偏差对输入信息进行线性变换。虽然线性变换使神经网络更简单，但这个网络的功能会变得更弱，并无法从数据中学习复杂的模式。

没有激活函数的神经网络本质上只是一个线性回归模型。

因此，我们对神经元的输入进行非线性变换，而神经网络中的这种非线性是由激活函数引入的。

在下一节中，我们将研究不同类型的激活函数、它们的数学公式、图形表示和python代码。

3. 常用的激活函数以及什么时候使用他们

• 二元阶跃函数

当我们有一个激活函数时，首先想到的是一个基于阈值的分类器，即神经元是否应该根据线性变换的值被激活。

换句话说，如果激活函数的输入大于阈值，则神经元被激活，否则它就会失效，即它的输出不考虑下一个隐含层。让我们从数学的角度来看。

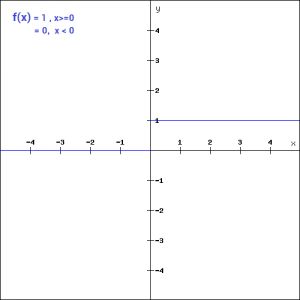
f(x) = 1, x>=0     
= 0, x<0

这是最简单的激活函数，可以用python中的一个if-else判断来实现

def binary_step(x):    
if x<0:        
return 0    
else:        
return 1binary_step(5), binary_step(-1)

输出：

(5,0)

在创建二分类器时，可以将二二元阶跃函数用作激活函数。可以想象，当目标变量中有多个类时，这个函数将会失效。这就是二元阶跃函数的局限性之一。

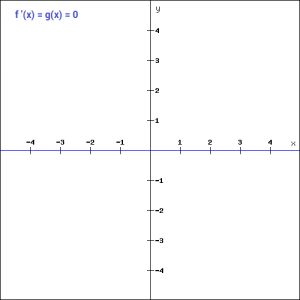
此外，阶跃函数的梯度为零，在反向传播过程中造成了障碍。也就是说，如果计算f(x)关于x的导数，结果是0。

f'(x) = 0, for all x

反向传播过程中的权重和偏差是通过计算梯度来更新的。因为函数的梯度是零，所以权值和偏差不会更新。

• Linear Function

在上面，我们看到了阶跃函数的问题是函数的梯度变成了0。这是由于在二元阶跃函数中没有x的分量，因此我们可以用线性函数代替二元函数。我们可以把这个函数定义为：

f(x)=ax

这里的活性值（activation）与输入成正比。本例中的变量“a”可以是任何常数值。让我们快速定义python中的函数:

def linear_function(x):
return 4*x linear_function(4), 
linear_function(-2)

输出：

(16, -8)

你认为这种情况下的导数是什么呢?当我们对函数关于x求导时，得到的结果将是x的系数，而这个系数是一个常数。

f'(x) = a

虽然这里的梯度不为零，但它是一个常数，与输入值x无关。这意味着权值和偏差在反向传播过程中会被更新，但更新因子是相同的。

在这种情况下，神经网络并不能真正改善误差，因为每次迭代的梯度是相同的。网络将不能很好地训练和从数据中捕获复杂的模式。因此，线性函数可能是需要高度解释能力的简单任务的理想选择。

• Sigmoid

我们要看的下一个激活函数是Sigmoid函数。它是应用最广泛的非线性激活函数之一。Sigmoid将值转换为0和1之间。这是sigmoid的数学表达式：

f(x) = 1/(1+e^-x)

这里值得注意的一点是，与二元阶跃和线性函数不同，sigmoid是一个非线性函数。

这本质上意味着，当我有多个神经元以sigmoid激活函数作为它们的激活函数时，它们的输出也是非线性的。下面是在python定义函数的python代码：

import numpy as np
def sigmoid_function
(x):    z = (1/(1 + np.exp(-x)))    
return z sigmoid_function(7),sigmoid_function(-22)

输出：

(0.9990889488055994, 2.7894680920908113e-10)

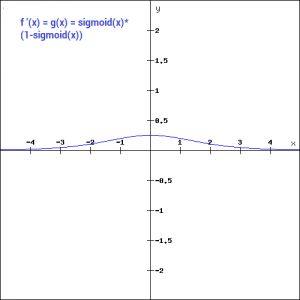
另外，正如你在上图中看到的，这是一个光滑的s型函数，并且是连续可微的。这个函数的导数是(1-sigmoid(x))。让我们来看看它的梯度图。

f'(x) = 1-sigmoid(x)

梯度值在-3和3范围内是显著的，但在其他区域，图形变得更平坦。这意味着对于大于3或小于-3的值，梯度非常小。当梯度值趋近于0时，网络就不是真的在学习。

另外，sigmoid函数不是关于0对称的。所以所有神经元的输出都是相同的符号。这可以通过缩放sigmoid函数来解决，这正是tanh函数所做的。请让我们继续读下去。

• Tanh

tanh函数与sigmoid函数非常相似。唯一不同的是它是关于原点对称的。本例中值的范围是从-1到1。因此，下一层的输入并不总是相同的符号。tanh函数定义为：

tanh(x)=2sigmoid(2x)-1

为了使用python编写代码，让我们简化前面的表达式。

tanh(x) = 2sigmoid(2x)-1
tanh(x) = 2/(1+e^(-2x)) -1

下面是它的python代码:

def tanh_function(x):    
z = (2/(1 + np.exp(-2*x))) -1
return z tanh_function(0.5), 
tanh_function(-1)

输出：

(0.4621171572600098, -0.7615941559557646)

 

就像你看到的，值的范围是-1到1。除此之外，tanh函数的其他性质都与sigmoid函数相同。与sigmoid相似，tanh函数在所有点上都是连续可微的。

我们来看看tanh函数的梯度。

与sigmoid函数相比，tanh函数的梯度更陡。你可能会好奇，我们如何决定选择哪个激活函数。通常tanh比sigmoid函数更受欢迎，因为它是以0为中心的，而且梯度不受一定方向的限制。

• ReLU

ReLU函数是另一个在深度学习领域得到广泛应用的非线性激活函数。ReLU表示线性整流单元（Rectified Linear Unit）。与其他激活函数相比，使用ReLU函数的主要优点是它不会同时激活所有神经元。

这意味着只有当线性变换的输出小于0时，神经元才会失效。下图将帮助你更好地理解这一点：

f(x)=max(0,x)

对于负的输入值，结果是零，这意味着神经元没有被激活。由于只有一定数量的神经元被激活，ReLU函数的计算效率远高于sigmoid和tanh函数。下面是ReLU的python函数:

def relu_function(x):    
if x<0:        
return 0    
else:        
return x relu_function(7), relu_function(-7)

输出：

(7, 0)

我们来看看ReLU函数的梯度。

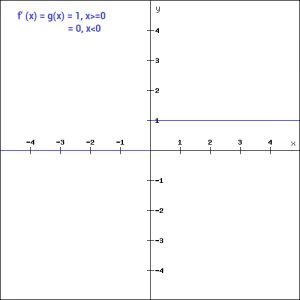
f'(x) = 1, x>=0      
= 0, x<0

如果你观察图形的负方向，你会注意到梯度值是零。由于这个原因，在反向传播过程中，一些神经元的权重和偏差没有更新。这可能会产生从未被激活的死亡神经元。这种情况可通过“泄漏”ReLU函数来处理。

• Leaky ReLU

Leaky ReLU函数只是ReLU函数的一个改进版本。如我们所见，对于ReLU函数，当x<0时，梯度为0，这将使该区域的神经元失活。

定义Leaky ReLU是为了解决这个问题。我们不把x的负值定义为0，而是定义为x的一个极小的线性分量，这里给出它的数学定义：

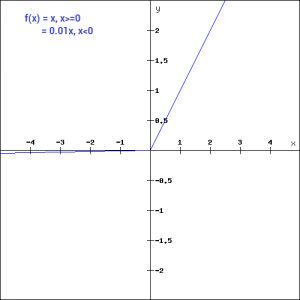
f(x)= 0.01x, x<0    
=   x, x>=0

通过这个小的修改，图形左边的梯度就变成了一个非零值。因此，我们将不再在那个区域遇到死亡的神经元。这是Leaky ReLU函数的导数：

f'(x) = 1, x>=0
     =0.01, x<0

因为Leaky ReLU是ReLU的一个变体，所以python代码可以通过一个小的修改来实现：

def leaky_relu_function(x):   
if x<0:        
return 0.01*x    
else:        
return x leaky_relu_function(7), leaky_relu_function(-7)

输出：

(7, -0.07)

除了Leaky ReLU，还有一些其他的ReLU变体，最流行的是Parameterised ReLU函数和Exponential Liner Unit。

• Parameterised ReLU

这是ReLU的另一个变体，旨在解决轴的左半部分的梯度为零的问题。顾名思义，参数化ReLU引入了一个新参数作为函数负部分的斜率。下面是如何修改ReLU函数以体现包含的斜率参数-

f(x) = x, x>=0    
= ax, x<0

当a的值固定为0.01时，函数就变成了Leaky ReLU函数。然而，对于Parameterised ReLU函数，‘a’也是一个可训练的参数。该网络还学习了' a '的值，以便更快、更优地收敛。

这个函数的导数和Leaky ReLu函数是一样的，除了0.01的值会被替换成a的值。

f'(x) = 1, x>=0       
= a, x<0

当使用Leaky ReLU函数仍然不能解决未激活神经元问题，相关信息无法成功传递到下一层时，我们就可以使用Parameterised ReLU函数。

• Exponential Linear Unit

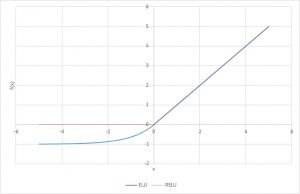
指数化线性单元(简称ELU)也是线性整流单元(ReLU)的一种变体，它改变了函数负部分的斜率。与Leaky Relu和parametric Relu函数不同，ELU使用了Log曲线来代替直线定义函数的负数部分。它被定义为

f(x) = x,   x>=0    
= a(e^x-1), x<0

让我们在python中定义这个函数：

def elu_function(x, a):    
if x<0:        
return a*(np.exp(x)-1)    
else:        
return x elu_function(5, 0.1),elu_function(-5, 0.1)

输出：

(5, -0.09932620530009145)

ELU函数对于x大于0的值的导数是1，就像所有ReLU变体一样。但对于x<0的值，导数是a.e ^x 。

f'(x) = x,   x>=0    
= a(e^x), x<0

• Swish

Swish是一个不太为人所知的激活函数，它是由谷歌的研究人员发现的。Swish的计算效率与ReLU相当，并且在层次更深的模型上显示出比ReLU更好的性能。swish的值从负无穷到正无穷。函数定义为-

f(x) = x*sigmoid(x)
f(x) = x/(1-e^-x)

正如你所看到的，函数曲线是平滑且在所有点上都是可微的。这在模型优化过程中是有帮助的，也是Swish被认为优于Relu的原因之一。

关于这个函数的一个独特的特征是，swich函数不是单调的。这意味着即使输入值增加，函数值也可能减少。让我们看看swish函数的python代码：

def swish_function(x):    
return x/(1-np.exp(-x)) 
swish_function(-67), swish_function(4)

输出：

(5.349885844610276e-28, 4.074629441455096)

• Softmax

Softmax函数通常被描述为多个sigmoid的组合。我们知道sigmoid返回0到1之间的值，可将函数值视为数据点属于特定类的概率。因此，sigmoid被广泛应用于二分类问题。

softmax函数可用于多类分类问题。这个函数返回属于每个类的数据点的概率。这是相同的数学表达式：

在为一个多类问题构建神经网络时，输出层的神经元数量与目标中的类的数量相同。

例如，如果你有三个类，在输出层会有三个神经元。假设神经元的输出是[1.2,0.9,0.75]。

对这些值应用softmax函数，您将得到以下结果—[0.42,0.31,0.27]。这些值表示这些数据点属于每个类的概率。值得注意的是，所有值的和为1。让我们在python中编码：

def softmax_function(x):    
z = np.exp(x)    
z_ = z/z.sum()    
return z_ 
softmax_function([0.8, 1.2, 3.1])

输出：

softmax_function([1.2 , 0.9 , 0.75])

4.选择正确的激活函数

现在我们已经看到了这么多的激活函数，我们需要一些逻辑/启示来了解在什么情况下应该使用哪个激活函数。好或坏的判断并没有经验法则。

然而，根据问题的性质，我们可以做出更好的选择，使网络更容易、更快地收敛。

• 对于分类器，Sigmoid函数及其组合通常工作得更好。

• 由于有梯度消失的问题，有时会避免使用sigmoid和tanh函数。

• ReLU函数是一种通用的激活函数，目前被广泛使用。

• 如果在我们的网络中遇到神经元未激活的情况，Leaky ReLU函数是最好的选择。

• 始终记住，ReLU函数应该只在隐藏层中使用。

• 根据经验，您可以从使用ReLU函数开始，然后在ReLU不能提供最佳结果的情况下转移到其他激活函数。

 

项目

现在，是时候冒险尝试一下其他真实的数据集了。那么你准备好接受挑战了吗?通过以下实践问题加速你的深度学习之旅:

l Practice Problem: Identify the Apparels(见下面链接)

https://datahack.analyticsvidhya.com/contest/practice-problem-identify-the-apparels/?utm_source=fundamentals-deep-learning-activation-functions-when-to-use-them&utm_medium=blog

l Practice Problem: Identify the Digits（见下面链接）

https://datahack.analyticsvidhya.com/contest/practice-problem-identify-the-digits/?utm_source=fundamentals-deep-learning-activation-functions-when-to-use-them&utm_medium=blog

 

结语：在本文中，我讨论了各种类型的激活函数，以及在使用它们时可能遇到的问题类型。我建议你先从ReLU函数开始，并随着你慢慢深入时，探索其他函数。你还可以设计自己的激活函数，为你的神经网络提供一个非线性组件。如果您使用了自己的激活函数并且效果非常好，请与我们分享，我们将很乐意将其纳入列表。

 

原文链接： 

https://www.analyticsvidhya.com/blog/2020/01/fundamentals-deep-learning-activation-functions-when-to-use-them/

原文标题：

Fundamentals of Deep Learning – Activation Functions and When to Use Them?

编辑：王菁

校对：林亦霖

译者简介

王紫岳，悉尼大学Data Science在读研究生，在数据科学界努力奋斗的求知者。喜欢有挑战性的工作与生活，喜欢与朋友们热切交谈，喜欢在独处的时候读书品茶。张弛有度，才能够以最饱满的热情迎接有点忙碌的生活。

翻译组招募信息

工作内容：需要一颗细致的心，将选取好的外文文章翻译成流畅的中文。如果你是数据科学/统计学/计算机类的留学生，或在海外从事相关工作，或对自己外语水平有信心的朋友欢迎加入翻译小组。

你能得到：定期的翻译培训提高志愿者的翻译水平，提高对于数据科学前沿的认知，海外的朋友可以和国内技术应用发展保持联系，数据派产学研的背景为志愿者带来好的发展机遇。

其他福利：来自于名企的数据科学工作者，北大清华以及海外等名校学生他们都将成为你在翻译小组的伙伴。

点击文末“阅读原文”加入数据派团队~

转载须知

如需转载，请在开篇显著位置注明作者和出处（转自：数据派ID：DatapiTHU），并在文章结尾放置数据派醒目二维码。有原创标识文章，请发送【文章名称-待授权公众号名称及ID】至联系邮箱，申请白名单授权并按要求编辑。

发布后请将链接反馈至联系邮箱（见下方）。未经许可的转载以及改编者，我们将依法追究其法律责任。

点击“阅读原文”拥抱组织