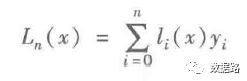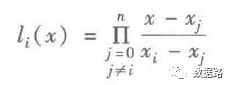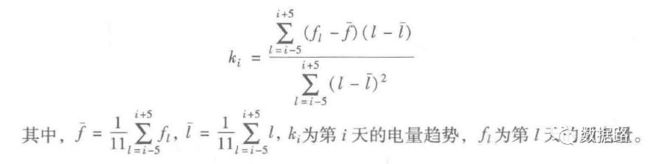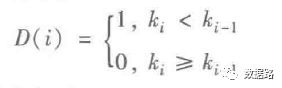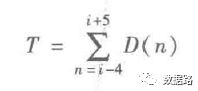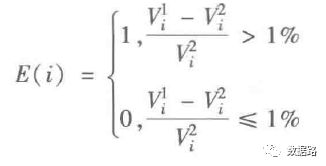手把手实战:利用LM神经网络算法自动识别窃电用户(附代码)
![]()
来源:数据路
本文约3000字,建议阅读7分钟。
通过本文给大家介绍利用LM神经网络算法进行电力窃漏电用户的自动识别。
背景与挖掘目标
背景
传统的防窃漏电方法主要通过定期巡检、定期校验电表、用户举报窃电等方法来发现窃电或计量装置故障。
但这种方法对人的依赖性太强,抓窃查漏的目标不明确。
通过采集电量异常、负荷异常、终端报警、主站报警、线损异常等信息,建立数据分析模型,来实时监测窃漏电情况和发现计量装置的故障。
目标
归纳出窃漏电用户的关键特征,构建窃漏电用户的识别模型。
利用实时检测数据,调用窃漏电用户识别模型实现实时诊断。
分析方法与过程
分析方法
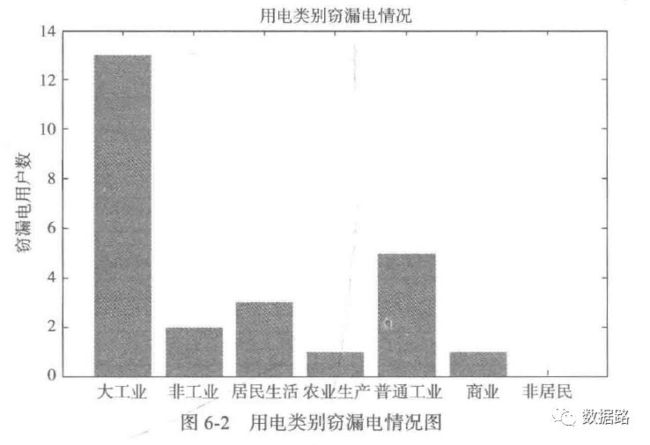
窃漏电用户在电力计量自动化系统的监控大用户中只占一小部分,同时某些大用户也不可能存在窃漏电行为,如银行、税务、学校和工商等非居民类别,故在数据预处理时有必要将这些类别用户剔除。
系统中的用电负荷不能直接体现出用户的窃漏电行为,终端报警存在很多误报和漏报的情况,故需要进行数据探索和预处理,总结窃漏电用户的行为规律,再从数据中提炼出描述窃漏电用户的特征指标。
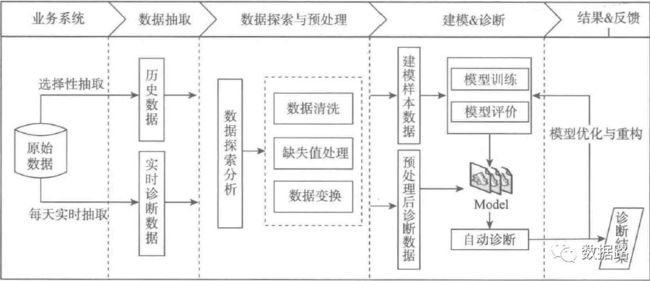
最后结合历史窃漏电用户信息,整理出识别模型的专家样本数据集,再进一步构建分类模型,实现窃漏电用户的自动识别。窃漏电用户识别流程如图6.1所示,主要包話以下步骤。
过程整理
从电力计量自动化系统、营销系统有选择性地抽取部分大用户用电负荷、终端报警及违约窃电处罚信息等原始数据。
对样本数据探索分析,剔除不可能存在窃漏电行为行业的用户,即白名单用户,初步审视正常用户和窃漏电用户的用电特征。
对样本数据进行预处理,包括数据清洗、缺失值处理和数据变换。
构建专家样本集。
构建窃漏电用户识别模型。
在线监测用户用电负荷及终端报警,调用模型实现实时诊断。
数据探索分析
以下代码可以使用Excel直接打开数据集,进行画图分析。
1. 分布分析
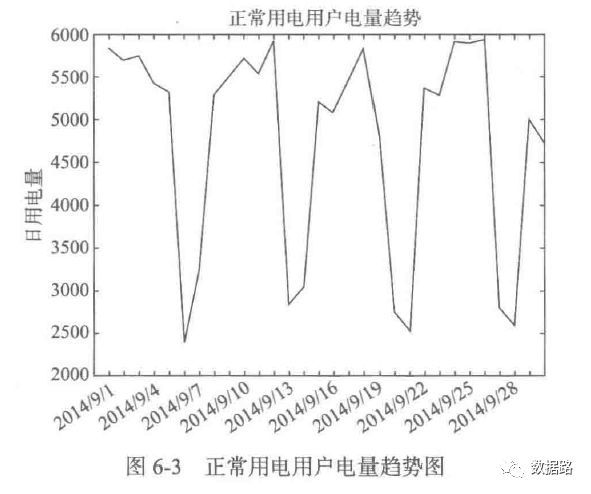
2. 周期性分析
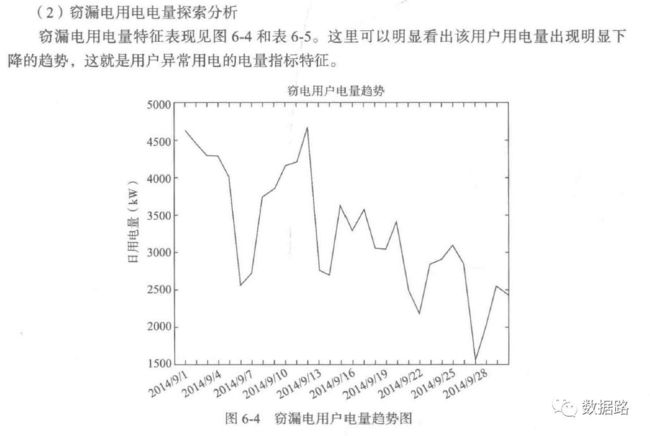
3. 窃漏电用电电量分析
数据预处理
1. 数据清洗
非居民不存在透漏电,如学校,邮局等等
结合业务,节假日会比平时偏低,为了达到更好效果,去处掉节假日。
2. 缺失值处理
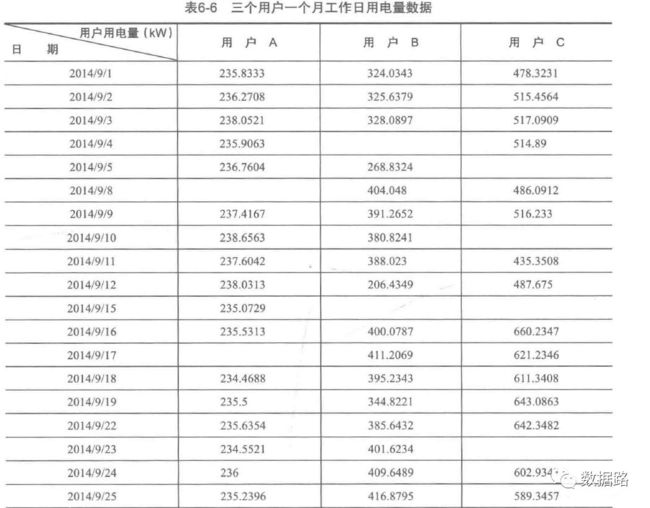
具体见数据集内容对于缺失值处理,采用拉格朗日插值法补值,具体方法如下。
首先,确定原始数据集中的自变量和因变量,
取出缺失值前后五个数据(空值和不存在,去掉)
取出十个数据为一组,采用拉格朗日多项式差值公式
#-*- coding: utf-8 -*-
#拉格朗日插值代码
import pandas as pd #导入数据分析库Pandas
from scipy.interpolate import lagrange #导入拉格朗日插值函数
inputfile = '/home/kesci/input/date14037/missing_data.xls' #输入数据路径,需要使用Excel格式;
outputfile = '/home/kesci/work/missing_data_processed.xls' #输出数据路径,需要使用Excel格式,这里在科赛上,所以本地运行需要修改路径
data = pd.read_excel(inputfile, header=None) #读入数据
print(data)
#自定义列向量插值函数
#s为列向量,n为被插值的位置,k为取前后的数据个数,默认为5
def ployinterp_column(s, n, k=5):
y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))] #取数,注意这类()取最左,不取最右。
y = y[y.notnull()] #剔除空值
return lagrange(y.index, list(y))(n) #插值并返回插值结果
#逐个元素判断是否需要插值
for i in data.columns:
for j in range(len(data)):
if (data[i].isnull())[j]: #如果为空即插值。
data[i][j] = ployinterp_column(data[i], j)
print(data)
data.to_excel(outputfile, header=None, index=False) #输出结果
0 1 2
0 235.8333 324.0343 478.3231
1 236.2708 325.6379 515.4564
2 238.0521 328.0897 517.0909
3 235.9063 NaN 514.8900
4 236.7604 268.8324 NaN
5 NaN 404.0480 486.0912
6 237.4167 391.2652 516.2330
7 238.6563 380.8241 NaN
8 237.6042 388.0230 435.3508
———————————数据处理前后————————————
0 1 2
0 235.833300 324.034300 478.323100
1 236.270800 325.637900 515.456400
2 238.052100 328.089700 517.090900
3 235.906300 203.462116 514.890000
4 236.760400 268.832400 493.352591
5 237.151181 404.048000 486.091200
6 237.416700 391.265200 516.233000
7 238.656300 380.824100 493.342382
8 237.604200 388.023000 435.350800
数据变换
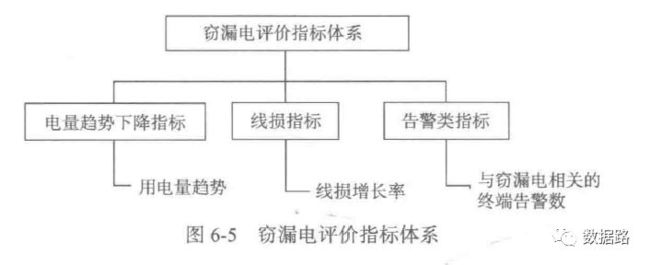
通过电力计量系统采集的电量、负荷,虽然在一定程度上能反映用户窃漏电行为的某些规律,但要作为构建模型的专家样本,特征不明显,需要进行重新构造。基于数据变换,得到新的评价指标来表征窃漏电行为所具有的规律,其评价指标体系如图6巧所示。
用电量趋势下降指标
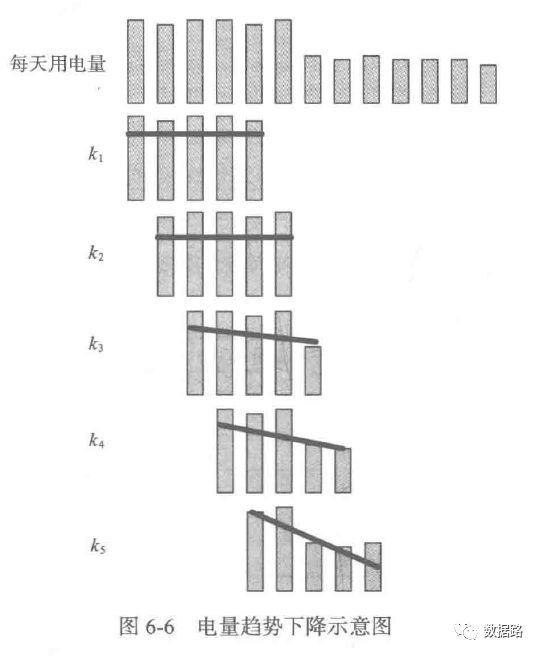
由之前的周期性分析,可以发现。窃漏电用户的用电量,会不断呈下降态势。然后趋于平缓。正常用户,整体上呈平稳态势。所以,考虑用一段时间的用电量拟合成一条直线,判断斜率进行指标计算。
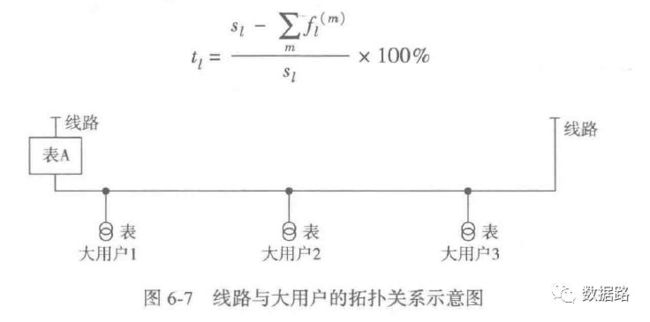
线损指标
综上指标计算方法,得出数据,详情看数据集中的model.xls你要问我怎么数字计算。我也很懵呀,找个机会把数学公式计算办法学习完后,再来补充相应的代码但是,我觉得可以用excel比较简单的较快处理这些数据。训练用的专家样本数据看附件中的model.xls
模型构建
1. 构建窃漏电用户识别模型
数据划分
对专家样本,随机选取20%作为测试样本,80%作为训练样本,代码如下
LM神经网络
使用Keras库为我们建立神经网络模型,设定KM神经网络的输入节点数为3,输出节点为1,隐藏节点数为10,使用Adam方法求解,隐藏层使用Relu(x)=max(x,0)作为激活函数,实验表面该函数能大幅提高模型的准确率。
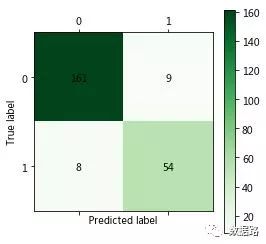
以下代码运行需要两三分钟时间,运行完毕后,得到混淆矩阵图。可以算得,分类准确率为(161+58)/(161+58+6+7)=94.4%,正常的用户被误判为窃漏电用户占正常的7/(161+7)=4.2%,窃漏电用户被误判为正常用户占正常用户的6/(6+58)=9.4%。
#-*- coding: utf-8 -*-
import matplotlib.pyplot as plt
import pandas as pd
from random import shuffle
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
cm = confusion_matrix(y, yp) #混淆矩阵
import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() #颜色标签
for x in range(len(cm)): #数据标签
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
return plt
datafile = '/home/kesci/input/date14037/model.xls'
data = pd.read_excel(datafile)
data = data.as_matrix()
shuffle(data)
p = 0.8 #设置训练数据比例
train = data[:int(len(data)*p),:]#多维数据的切片方法
test = data[int(len(data)*p):,:]#逗号左边,代表行,右边代表列
#构建LM神经网络模型
from keras.models import Sequential #导入神经网络初始化函数
from keras.layers.core import Dense, Activation #导入神经网络层函数、激活函数
netfile = '/home/kesci/input/date14037/net.model' #构建的神经网络模型存储路径
net = Sequential() #建立神经网络
net.add(Dense(input_dim = 3, output_dim = 10)) #添加输入层(3节点)到隐藏层(10节点)的连接
net.add(Activation('relu')) #隐藏层使用relu激活函数
net.add(Dense(input_dim = 10, output_dim = 1)) #添加隐藏层(10节点)到输出层(1节点)的连接
net.add(Activation('sigmoid')) #输出层使用sigmoid激活函数
net.compile(loss = 'binary_crossentropy', optimizer = 'adam') #编译模型,使用adam方法求解
net.fit(train[:,:3], train[:,3], nb_epoch=100, batch_size=1) #训练模型,循环1000次,不用于书籍源代码,这里需要删除class这个值才能正常运行
net.save_weights(netfile) #保存模型
predict_result = net.predict_classes(train[:,:3]).reshape(len(train)) #预测结果变形
'''这里要提醒的是,keras用predict给出预测概率,predict_classes才是给出预测类别,而且两者的预测结果都是n x 1维数组,而不是通常的 1 x n'''
#导入自行编写的混淆矩阵可视化函数,具体见最上代码 cm_plot(y, yp)
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
cm = confusion_matrix(y, yp) #混淆矩阵
import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() #颜色标签
for x in range(len(cm)): #数据标签
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
return plt
cm_plot(train[:,3], predict_result).show() #显示混淆矩阵可视化结果
from sklearn.metrics import roc_curve #导入ROC曲线函数
predict_result = net.predict(test[:,:3]).reshape(len(test))
fpr, tpr, thresholds = roc_curve(test[:,3], predict_result, pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of LM') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例
plt.show() #显示作图结果
模型评价与分析:LM神经网络使用Keras库为我们建立神经网络模型,设定KM神经网络的输入节点数为3,输出节点为1,隐藏节点数为10,使用Adam方法求解,隐藏层使用Relu(x)=max(x,0)作为激活函数,实验表面该函数能大幅提高模型的准确率。
以上代码运行需要两三分钟时间,运行完毕后,得到混淆矩阵图。可以算得,分类准确率为(161+58)/(161+58+6+7)=94.4%,正常的用户被误判为窃漏电用户占正常的7/(161+7)=4.2%,窃漏电用户被误判为正常用户占正常用户的6/(6+58)=9.4%。
CART决策树算法
#-*- coding: utf-8 -*-
#构建并测试CART决策树模型
import pandas as pd #导入数据分析库
from random import shuffle #导入随机函数shuffle,用来打算数据
datafile = '/home/kesci/input/date14037/model.xls' #数据名
data = pd.read_excel(datafile) #读取数据,数据的前三列是特征,第四列是标签
data = data.as_matrix() #将表格转换为矩阵
shuffle(data) #随机打乱数据
p = 0.8 #设置训练数据比例
train = data[:int(len(data)*p),:] #前80%为训练集
test = data[int(len(data)*p):,:] #后20%为测试集
#构建CART决策树模型
from sklearn.tree import DecisionTreeClassifier #导入决策树模型
treefile = '/home/kesci/work/tree.pkl' #模型输出名字
tree = DecisionTreeClassifier() #建立决策树模型
tree.fit(train[:,:3], train[:,3]) #训练
#保存模型
from sklearn.externals import joblib
joblib.dump(tree, treefile)
#导入自行编写的混淆矩阵可视化函数
def cm_plot(y, yp):
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
cm = confusion_matrix(y, yp) #混淆矩阵
import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() #颜色标签
for x in range(len(cm)): #数据标签
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
return plt
cm_plot(train[:,3], tree.predict(train[:,:3])).show() #显示混淆矩阵可视化结果
#注意到Scikit-Learn使用predict方法直接给出预测结果。
from sklearn.metrics import roc_curve #导入ROC曲线函数
fpr, tpr, thresholds = roc_curve(test[:,3], tree.predict_proba(test[:,:3])[:,1], pos_label=1)
plt.plot(fpr, tpr, linewidth=2, label = 'ROC of CART', color = 'green') #作出ROC曲线
plt.xlabel('False Positive Rate') #坐标轴标签
plt.ylabel('True Positive Rate') #坐标轴标签
plt.ylim(0,1.05) #边界范围
plt.xlim(0,1.05) #边界范围
plt.legend(loc=4) #图例
plt.show() #显示作图结果
运行结果如下:
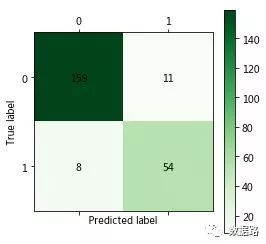
模型评价与分析:分类的准确率为(160+56)/(160+56+3+13)=93.1%,得到的混淆矩阵如上。因为每次随机的样本不同,随意准确率是在一定区间内浮动。
模型对比评价
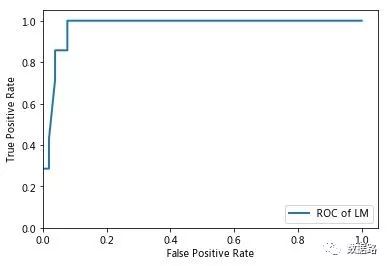
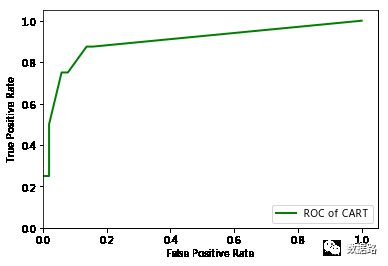
采用OCR曲线评价方法进行评估,一个优秀的分类器所对应的ROC曲线应该是尽量靠近左上角的。
通过对比,可以比较容易得出,LM神经网络的ROC曲线更加符合优秀的定义。说明LM神经网络模型的分类性能较好,能应用于窃漏电用户识别。
进行窃漏电诊断
在线监测用户用电负荷及终端报警数据,并利用经过2.3节的处理所得到模型,输入在线实时数据,再利用前面代码构建好的窃漏电用户识别模型计算用户的窃漏电诊断结果,实现了窃漏电用户实时诊断。
小结
了解了数据挖掘算法中LM神经网络和CART决策树算法的实际应用场景
但是还未深刻理解,这个两个算法背后原理,往后在学习《数据挖掘导论》时要理解。
了解了识别模型优劣中的ROC比较方法,但是应该还会有更好的方式。
这个案例,可以类推到汽车相关的偷漏税项目上。但是,自己实战时发现,目标原始数据很难去发现有效指标与建立评价指标,业务的理解转换能力不足
目前,还在同步学习秦路的《七周数据分析师》希望能获得一些业务能力,帮助项目进行。
![]()