图像可形变配准的Demons方法

图像的可形变配准分为参数法和非参数法，参数法例如仿射变换、B-spline based FFD等方法通过对形变的参数化表示，减小求解的变量个数，但是也限制了形变复杂程度。非参数化的方法将图像的形变表示成位移场，每一个像素都有一个位移，可以表示更加复杂的形变，但是要求解的变量也更多。

1, Thirion’s Demons

Demons就是一种著名的非参数化可形变配准方法。它最早来自于光流算法(optical flow),光流是用来估计视频图像中相邻的两帧图像目标的位移，也就是目标移动的速度，其基本方程为

v=(s−m)∇s|∇s|2 (公式1)

其中 s 是第一帧图像， m 是第二帧图像。

光流算法有两个基本假设：1， 相邻两帧图像中目标的灰度值不变。2， 相邻两帧之间目标的位移比较小。

在图像配准中， s 也叫做静止图像， m 也叫作移动图像。配准的目标是找到一个从 s 到 m 的变换以确定像素之间的对应关系。Thirion将光流算法引入到图像配准中，为了防止图像梯度为0时计算出现问题，在分母中加了一项图像灰度差：

u=(s−m)∇s|∇s|2+(s−m)2 (公式2)

该公式得到一个小的位移量，在Demons算法中，通过该公式的多次迭代并且用高斯滤波器对位移场进行平滑处理，得到配准所需的变化。其基本代码如下：

S=im2double(imread('images/lenag2.png')); % static image
M=im2double(imread('images/lenag2.png')); % moving image
% The transformation fields
Tx=zeros(size(M)); Ty=zeros(size(M));
for itt=1:200
        % Difference image between moving and static image
        Idiff=M-S;

        % Default demon force, (Thirion 1998)
        Ux = -(Idiff.*Sx)./((Sx.^2+Sy.^2)+Idiff.^2);
        Uy = -(Idiff.*Sy)./((Sx.^2+Sy.^2)+Idiff.^2);

        % When divided by zero
        Ux(isnan(Ux))=0; Uy(isnan(Uy))=0;

        % Smooth the transformation field
        Uxs=3*imfilter(Ux,Hsmooth);
        Uys=3*imfilter(Uy,Hsmooth);

        % Add the new transformation field to the total transformation field.
        Tx=Tx+Uxs;
        Ty=Ty+Uys;
        M=movepixels(I1,Tx,Ty); 
end

2, Wang’s Demons
Thirion’s Demons 只使用了静止图像的梯度计算形变的力（即 u⃗  ），为了使配准过程更快，Wang’s Demons既使用静止图像的梯度，也使用运动图像的梯度来定义形变力。

u⃗ =(s−m)×(∇s|∇s|2+α2(s−m)2+∇m|∇m|2+α2(s−m)2) (公式3)

通过使用静止图像和运动图像两方面的力，算法可以收敛的更快。其中 α 是在[P. Cachier 1999]提出来的。根据平方不等式

|∇s|2+α2(s−m)2≥2α(s−m)|∇s|) (公式4)

可以知道 u⃗  的上限为 1/α ,因此可以通过设置 α 的值来调节形变的幅度,可以在最初的几次迭代中使用较小的 α ，随着迭代次数的增加，使用大一点的 α 。
该算法的实例代码为：

S=im2double(imread('images/lenag2.png')); % static image
M=im2double(imread('images/lenag2.png')); % moving image
% The transformation fields
Tx=zeros(size(M)); Ty=zeros(size(M));
for itt=1:200
        % Difference image between moving and static image
        Idiff=M-S;

        % Default demon force, (Thirion 1998)
        % Ux = -(Idiff.*Sx)./((Sx.^2+Sy.^2)+Idiff.^2);
        % Uy = -(Idiff.*Sy)./((Sx.^2+Sy.^2)+Idiff.^2);

        % Extended demon force. With forces from the gradients from both
        % moving as static image. (Cachier 1999, He Wang 2005)
        [My,Mx] = gradient(M);
        Ux = -Idiff.*  ((Sx./((Sx.^2+Sy.^2)+alpha^2*Idiff.^2))+(Mx./((Mx.^2+My.^2)+alpha^2*Idiff.^2)));
        Uy = -Idiff.*  ((Sy./((Sx.^2+Sy.^2)+alpha^2*Idiff.^2))+(My./((Mx.^2+My.^2)+alpha^2*Idiff.^2)));

        % When divided by zero
        Ux(isnan(Ux))=0; Uy(isnan(Uy))=0;

        % Smooth the transformation field
        Uxs=3*imfilter(Ux,Hsmooth);
        Uys=3*imfilter(Uy,Hsmooth);

        % Add the new transformation field to the total transformation field.
        Tx=Tx+Uxs;
        Ty=Ty+Uys;
        M=movepixels(I1,Tx,Ty); 
end

3, 从数学的方式来理解Demons

上述方法都是启发式的算法，而没有理论上的数学模型。如果从数学上来推导，能给Demons一个理论解释。

[Vecauteren 2007]给出了一个标准的配准模型：配准的能量函数包括相似性测度和对位移场的平滑化限制。

E(u)=||s−m∘(t+u)||2+σ2iσ2x||u||2 (公式5)

其中t是要求解的形变位移，而 u 是每一次迭代过程中 t 的增量。 ∘ 代表对图像的变换。 σi 和 σx 分别代表灰度不确定性（图像噪声）和变换不确定性。

如果将根据当前形变参数 t 变换后的运动图像重新表示为 m∘t ，在求新的 u 时的能量函数可以表示为

E(u)=||s−m∘t+uJu||2+σ2iσ2x||u||2 (公式6)

相应的导数为

∇E(u)=−2(Ju)T(s−m∘t+uJu)+2σ2iσ2xu (公式7)

其中 Ju 是静止图像或者移动图像的梯度，令 ∇E(u)=0 ,则得到当前迭代步骤中 u 的值为

u=s−m∘t||Ju||2+σ2iσ2xJu (公式8)

如果令 σi=|s−m| , σx=1/α ，可得:

u=s−m∘t||Ju||2+α2(s−m∘t)2Ju (公式9)

对 Ju 可以进行不同的定义，例如 Ju=∇f , Ju=∇(m∘t) , 或者 Ju=(∇s+∇(m∘t))/2 , 这三个梯度公式分别对应Gauss-Newton法，Thirion’s rule和ESM（Efficient second-order Minimization）法，得到的结果分别为

u=s−m∘t||∇f||2+α2(s−m∘t)2∇s (公式10)

u=s−m∘t||∇m||2+α2(s−m∘t)2∇m （公式11）

u=2s−m∘t||∇s+∇(m∘t||2+α2(s−m∘t)2(∇s+∇(m∘t) (公式12)

4, Inertial Demons
Inertial Demons就是在每一次计算 t 的增量 u 时,不仅考虑当前的u，也考虑上一次迭代的 u ，相当于引入一个动量，可以将 u 理解为速度，那么考虑到惯性，当前时刻是速度会保持一部分上一时刻的速度。在公式（3）的基础上使用动量，则
u(n+1)=βu(n)+(s−m)×(∇s|∇s|2+α2(s−m)2+∇m|∇m|2+α2(s−m)2)

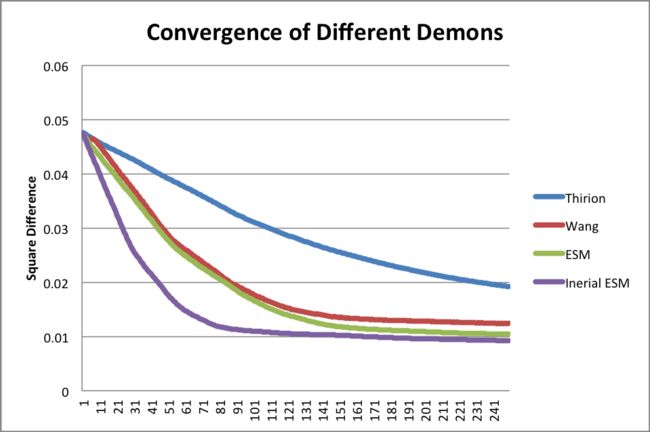
下图是使用Inertial Demons的配准结果（ α=2.0,β=0.5 ）：

下图是使用不同的Demons方法收敛速度的比较：

参考文章
[1] J.P. Thirion, “Image matching as a diffusion process: an analogy with maxwell’s demons,” Medical Image Analysis, 1998.
[2] H. Wang, et al. “Validation of an accelerated ’demons’ algorithm for deformable image registration in radiation therapy,” Physics in
Medicine and Biology, 2005.
[3] T. Vercauteren, et al. “Nonparametric diffeomorphic image registration with the demons algorithm,” MICCAI 2007
[4] A. Santos-Ribeiro, et al. “Inertial Demons : A Momentum-Based Diffeomorphic Registration Framework”, MICCAI 2016
[5] Vercauteren, Tom, et al. “Insight into efficient image registration techniques and the demons algorithm.” BICIPMI 2007.
[6] 示例代码在这里下载。