- matlab mle 优化,MLE+: Matlab Toolbox for Integrated Modeling, Control and Optimization for Buildings...
Simon Zhong
matlabmle优化
摘要:FollowingunilateralopticnervesectioninadultPVGhoodedrat,theaxonguidancecueephrin-A2isup-regulatedincaudalbutnotrostralsuperiorcolliculus(SC)andtheEphA5receptorisdown-regulatedinaxotomisedretinalgan
- 【论文速读】| SEAS:大语言模型的自进化对抗性安全优化
云起无垠
论文速读/精读语言模型安全人工智能
本次分享论文:SEAS:Self-EvolvingAdversarialSafetyOptimizationforLargeLanguageModels基本信息原文作者:MuxiDiao,RumeiLi,ShiyangLiu,GuogangLiao,JingangWang,XunliangCai,WeiranXu作者单位:北京邮电大学,美团关键词:大语言模型(LLM),对抗安全,红队,模型优化,自
- Hexagon_DSP_User_Guide(2)
weixin_38498942
tools简介dsp开发开发语言tool
Hexagon_DSP_User_Guide(2)4.2Guidelinesforassemblyandintrinsicoptimization4.2.1Maximizeinstructionsperpacket4.2.1.1Scalarinstructionpackingrules4.2.1.2HVXpackingrules4.2.2Understandandreducestalls4.2.2
- DAG (directed acyclic graph) 作为大数据执行引擎的优点
joeywen
分布式计算StormSparkStorm杂谈StormsparkDAG
TL;DR-ConceptuallyDAGmodelisastrictgeneralizationofMapReducemodel.DAG-basedsystemslikeSparkandTezthatareawareofthewholeDAGofoperationscandobetterglobaloptimizationsthansystemslikeHadoopMapReducewhicha
- 【论文简介】Circle Loss: A Unified Perspective of Pair Similarity Optimization
萝莉狼
machinelearningcirclelossdeepfeaturelearning
CircleLoss:AUnifiedPerspectiveofPairSimilarityOptimization旷世cvpr2020的一篇文章,站在更高的视角,统一了deepfeaturelearning的两大基础loss:基于class-levellabel的loss(如softmax+crossentropy)和基于pair-wiselabel的loss(如tripletloss),指出了
- Circle Loss: A Unified Perspective of Pair Similarity Optimization简要阅读笔记
dailleson_
机器学习机器学习数据挖掘神经网络深度学习自然语言处理
1.背景常见的分类损失函数可以概括为减小类内距离sns_nsn,增大类间距离sps_psp。优化目标如下:min(sn−sp)min(s_n-s_p)min(sn−sp)2.存在的问题优化不够灵活。优化目标对sns_nsn和sps_psp的惩罚作用是相等的,二者的系数都为1。例如{sn,sp}={0.1,0.5}\{s_n,s_p\}=\{0.1,0.5\}{sn,sp}={0.1,0.5}。这个
- [论文笔记]Circle Loss: A Unified Perspective of Pair Similarity Optimization
愤怒的可乐
#文本匹配[论文]论文翻译/笔记自然语言处理论文阅读人工智能
引言为了理解CoSENT的loss,今天来读一下CircleLoss:AUnifiedPerspectiveofPairSimilarityOptimization。为了简单,下文中以翻译的口吻记录,比如替换"作者"为"我们"。这篇论文从对深度特征学习的成对相似度优化角度出发,旨在最大化同类之间的相似度sps_ps
- 探索智能边缘计算:Game-Theoretic-Deep-Reinforcement-Learning
瞿旺晟
探索智能边缘计算:Game-Theoretic-Deep-Reinforcement-LearningGame-Theoretic-Deep-Reinforcement-LearningCodeofPaper"JointTaskOffloadingandResourceOptimizationinNOMA-basedVehicularEdgeComputing:AGame-TheoreticDRL
- 大模型对齐方法笔记一:DPO及其变种IPO、KTO、CPO
chencjiajy
深度学习笔记机器学习人工智能
DPODPO(DirectPreferenceOptimization)出自2023年5月的斯坦福大学研究院的论文《DirectPreferenceOptimization:YourLanguageModelisSecretlyaRewardModel》,大概是2023-2024年最广为人知的RLHF的替代对齐方法了。DPO的主要思想是在强化学习的目标函数中建立决策函数与奖励函数之间的关系,以规避
- day59-graph theory-part09-8.30
bbrruunnoo
python开发语言算法
tasksfortoday:1.digkstra堆优化版47.参加科学大会2.bellman_ford算法94.城市间货物运输I---------------------------------------------------------------------------------1.dijkstra堆优化版Thisisanoptimizationforthevanilladijkstra
- python实现蚁群算法
孺子牛 for world
python算法开发语言
蚁群算法(AntColonyOptimization,ACO)是一种模拟蚂蚁觅食行为的启发式算法,常用于解决优化问题,如旅行商问题(TSP)、调度问题等。这里,将提供一个简化的蚁群算法实现,用于解决旅行商问题(TSP)。蚁群算法(ACO)解决TSP问题的基本步骤:初始化:设置蚂蚁数量、信息素挥发系数、信息素增加强度系数等参数,初始化信息素矩阵。构建解:每只蚂蚁随机选择起点,根据信息素浓度和启发式信
- 理解PyTorch版YOLOv5模型构架
LabVIEW_Python
一个深度学习模型,可以拆解为:模型构架(ModelArchitecture):下面详述激活函数(ActivationFunction):YOLOv5在隐藏层中使用了LeakyReLU激活函数,在最后的检测层中使用了Sigmoid激活函数,参考这里优化函数(OptimizationFunction):YOLOv5的默认优化算法是:SGD;可以通过命令行参数更改为Adam损失函数(LossFuncti
- mojo InlinedString实现及详解
启航学途
Mojomojo
inlined_stringImplementsastringthathasasmall-stringoptimizationwhichavoidsheapallocationsforshortstrings.InlinedStringAstringthatperformssmall-stringoptimizationtoavoidheapallocationsforshortstrings.A
- 【HTML】语义化
全宇宙最最帅气的哆啦A梦小怪兽
html前端
根据内容的结构选择合适的标签优点增加代码可读性,结构清晰,便于开发和维护;对机器友好,文字表现力丰富,有利于SEO。SEO(SearchEngineOptimization)是搜索引擎优化,为了让⽤户在搜索和⽹站相关的关键词的时候,可以使⽹站在搜索引擎的排名尽量靠前,从⽽增加流量。方便设备解析(如盲⼈阅读器等),可⽤于智能分析;在没有CSS样式下,⻚⾯也能呈现出很好地内容结构、代码结构。常见的语义
- Introduction to linear optimization 第二章全部课后题答案
心态与习惯
数学优化linearoptimizationintroduction答案课后题
费了好长时间,终于把这本经典理论教材第二章的课后题做完了。大部分都是证明题,很多都是比较有难度的。不少题我参考了网上找到的一些资料的思路,但是有一些题目我觉得这些网上找到的答案也不太好,自己修正完善了下,少部分题目自己独立完成。我把答案放在一个Jupyterbook上,见链接:第二章答案
- 寻参算法之蜘蛛猴优化算法
Network_Engineer
机器学习启发式算法算法深度学习人工智能机器学习
蜘蛛猴优化算法(SpiderMonkeyOptimization,SMO)来历蜘蛛猴优化算法(SpiderMonkeyOptimization,SMO)是受蜘蛛猴觅食行为启发的一种群体智能优化算法。该算法通过模拟蜘蛛猴在森林中觅食的行为,解决复杂的优化问题。自然界中的原型在自然界中,蜘蛛猴在觅食时会通过跳跃和移动寻找食物。蜘蛛猴群体通过信息共享和合作行为,能够高效地找到食物源。SMO通过模拟这一行
- Go 1.22在性能方面有哪些提升?
Toormi
Golanggolang开发语言后端
Go1.22版本在性能方面进行了多项优化,主要包括以下几个方面:1.内存优化CPU性能提升:Go运行时的内存优化使得CPU性能提高了1-3%。这一改进不仅减少了大多数Go程序的内存开销约1%,还提升了整体运行效率[2]。2.Profile-GuidedOptimization(PGO)改进的PGO:Go1.22继续改进了在Go1.21中引入的PGO功能,特别是在接口方法调用的静态调度方面。通过更好
- Go 1.21在性能方面有哪些提升?
Toormi
Golanggolang开发语言后端
Go1.21版本在性能方面取得了多项重要进展,主要体现在以下几个方面:1.Profile-GuidedOptimization(PGO)Go1.21正式推出了PGO功能,使用PGO构建的Go程序性能通常可提升2-7%[2][5]。编译器本身也采用了PGO优化,使得编译速度提高了2-4%[2][3]。2.垃圾回收优化通过调优垃圾回收器,某些应用程序的尾部延迟可减少高达40%[3]。3.其他性能改进在
- 路径优化算法 | 基于蚁群的城市路径优化算法应用及其Matlab实现
算法如诗
路径优化算法(PathOptimization)算法matlab路径优化算法
蚁群算法(AntColonyOptimization,ACO)是一种模拟自然界中蚂蚁觅食行为的优化算法,用于解决如旅行商问题(TSP)等组合优化问题。在蚁群算法中,每只蚂蚁在搜索路径时都会释放信息素,并根据信息素浓度和其他启发式信息来选择下一个节点。随着时间的推移,较短的路径上累积的信息素会更多,从而吸引更多的蚂蚁,最终找到最优路径。在城市路径优化问题中,蚁群算法可以用于找到连接多个城市的最短路径
- 【改进算法】【IHAOAVOA】天鹰优化算法和非洲秃鹫混合优化算法
科研工作站
智能算法算法智能算法天鹰优化算法非洲秃鹫算法
目录1主要内容IHAOAVOA流程图主要创新点2部分代码3程序结果4下载链接1主要内容该程序复现《IHAOAVOA:AnimprovedhybridaquilaoptimizerandAfricanvulturesoptimizationalgorithmforglobaloptimizationproblems》,天鹰优化算法(AO)和非洲秃鹫算法(AVOA)各有优势:AO具有强大的全局勘探能力
- Introduction CMU最优控制16-745超详细学习笔记
我爱科研00
线性代数动态规划
CMU最优控制16-745超详细学习笔记背景跌跌撞撞入坑Optimization-basedMotionPlanning和OptimalControl已经大半年啦,这大半年来迷迷糊糊看了不少相关资料和论文,想借这个机会来整理一下相关的内容,也算是给自己写论文理清一下思路。去年年底做一个移动机械臂移动操作mobilemanipulation课题看了ETHRSL开源框架OCS2(OptimalCont
- 4.SEO
好好学习_fighting
HTMLhtml
SEO经典真题请描述下SEO中的TDK?什么是SEO?SEO由英文SearchEngineOptimization缩写而来,中文意译为“搜索引擎优化”。其实叫做针对搜索引擎优化更容易理解。它是指从自然搜索结果获得网站流量的技术和过程,是在了解搜索引擎自然排名机制的基础上,对网站进行内部及外部的调整优化,改进网站在搜索引擎中的关键词自然排名,获得更多流量,从而达成网站销售及品牌建设的目标。如何进行S
- 10 中科院1区期刊优化算法|基于开普勒优化-卷积-双向长短期记忆网络-注意力时序预测Matlab程序KOA-CNN-BiLSTM-Attention
机器不会学习CSJ
时间序列预测算法网络matlabcnnlstm深度学习
文章目录一、开普勒优化算法二、CNN卷积神经网络三、BiLSTM双向长短期记忆网络四、注意力机制五、KOA-CNN-BiLSTM-Attention时间序列数据预测模型六、获取方式一、开普勒优化算法基于物理学定律的启发,开普勒优化算法(KeplerOptimizationAlgorithm,KOA)是一种元启发式算法,灵感来源于开普勒的行星运动规律。该算法模拟行星在不同时间的位置和速度,每个行星代
- 06基于WOA-CNN-BiLSTM-Attention鲸鱼优化-卷积-双向长短时记忆-注意力机制的数据分类算法
机器不会学习CSJ
数据分类专栏cnn分类深度学习lstmmatlab启发式算法数据分析
基于WOA-CNN-BiLSTM-Attention鲸鱼优化-卷积-双向长短时记忆-注意力机制的数据分类算法鲸鱼智能优化基本原理鲸鱼智能优化算法(WhaleOptimizationAlgorithm,WOA)是一种基于自然界中的鲸鱼群体行为而提出的全局优化算法。该算法由莫扬(SeyedaliMirjalili)于2016年提出,其灵感来源于鲸鱼群体的捕猎行为和社交行为。在WOA算法中,每个解都被看
- 07基于WOA-CNN-BiLSTM-Attention鲸鱼优化-卷积-双向长短时记忆-注意力机制的时间序列预测算法
机器不会学习CSJ
时间序列预测cnn算法人工智能
文章目录鲸鱼优化算法CNN卷积神经网络BiLSTM双向长短期记忆网络Attention注意力机制WOA-CNN-BiLSTM-Attention鲸鱼优化-卷积-双向长短时记忆-注意力机制数据展示代码程序实验结果获取方式鲸鱼优化算法鲸鱼优化算法(WhaleOptimizationAlgorithm,WOA)是一种启发式优化算法,灵感来源于座头鲸的捕食行为。该算法最早由SeyedaliMirjalil
- 基于WOA优化CNN-LSTM-Attention的回归或时序算法,包含多种CNN-LSTM算法进行对比|Matlab
机器不会学习CSJ
算法深度学习
01基于WOA优化CNN-LSTM-Attention的回归或时序算法,包含多种CNN-LSTM算法进行对比|Matlab基础知识:基于WOA-CNN-LSTM-Attention的数据回归算法是一种利用深度学习技术来进行数据回归分析的方法。它结合了WOA(WhaleOptimizationAlgorithm)、CNN(ConvolutionalNeuralNetwork)、LSTM(LongSh
- 【PyTorch Ligntning】快速上手简明指南
何处闻韶
【PyTorchLightning】
目录一、简介二、安装PyTorchLightning三、定义LightningModule3.1SYSTEMVSMODEL3.2FORWARDvsTRAINING_STEP三、配置LightningTrainer四、基本特性4.1Manualvsautomaticoptimization4.1.1自动优化(Automaticoptimization)4.1.1手动优化(Manualoptimiza
- 阅读笔记(TMM2022)Image stitching with manifold optimization
J@u1
传统版图像拼接笔记图像拼接
ZhangL,HuangH.Imagestitchingwithmanifoldoptimization[J].IEEETransactionsonMultimedia,2022.
- 什么是SEO?和SPA与SSR又有什么关系?
才艺のblog
搜索引擎vue.jswebpack
1、什么是SEO?SEO(SearchEngineOptimization):汉译为搜索引擎优化。就是指按照搜索引擎的算法,提升你的文章在搜索引擎中的自然排名,比如百度。那网站在首页有什么好处呢?举个例子,长沙的老王事业很顺利,家庭很幸福,也赚了不少钱,老王和老婆小张一商量,准备把房子重新装修一下,老王的老婆小张也表示想要温馨一点的甜蜜的装修风格于是就百度搜索了一下“长沙装修公司”结果就出来了,看
- 微信小程序分包异步化,分包之间可以互相使用自定义组件
KAGHQ
小程序微信小程序小程序
官网链接转载uni构建的微信小程序中使用1.开启分包在manifest.json文件中对应平台开启分包{"mp-weixin":{/*微信小程序特有相关*/"optimization":{//开启分包"subPackages":true},"appid":"","setting":{"urlCheck":false},"usingComponents":true},}pages同级创建文件夹pac
- 矩阵求逆(JAVA)初等行变换
qiuwanchi
矩阵求逆(JAVA)
package gaodai.matrix;
import gaodai.determinant.DeterminantCalculation;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
/**
* 矩阵求逆(初等行变换)
* @author 邱万迟
*
- JDK timer
antlove
javajdkschedulecodetimer
1.java.util.Timer.schedule(TimerTask task, long delay):多长时间(毫秒)后执行任务
2.java.util.Timer.schedule(TimerTask task, Date time):设定某个时间执行任务
3.java.util.Timer.schedule(TimerTask task, long delay,longperiod
- JVM调优总结 -Xms -Xmx -Xmn -Xss
coder_xpf
jvm应用服务器
堆大小设置JVM 中最大堆大小有三方面限制:相关操作系统的数据模型(32-bt还是64-bit)限制;系统的可用虚拟内存限制;系统的可用物理内存限制。32位系统下,一般限制在1.5G~2G;64为操作系统对内存无限制。我在Windows Server 2003 系统,3.5G物理内存,JDK5.0下测试,最大可设置为1478m。
典型设置:
java -Xmx
- JDBC连接数据库
Array_06
jdbc
package Util;
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.ResultSet;
import java.sql.SQLException;
import java.sql.Statement;
public class JDBCUtil {
//完
- Unsupported major.minor version 51.0(jdk版本错误)
oloz
java
java.lang.UnsupportedClassVersionError: cn/support/cache/CacheType : Unsupported major.minor version 51.0 (unable to load class cn.support.cache.CacheType)
at org.apache.catalina.loader.WebappClassL
- 用多个线程处理1个List集合
362217990
多线程threadlist集合
昨天发了一个提问,启动5个线程将一个List中的内容,然后将5个线程的内容拼接起来,由于时间比较急迫,自己就写了一个Demo,希望对菜鸟有参考意义。。
import java.util.ArrayList;
import java.util.List;
import java.util.concurrent.CountDownLatch;
public c
- JSP简单访问数据库
香水浓
sqlmysqljsp
学习使用javaBean,代码很烂,仅为留个脚印
public class DBHelper {
private String driverName;
private String url;
private String user;
private String password;
private Connection connection;
privat
- Flex4中使用组件添加柱状图、饼状图等图表
AdyZhang
Flex
1.添加一个最简单的柱状图
? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
<?xml version=
"1.0"&n
- Android 5.0 - ProgressBar 进度条无法展示到按钮的前面
aijuans
android
在低于SDK < 21 的版本中,ProgressBar 可以展示到按钮前面,并且为之在按钮的中间,但是切换到android 5.0后进度条ProgressBar 展示顺序变化了,按钮再前面,ProgressBar 在后面了我的xml配置文件如下:
[html]
view plain
copy
<RelativeLa
- 查询汇总的sql
baalwolf
sql
select list.listname, list.createtime,listcount from dream_list as list , (select listid,count(listid) as listcount from dream_list_user group by listid order by count(
- Linux du命令和df命令区别
BigBird2012
linux
1,两者区别
du,disk usage,是通过搜索文件来计算每个文件的大小然后累加,du能看到的文件只是一些当前存在的,没有被删除的。他计算的大小就是当前他认为存在的所有文件大小的累加和。
- AngularJS中的$apply,用还是不用?
bijian1013
JavaScriptAngularJS$apply
在AngularJS开发中,何时应该调用$scope.$apply(),何时不应该调用。下面我们透彻地解释这个问题。
但是首先,让我们把$apply转换成一种简化的形式。
scope.$apply就像一个懒惰的工人。它需要按照命
- [Zookeeper学习笔记十]Zookeeper源代码分析之ClientCnxn数据序列化和反序列化
bit1129
zookeeper
ClientCnxn是Zookeeper客户端和Zookeeper服务器端进行通信和事件通知处理的主要类,它内部包含两个类,1. SendThread 2. EventThread, SendThread负责客户端和服务器端的数据通信,也包括事件信息的传输,EventThread主要在客户端回调注册的Watchers进行通知处理
ClientCnxn构造方法
&
- 【Java命令一】jmap
bit1129
Java命令
jmap命令的用法:
[hadoop@hadoop sbin]$ jmap
Usage:
jmap [option] <pid>
(to connect to running process)
jmap [option] <executable <core>
(to connect to a
- Apache 服务器安全防护及实战
ronin47
此文转自IBM.
Apache 服务简介
Web 服务器也称为 WWW 服务器或 HTTP 服务器 (HTTP Server),它是 Internet 上最常见也是使用最频繁的服务器之一,Web 服务器能够为用户提供网页浏览、论坛访问等等服务。
由于用户在通过 Web 浏览器访问信息资源的过程中,无须再关心一些技术性的细节,而且界面非常友好,因而 Web 在 Internet 上一推出就得到
- unity 3d实例化位置出现布置?
brotherlamp
unity教程unityunity资料unity视频unity自学
问:unity 3d实例化位置出现布置?
答:实例化的同时就可以指定被实例化的物体的位置,即 position
Instantiate (original : Object, position : Vector3, rotation : Quaternion) : Object
这样你不需要再用Transform.Position了,
如果你省略了第二个参数(
- 《重构,改善现有代码的设计》第八章 Duplicate Observed Data
bylijinnan
java重构
import java.awt.Color;
import java.awt.Container;
import java.awt.FlowLayout;
import java.awt.Label;
import java.awt.TextField;
import java.awt.event.FocusAdapter;
import java.awt.event.FocusE
- struts2更改struts.xml配置目录
chiangfai
struts.xml
struts2默认是读取classes目录下的配置文件,要更改配置文件目录,比如放在WEB-INF下,路径应该写成../struts.xml(非/WEB-INF/struts.xml)
web.xml文件修改如下:
<filter>
<filter-name>struts2</filter-name>
<filter-class&g
- redis做缓存时的一点优化
chenchao051
redishadooppipeline
最近集群上有个job,其中需要短时间内频繁访问缓存,大概7亿多次。我这边的缓存是使用redis来做的,问题就来了。
首先,redis中存的是普通kv,没有考虑使用hash等解结构,那么以为着这个job需要访问7亿多次redis,导致效率低,且出现很多redi
- mysql导出数据不输出标题行
daizj
mysql数据导出去掉第一行去掉标题
当想使用数据库中的某些数据,想将其导入到文件中,而想去掉第一行的标题是可以加上-N参数
如通过下面命令导出数据:
mysql -uuserName -ppasswd -hhost -Pport -Ddatabase -e " select * from tableName" > exportResult.txt
结果为:
studentid
- phpexcel导出excel表简单入门示例
dcj3sjt126com
PHPExcelphpexcel
先下载PHPEXCEL类文件,放在class目录下面,然后新建一个index.php文件,内容如下
<?php
error_reporting(E_ALL);
ini_set('display_errors', TRUE);
ini_set('display_startup_errors', TRUE);
if (PHP_SAPI == 'cli')
die('
- 爱情格言
dcj3sjt126com
格言
1) I love you not because of who you are, but because of who I am when I am with you. 我爱你,不是因为你是一个怎样的人,而是因为我喜欢与你在一起时的感觉。 2) No man or woman is worth your tears, and the one who is, won‘t
- 转 Activity 详解——Activity文档翻译
e200702084
androidUIsqlite配置管理网络应用
activity 展现在用户面前的经常是全屏窗口,你也可以将 activity 作为浮动窗口来使用(使用设置了 windowIsFloating 的主题),或者嵌入到其他的 activity (使用 ActivityGroup )中。 当用户离开 activity 时你可以在 onPause() 进行相应的操作 。更重要的是,用户做的任何改变都应该在该点上提交 ( 经常提交到 ContentPro
- win7安装MongoDB服务
geeksun
mongodb
1. 下载MongoDB的windows版本:mongodb-win32-x86_64-2008plus-ssl-3.0.4.zip,Linux版本也在这里下载,下载地址: http://www.mongodb.org/downloads
2. 解压MongoDB在D:\server\mongodb, 在D:\server\mongodb下创建d
- Javascript魔法方法:__defineGetter__,__defineSetter__
hongtoushizi
js
转载自: http://www.blackglory.me/javascript-magic-method-definegetter-definesetter/
在javascript的类中,可以用defineGetter和defineSetter_控制成员变量的Get和Set行为
例如,在一个图书类中,我们自动为Book加上书名符号:
function Book(name){
- 错误的日期格式可能导致走nginx proxy cache时不能进行304响应
jinnianshilongnian
cache
昨天在整合某些系统的nginx配置时,出现了当使用nginx cache时无法返回304响应的情况,出问题的响应头: Content-Type:text/html; charset=gb2312 Date:Mon, 05 Jan 2015 01:58:05 GMT Expires:Mon , 05 Jan 15 02:03:00 GMT Last-Modified:Mon, 05
- 数据源架构模式之行数据入口
home198979
PHP架构行数据入口
注:看不懂的请勿踩,此文章非针对java,java爱好者可直接略过。
一、概念
行数据入口(Row Data Gateway):充当数据源中单条记录入口的对象,每行一个实例。
二、简单实现行数据入口
为了方便理解,还是先简单实现:
<?php
/**
* 行数据入口类
*/
class OrderGateway {
/*定义元数
- Linux各个目录的作用及内容
pda158
linux脚本
1)根目录“/” 根目录位于目录结构的最顶层,用斜线(/)表示,类似于
Windows
操作系统的“C:\“,包含Fedora操作系统中所有的目录和文件。 2)/bin /bin 目录又称为二进制目录,包含了那些供系统管理员和普通用户使用的重要
linux命令的二进制映像。该目录存放的内容包括各种可执行文件,还有某些可执行文件的符号连接。常用的命令有:cp、d
- ubuntu12.04上编译openjdk7
ol_beta
HotSpotjvmjdkOpenJDK
获取源码
从openjdk代码仓库获取(比较慢)
安装mercurial Mercurial是一个版本管理工具。 sudo apt-get install mercurial
将以下内容添加到$HOME/.hgrc文件中,如果没有则自己创建一个: [extensions] forest=/home/lichengwu/hgforest-crew/forest.py fe
- 将数据库字段转换成设计文档所需的字段
vipbooks
设计模式工作正则表达式
哈哈,出差这么久终于回来了,回家的感觉真好!
PowerDesigner的物理数据库一出来,设计文档中要改的字段就多得不计其数,如果要把PowerDesigner中的字段一个个Copy到设计文档中,那将会是一件非常痛苦的事情。
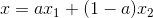
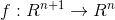 .
. ![x^*=[\vec{x},t]\in R^{n+1}, f(x^*)=\{\vec{x}/t|t>0\}.](http://img.e-com-net.com/image/info8/7081f406bb984883903f2d138538ab17.gif)
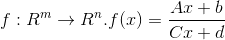 ,with the denominator >0.
,with the denominator >0.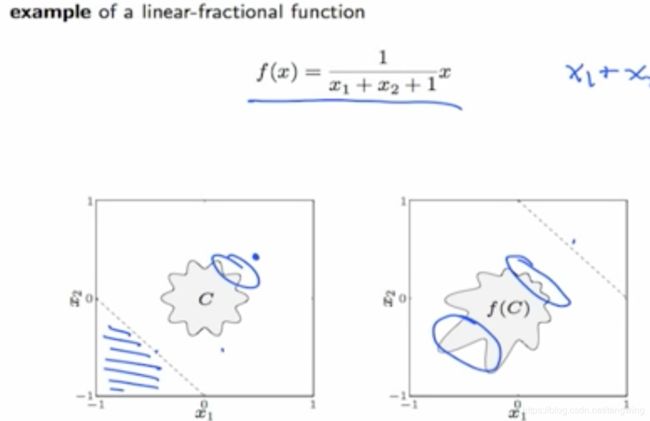 can be seen as a streching of vision, or the projection of a 3d object onto a camera. x=[x1,x2]. If the object is convex then the result is convex too.
can be seen as a streching of vision, or the projection of a 3d object onto a camera. x=[x1,x2]. If the object is convex then the result is convex too.![]() , reads "x less than y with respect to proper cone K". Remember K somehow define a 'positive' space, consider an orthant. The coordinates y-x must still in the same orthant.
, reads "x less than y with respect to proper cone K". Remember K somehow define a 'positive' space, consider an orthant. The coordinates y-x must still in the same orthant.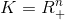 , x
, x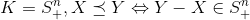 ,(w.r.t positive semidefinite)
,(w.r.t positive semidefinite) , but the latter defines also a "linear ordering", while the former doesn't, where comes the difference between Minimum (less than anyone else) and Minimal(less than anyone else that are comparable).
, but the latter defines also a "linear ordering", while the former doesn't, where comes the difference between Minimum (less than anyone else) and Minimal(less than anyone else that are comparable).