算法——回溯法(子集、全排列、皇后问题)
参考:http://www.cnblogs.com/wuyuegb2312/p/3273337.html#intro
参考:《算法竞赛入门经典》 P120
1、定义
回溯算法也叫试探法,它是一种系统地搜索问题的解的方法。
回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。
回溯算法解决问题的一般步骤为:
1、定义一个解空间,它包含问题的解。
2、利用适于搜索的方法组织解空间。
3、利用深度优先法搜索解空间。
4、利用限界函数避免移动到不可能产生解的子空间。
问题的解空间通常是在搜索问题的解的过程中动态产生的,这是回溯算法的一个重要特性。
确定了解空间的组织结构后,回溯法就从开始结点(根结点)出发,以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点,同时也成为当前的扩展结点。在当前的扩展结点处,搜索向纵深方向移至一个新结点。这个新结点就成为一个新的活结点,并成为当前扩展结点。如果在当前的扩展结点处不能再向纵深方向移动,则当前扩展结点就成为死结点。此时,应往回移动(回溯)至最近的一个活结点处,并使这个活结点成为当前的扩展结点。
回溯法即以这种工作方式递归地在解空间中搜索,直至找到所要求的解或解空间中已没有活结点时为止。
/*
对于其中的函数和变量,解释如下:
a[]表示当前获得的部分解;
k表示搜索深度;
input表示用于传递的更多的参数;
is_a_solution(a,k,input)判断当前的部分解向量a[1...k]是否是一个符合条件的解
construct_candidates(a,k,input,c,ncandidates)根据目前状态,构造这一步可能的选择,存入c[]数组,其长度存入ncandidates
process_solution(a,k,input)对于符合条件的解进行处理,通常是输出、计数等
make_move(a,k,input)和unmake_move(a,k,input)前者将采取的选择更新到原始数据结构上,后者把这一行为撤销。
*/
bool finished = FALSE; /* 是否获得全部解? */
backtrack(int a[], int k, data input)
{
int c[MAXCANDIDATES]; /*这次搜索的候选 */
int ncandidates; /* 候选数目 */
int i; /* counter */
if (is_a_solution(a,k,input))
process_solution(a,k,input);
else
{
k = k+1;
construct_candidates(a,k,input,c,&ncandidates);
for (i=0; i
{
a[k] = c[i];
make_move(a,k,input);
backtrack(a,k,input);
unmake_move(a,k,input);
if (finished)
return; /* 如果符合终止条件就提前退出 */
}
}
} 2、给出数组,求全排列
《算法竞赛入门经典》 P116
给出一个数组,将其按字典序形成全排列。
例如给出:a[] = {3, 1, 2};
我们可以先将其排序,a[] = {1,2,3};然后再全排列。
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2 这里有对全排列的一个综合的概括:http://blog.csdn.net/morewindows/article/details/7370155/
1.全排列就是从第一个数字起每个数分别与它后面的数字交换。
2.去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。
3.全排列的非递归就是由后向前找替换数和替换点,然后由后向前找第一个比替换数大的数与替换数交换,最后颠倒替换点后的所有数据。
1:递归方法
分别将每个位置交换到最前面位,之后全排列剩下的位。
【例】递归全排列 1 2 3 4 5
1,for循环将每个位置的数据交换到第一位
swap(1,1~5)
2,按相同的方式全排列剩余的位
/// 递归方式生成全排列的方法
//fromIndex:全排列的起始位置
//endIndex:全排列的终止位置
void PermutationList(int fromIndex, int endIndex)
{
if (fromIndex > endIndex)
Output(); //打印当前排列
else
{
for (int index = fromIndex; index <= endIndex; ++index)
{
// 此处排序主要是为了生成字典序全排列,否则递归会打乱字典序
Sort(fromIndex, endIndex);
Swap(fromIndex, index);
PermutationList(fromIndex + 1, endIndex);
Swap(fromIndex, index);
}
}
}添加排序函数
int comp2(const void*a,const void*b)
{
return *(int*)a - *(int*)b;
}
int list[] = {4, 3, 1, 2, 5};
qsort(list,5,sizeof(int),comp2);2、非递归方法(字典序法):
这种算法被用在了C++的STL库中。
对给定的字符集中的字符规定了一个先后关系,在此基础上规定两个全排列的先后是从左到右逐个比较对应的字符的先后。
[例]字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是:
123,132,213,231,312,321
※ 一个全排列可看做一个字符串,字符串可有前缀、后缀。
生成给定全排列的下一个排列.所谓一个的下一个就是这一个与下一个之间没有其他的。这就要求这一个与下一个有尽可能长的共同前缀,也即变化限制在尽可能短的后缀上。
[例]839647521是1–9的排列。1—9的排列最前面的是123456789,最后面的987654321,从右向左扫描若都是增的,就到了987654321,也就没有下一个了。否则找出第一次出现下降的位置。
【例】 一般而言,设P是[1,n]的一个全排列。
P=P1P2…Pn=P1P2…Pj-1PjPj+1…Pk-1PkPk+1…Pn
find: j=max{i|Pi
void PermutationList(int *list, int n)
{
int i,j,k,diff;
int all_increase = 0;
qsort(list,n,sizeof(int),comp2);
for(i=0;iprintf("%d ",list[i]);
printf("\n");
while(1)
{
//从尾部往前找第一个P(i-1) < P(i)的位置
for(i=n-1; i>0; i--)
{
if(list[i-1] < list[i])
break;
}
if(i == 0) //从尾部开始全部为增序时,全排列结束
break;
//从i位置往后找到最后一个大于i-1位置的数
//即其差最小
diff = list[i] - list[i-1];
k = i;
for(j=i; jif(list[j] > list[i-1] && diff > list[j]-list[i-1])
{
diff = list[j] - list[i-1];
k = j;
}
}
//交换位置i-1和k的值
swap2(list+i-1,list+k);
//倒序i后的数
for(j=i,k=n-1; j< k; j++,k--)
{
swap2(list+j,list+k);
}
for(i=0;iprintf("%d ",list[i]);
printf("\n");
}
} 参考:http://www.cnblogs.com/pmars/archive/2013/12/04/3458289.html
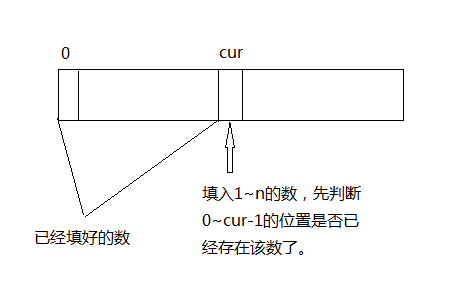
3、给出n,求1~n的全排列
《算法竞赛入门经典》 P116
输入一个整数,例如3,生成1、2、3的全排列。
输出为:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1 void print_permutation(int *a, int n, int cur)
{
int i,j;
if(cur == n)
{
for(i=0;iprintf("%d ",a[i]);
printf("\n");
}
else
{
int exist = 0;
for(i=1;i<=n;i++) //尝试在a[cur]中填入1~n的数
{
exist = 0;
for(j=0;jif(i == a[j])
exist = 1;
}
if(!exist)
{
a[cur] = i;
print_permutation(a,n,cur+1);
}
}
}
} 4、子集生成
《算法竞赛入门经典》 P120
给定一个n,枚举0~n的所有子集。
例如:n=4,枚举0,1,2,3,4的子集。
子集:
0
0 1
0 1 2
0 1 2 3
0 1 3
0 2
0 2 3
0 3
1
1 2
1 2 3
1 3
2
2 3
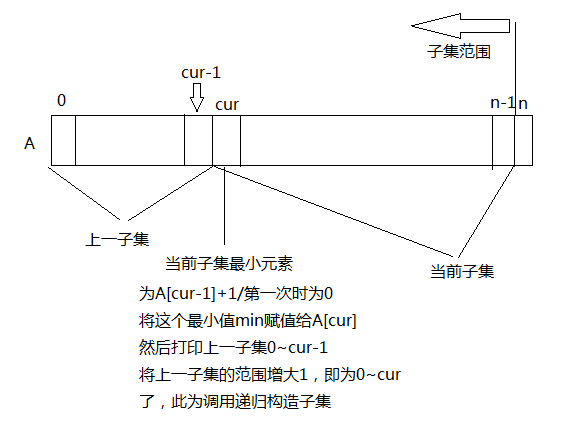
3 1、增量构造法
/*递归输出0~n所有子集,其中cur为当前下标,cur-1表示上一层最后一个元素下标,初始值0*/
void print_subset(int *a, int n, int cur)
{
int i,min;
//for(i=0;i
for(i=0;i<=cur-1;i++) //输出上一层子集0~cur-1的位置。
printf("%d ",a[i]);
printf("\n");
//找到当前子集首个值,因为按字典顺序输出,所以每次找到最小的元素
min = cur ? a[cur-1]+1 : 0; //每次获得当前集的最小元素,要么是0,要么是上一层最后一个元素+1
/*************************************************************/
/* 以上为每次递归都会执行的两个操作,1、输出上一子集 2、找到当前子集的首个值 */
for(i=min;i//循环处理:当前集的最小元素min~n-1的元素
{
a[cur] = i; //将当前子集的最小值,也就是第一个元素给a[cur]
print_subset(a,n,cur+1); //递归,扩大当前子集的范围cur+1,在递归中输出递归前的前一个子集的集合
}
}2、二进制法
/*输出子集s*/
/*
* 当s=151=1001 0111 时,输出为0 1 2 4 7(子集)
* n表示为总集合
* 当n=8
* s= 0000 0001 时,输出为0
*/
void print_subsetn(int n, int s)
{
int i;
for(i=0; iif(s & (1<//如果s中的i位为1
printf("%d ",i); //打印s中位数为1的位数号i
}
printf("\n");
}
/*输出0~n所有子集*/
void print_subset(int n)
{
int i;
for(i=0; i<(1<//i表示子集,0~2^n-1从空集到全集的范围,全集{0,1,...,n-1}二进制为n个1,即2^n-1
print_subsetn(n,i);
}
/*
* 当n=2时,二进制法的二进制长度就为2
* 那么空集=0 全集=3
* i=0=00 => 输出空集
* i=1=01 => 输出{0}
* i=2=10 => 输出{1}
* i=3=11 => 输出{0,1}
*/ 5、从n个数中选m个数的组合
1、n个数存放在数组b中。
【思路】
从后往前选,先确定一个数,例如在b[4] = {1,2,3,4}中,先确定4,然后再在剩下的1,2,3中选m-1个数,这是一个递归的形式。
例如:在1 2 3 4 5中选3个数
先确定5,然后在1 2 3 4 中选2个数
5完成后,确定4,再在1 2 3 中选2个数,如此递归。
//在b数组中选m个数
//n: b数组的个数 j为全局数组a的指针。
void choose(int *b,int n, int m, int j)
{
int i,k;
if(m == 0)
{
for(i=0;iprintf("%d",a[i]);
printf("\n");
return;
}
for(i=n; i>0;i--) //从后往前选
{
a[j] = b[i-1];
//choose(b,n-1,m-1,j+1); //在1~n-1中选取m-1个数
choose(b,i-1,m-1,j+1); //将n-1改为i-1解决了出现重复数字的情况,例如:43 42 41 33 32 31 22 21 11
}
} 2、从1~n中选m个数的组合,不利用数组b
//在1~n中选m个数
void choose(int n, int m, int j)
{
int i,k;
if(m == 0)
{
for(i=0;iprintf("%d",a[i]);
printf("\n");
return;
}
for(i=n; i>0;i--) //从后往前选
{
a[j] = i;
choose(i-1,m-1,j+1);
}
} 参考: http://blog.csdn.net/wumuzi520/article/details/8087501
6、在1-n中选取m个字符进行全排列
int vis[11];
void chos(int n, int m, int j)
{
int i;
//if(m == 0)
if(m == j)
{
for(i=0;iprintf("%d ",a[i]);
printf("\n");
}
for(i=1; i<=n; i++)
{
if(!vis[i])
{
a[j] = i;
vis[i] = 1;
//chos(n-1,m-1,j+1);
chos(n,m,j+1); //因为有vis数组判断某个数是否已经加入到输出的集合了,所有不需要n-1
vis[i] = 0;
}
}
return;
} ACM:http://acm.nyist.net/JudgeOnline/problem.php?pid=19
八皇后问题
《算法竞赛入门经典》 P125
在8* 8的棋盘上摆放8个皇后,使其不能互相攻击,即任意的两个皇后不能处在同意行,同一列,或同一斜线上(不能在一条左斜线上,当然也不能在一条右斜线上)。可以把八皇后问题拓展为n皇后问题,即在n*n的棋盘上摆放n个皇后,使其任意两个皇后都不能处于同一行、同一列或同一斜线上。
//一个N皇后问题的处理
void Queen(int j, int (*Q)[N])
{
if(j == N) //j从0开始一步一步往右边逼近,当到达N时,前面的都已放好。
{
//得到一个解,输出数组Q
return;
}
//对j列的每一行进行探测,看是否能够放置皇后
for(int i=0; i//i表示行,j表示列
{
if(isCorrect(i,j,Q)) //如果可以在i行,j列中放置皇后(判断同行同列斜线上是否已有皇后)
{
Q[i][j] = 1; //放置皇后
Queen(j+1,Q); //深度递归,继续放下一列
Q[i][j] = 0; //回溯
}
}
} /*
* n皇后处理
* cur表示行,col[cur]表示第cur行皇后的列编号,tot表示解的个数
* 算法的过程:起始列按0~n-1,每次按行放置(cur初始值为0),循环寻找从第0列~第n-1列能放置皇后的位置,找到后进行下一
* 行的放置。
* 当所有行都放置成功后,解的个数加一。
*/
int tot = 0;
int col[50];
void search(int n, int cur)
{
int i,j,ok;
if(cur == n) //行数达到最大
{
tot++;
}
else
{
for(i=0; i//列
{
ok = 1; //放置标志位
col[cur] = i; //尝试将第cur行的皇后放在第i列
for(j=0; j//从第0行开始到cur-1行,检查是否和前面的皇后有冲突
{
if(col[cur] == col[j] || //在同一列
cur-col[cur] == j-col[j] || //主对角线
cur+col[cur] == j+col[j] ) //副对角线
{
ok = 0;
break; //当前i列存在冲突,换下一列
}
}
if(ok) //如果当前行cur找到放置点后,继续下一行的放置
{
search(n,cur+1);
}
}
}
}
int main()
{
int n;
scanf("%d",&n);
search(n,0);
printf("%d\n",tot);
} 八皇后问题就是回溯算法的典型,第一步按照顺序放一个皇后,然后第二步符合要求放第2个皇后,如果没有位置符合要求,那么就要改变第一个皇后的位置,重新放第2个皇后的位置,直到找到符合条件的位置就可以了。
int vis[3][]; //记录当前尝试的皇后所在的列|正斜线|负斜线是否已有其他皇后
void search_ex(int n, int cur)
{
int i,j,ok;
if(cur == n) //行数达到最大
{
tot++;
}
else
{
for(i=0; i//列
{
if(!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n]) //可放置
{
col[cur] = i; //尝试将第cur行的皇后放在第i列
vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1;
search_ex(n,cur+1);
vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0;
}
}
}
}