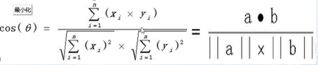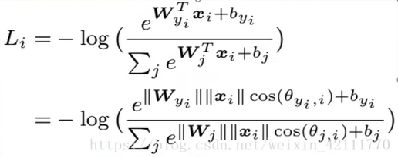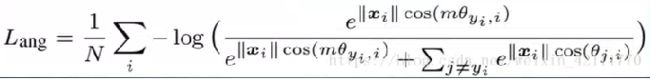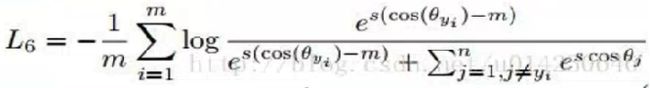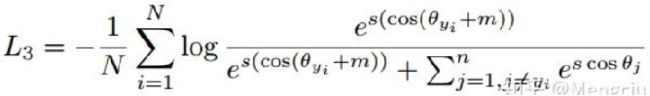人脸识别损失函数
一、人脸识别
人脸识别:基于脸部特征信息进行身份识别的一种生物识别技术。
人脸识别属于分类问题,每个人的脸都是一个类别,而他/她的所有图片都是这个类的样本。
如下图:
胡歌的脸为一个类别,所有图片为这个类别的样本。 刘亦菲的脸为另一个类别。

人脸识别的步骤:
1,人脸检测:使用MTCNN等目标检测算法,检测到图片中是否存在人脸,若存在人脸则检测出人脸的位置区域,然后框出。
2,特征提取:将检测到的人脸框输入到特征提取网络中进行特征提取,返回的是一些特征数据。
3,特征对比:将提取到的特征数据,上传到注册库或数据库中和已经存储的数据标签,进行数据对比,找到相似度最大的数据,输出人脸、姓名以及其他信息。
人脸识别的难点:
1、每个人脸分类界限不明显:因为每个人都有眉毛,眼睛,鼻子,嘴巴等特征。
2、人脸的相似度很高,有时人也难以区分:就像双胞胎、网红脸等。
3、如何解决人脸特征分类困难的问题:
网络模型:ResNet(残差神经网络)、DSCNet(深度可分离卷积神经网络)、DenseNet(稠密神经网络)等
损失函数:SoftmaxLoss,CenterLoss(中心损失函数),ArcFaceLoss(ArcSoftmaxLoss)等
如何实现人脸特征分类,最重要的还是损失函数,下面我们来了解上面的损失函数。
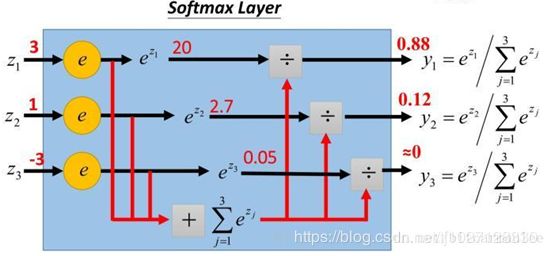
二、Softmax激活函数
要想了解SoftmaxLoss损失函数就要先从Softmax激活函数开始。
理解Softmax激活函数:
将所有类别数据zi(常数)输入Softmax,他会将每个类别数据分别除以所有类别数据得到该类别的占比yi,这个输出是一个离散型的概率分布,表示是第i个类的可能性。
公式:
公式1:Vi表示一个人脸/类的特征数据,ΣVj表示所有人脸/类的特征数据的和,Si表示表示这个人脸/类是第i个人脸/类的概率
公式2:W表示权重,T表示转置,Xi表示样本,b表示偏置,和公式1的意义相同
性质:1、因Softmax输出是一个离散型的概率分布所以没有图像。
2、值域:(0, 1);ΣSj=1所有输出结果的和为1。
三、SoftmaxLoss损失函数
SoftmaxLoss公式理解:
公式: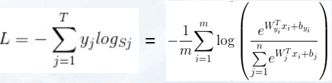
从公式中可以看出,SoftmaxLoss损失函数只是在Softmax的基础上加了个Log,求均值然后再加了个负号
由于yi为独热编码(one_hot)0和1,所以公式简化为:![]()
图像: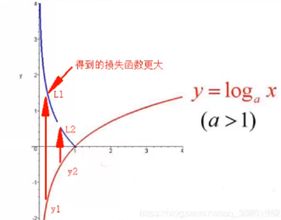
因为Softmax值域为(0, 1)之间,加了log变成单调递增函数,再加负号变成单调递减函数,这样就使初始的损失更大,才有足够的空间训练,而随着训练的增加,损失越来越小。
SoftmaxLoss与CELoss(交叉熵损失函数)的区别:
CELoss公式: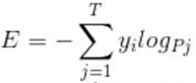
当Pj为Softmax激活函数输出的(0, 1)概率时与SoftmaxLoss是等价的。
SoftmaxLoss性质:定义域(0, 1), 值域(0, +∞)
Loss越小,Softmax输出的概率值越大,训练效果越好。
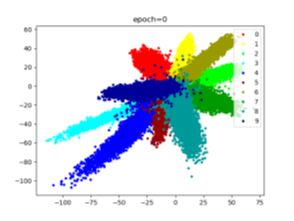
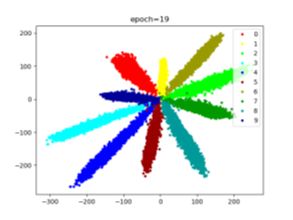
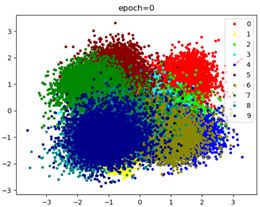
MNIST数据集使用SoftmaxLoss分类效果:
Adam优化器:
SGD优化器(lr=0.01, momentum=0.9):
SoftmaxLoss的缺点:分类分的不够开(中间部分)
类分开的方法:减小类内距(CenterLoss)
增大类间距(ArcFaceLoss)
四、CenterLoss(中心损失函数)
公式: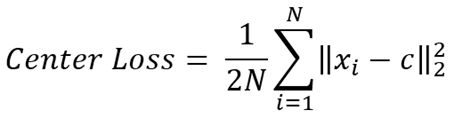
xi为样本,c为中心点,N为每批次的样本个数,从公式中可以看出是样本到中心点距离的平方和再求均值,2是为了方便求导
降低损失就是减少样本点和中心点的距离,减小类内距
导数公式:
α代表的是学习率,一般设置为0.5
SoftmaxLoss只能减小类内距,并不能分类,所以需要搭配SoftmaxLoss使用(辅助作用)
SoftmaxLoss+CenterLoss:
公式: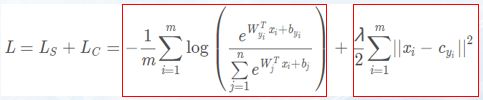
Ls为SoftmaxLoss,Lc为CenterLoss,SoftmaxLoss只能分类,不能减少或增大类内或类间距离,因为CenterLoss减小类内距,相对而言SoftmaxLoss增大类间距。
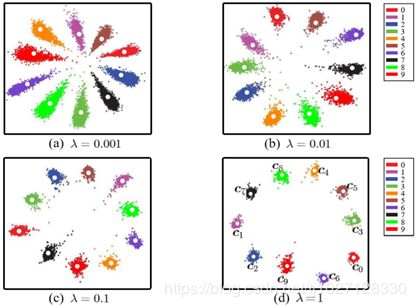
λ为两个损失的权重参数(超参数控制比例)
从上图中可以看出,λ越大越侧重于CenterLoss损失函数,类内距的效果越好,我们测试MNIST数据集使用λ=2
使SoftmaxLoss和CenterLoss各占一半
SoftmaxLoss和CenterLoss的网络架构: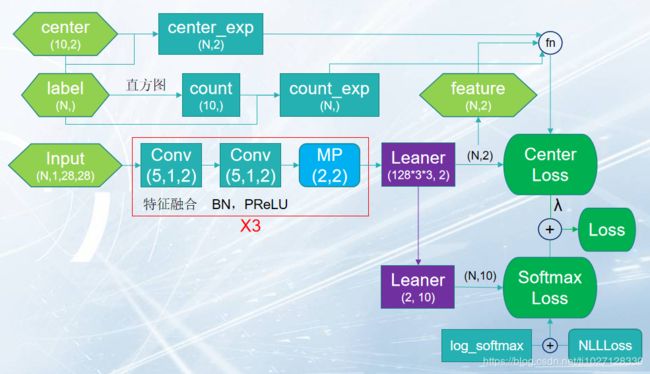
这里我们测试的是MNIST数据集,有10类别所以中心点center有10个(2表示中心点的位置x,y为了可视化)
SoftmaxLoss为-mean(log(Softmax)),NLLLoss为求均值加负号,所以SoftmaxLoss=log_softmax+NLLLoss
CenterLoss可以写成方法也可以写成网络,因为网络可以学习center中心点的位置分类更快
代码:
centerLoss方法:
def center_loss(feature, label, lambdas):
center = nn.Parameter(torch.randn(label.shape[0], feature.shape[1]), requires_grad=True).cuda() # (100, 2)
center_exp = center.index_select(dim=0, index=label.long()) # (100, 2)
count = torch.histc(label, bins=int(max(label).item() + 1), min=int(min(label).item()), max=int(max(label).item())) # (10,)
count_exp = count.index_select(dim=0, index=label.long()) # (100,)
loss = lambdas/2 * torch.mean(torch.div(torch.sum(torch.pow(feature - center_exp, 2), dim=1), count_exp))
return lossCenterLoss网络:
import torch
import torch.nn as nn
class CLNet(nn.Module):
def __init__(self):
super().__init__()
self.center = nn.Parameter(torch.randn(10, 2), requires_grad=True)
def forward(self, feature, label, lambdas=2):
center_exp = self.center.index_select(dim=0, index=label.long())
count = torch.histc(label, bins=int(max(label).item() + 1), min=int(min(label).item()), max=int(max(label).item()))
count_exp = count.index_select(dim=0, index=label.long())
loss = lambdas / 2 * torch.mean(torch.div(torch.sum(torch.pow(feature - center_exp, 2), dim=1), count_exp))
return loss
if __name__ == "__main__":
data = torch.tensor([[1, 2], [3, 4], [5, 6], [7, 8], [9, 8]], dtype=torch.float32)
target = torch.tensor([0, 1, 0, 1, 1], dtype=torch.float32)
center_loss = CLNet()
print(center_loss(data, target, 2))
主网络:
import torch
import torch.nn as nn
class Net(nn.Module):
def __init__(self):
super().__init__()
self.layer = nn.Sequential(
nn.Conv2d(1, 32, 5, 1, 2), # (32,28,28) (28-5+2*2)/1+1=28
nn.BatchNorm2d(32),
nn.PReLU(),
nn.Conv2d(32, 32, 5, 1, 2), # (32,28,28)
nn.BatchNorm2d(32),
nn.PReLU(),
nn.MaxPool2d(2, 2), # (32,14,14) (28-2+2*0)/2+1=14
nn.Conv2d(32, 64, 5, 1, 2), # (64,14,14)
nn.BatchNorm2d(64),
nn.PReLU(),
nn.Conv2d(64, 64, 5, 1, 2), # (64,14,14)
nn.BatchNorm2d(64),
nn.PReLU(),
nn.MaxPool2d(2, 2), # (64,7,7)
nn.Conv2d(64, 128, 5, 1, 2), # (128,7,7)
nn.BatchNorm2d(128),
nn.PReLU(),
nn.Conv2d(128, 128, 5, 1, 2), # (128,7,7)
nn.BatchNorm2d(128),
nn.PReLU(),
nn.MaxPool2d(2, 2), # (128,3,3)
)
self.feature = nn.Linear(128*3*3, 2)
self.output = nn.Linear(2, 10)
def forward(self, x):
x = torch.reshape(self.layer(x), (-1, 128*3*3))
feature = self.feature(x)
output = torch.log_softmax(self.output(feature), dim=1)
return feature, output
if __name__ == "__main__":
data = torch.randn(1, 1, 28, 28)
net = Net()
print(net(data))
训练:
import torch
from my_net import Net
from center_loss_net import CLNet
import torch.nn as nn
from torchvision import datasets, transforms
import os
from tools.utils import visualize
class Trainer:
def __init__(self):
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.s_net = Net().to(self.device)
self.c_net = CLNet().to(self.device)
self.s_save_path = "models/s_net.pth"
self.c_save_path = "models/c_net_pth"
self.s_loss_fn = nn.NLLLoss()
self.s_optimizer = torch.optim.SGD(self.s_net.parameters(), lr=0.001, momentum=0.9)
self.c_optimizer = torch.optim.SGD(self.c_net.parameters(), lr=0.5)
self.scheduler = torch.optim.lr_scheduler.ExponentialLR(self.s_optimizer, gamma=0.95)
self.mean, self.std = self.mean_std()
self.dataLoader = self.data_loader()
def mean_std(self):
sets = datasets.MNIST("datasets/", train=True, download=True, transform=transforms.ToTensor())
loader = torch.utils.data.DataLoader(sets, batch_size=len(sets), shuffle=True)
data = next(iter(loader))[0]
mean = round(torch.mean(data, dim=(0, 2, 3)).item(), 3)
std = round(torch.std(data, dim=(0, 2, 3)).item(), 3)
return mean, std
def data_loader(self):
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((self.mean,), (self.std,))
])
dataSet = datasets.MNIST("datasets/", train=True, download=True, transform=transform)
dataLoader = torch.utils.data.DataLoader(dataSet, batch_size=100, shuffle=True, num_workers=4)
return dataLoader
def train_test(self):
if os.path.exists(self.s_save_path) and os.path.exists(self.c_save_path):
self.s_net.load_state_dict(torch.load(self.s_save_path))
self.c_net.load_state_dict(torch.load(self.c_save_path))
else:
"No models!"
epoch = 0
while True:
feature_loader = []
label_loader = []
for i, (x, y) in enumerate(self.dataLoader):
x = x.to(self.device)
y = y.to(self.device)
feature, out = self.s_net(x)
s_loss = self.s_loss_fn(out, y)
y = y.float()
c_loss = self.c_net(feature, y, 2)
loss = s_loss + c_loss
self.s_optimizer.zero_grad()
self.c_optimizer.zero_grad()
loss.backward()
self.s_optimizer.step()
self.c_optimizer.step()
feature_loader.append(feature)
label_loader.append(y)
if i % 100 == 0:
print("epoch:{}, i:{}, loss:{:.3f}, softmax_loss:{:.3f}, center_loss:{:.3f}".format(epoch, i, loss.item(), s_loss.item(), c_loss.item()))
features = torch.cat(feature_loader, dim=0)
labels = torch.cat(label_loader, dim=0)
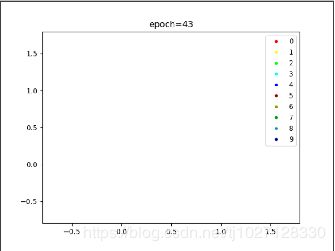
visualize(features.cpu().data.numpy(), labels.cpu().data.numpy(), epoch)
torch.save(self.s_net.state_dict(), self.s_save_path)
torch.save(self.c_net.state_dict(), self.c_save_path)
self.scheduler.step(None)
epoch += 1
if epoch == 50:
break
if __name__ == "__main__":
trainer = Trainer()
trainer.train_test()
可视化:
import matplotlib.pyplot as plt
def visualize(features, labels, epoch):
colors = ["#ff0000", "#ffff00", "#00ff00", "#00ffff", "#0000ff",
"#990000", "#999900", "#009900", "#009999", "#000099"]
plt.clf()
for i in range(10):
plt.plot(features[labels == i, 0], features[labels == i, 1], ".", c=colors[i])
plt.legend(["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"], loc="upper right")
plt.title("epoch=%d" % epoch)
plt.savefig("images/epoch%d=" % epoch)
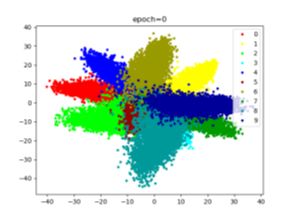
效果:
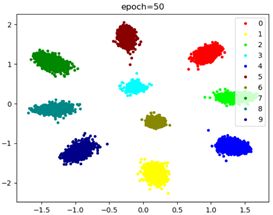
centerLoss方法单优化器效果:
CenterLoss写成网络使用双优化器效果:
CenterLoss缺点:
1、类别较多时对硬件要求较高:因为类别较多时,每个类都要学习中心点,和样本到中心点的距离,计算量大所以对硬件要求较高
2、L2范数离群点对Loss影响较大:因为CenterLoss是求的L2范数(距离)的平方的均值,离群点不易回归,所以导致Loss下降的很慢但是离群点回归的也慢。
3、类内距太大:因为人脸识别每个人的脸随着光照、年龄、形态、化妆等因素使类内距较大,如果想要损失降低,需要大量的训练,容易过拟合。
4、只适合同类样本差别不大的数据:人脸差别相对较小,像狗、猫等有很多品种,不同品种之间差别很大。
五、ArcFaceLoss
向量相关性:两个向量之间的差异
如何表示向量相关性:
1、余弦相似度:
空间中两向量夹角间的余弦值。
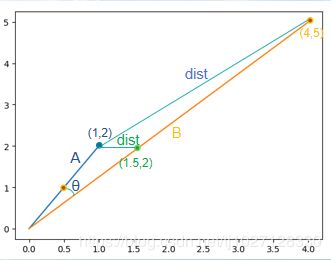
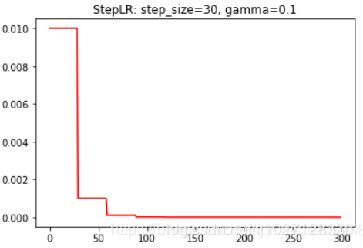
正相关:0°≤θ<90° 0 不相关:θ=90° cosθ=0 负相关:90°<θ≤180° -1≤cosθ<0 空间中两向量终点之间的距离。 cosθ为两向量的余弦相似度 dist(A,B)为两向量的欧式距离 余弦相似度通过角度衡量,欧式距离通过距离衡量 欧式距离大,夹角θ不一定大 标准化后的两个向量(L2范数模长都为1),他们的欧氏距离的平方与余弦距离成正比。 余弦相似度与L2范数标准化的欧氏距离等价。 向量A'和向量B'分别为向量A和向量B的L2范数标准化后的向量 L2范数标准化:将两向量压缩到x = [-1, 1],y = [-1, 1]的区间中 A = (1, 2) B = (4, 5) 均值=3 A' = (-2, -1) B' = (1, 2) 再归一化 A' = (-1, -0.5) B' = (0.5, 1) 这时发现A'B'的欧式距离dist'很大,所以与cosθ等价 由SoftmaxLoss公式W*x变化为余弦相似度W*x*cosθ W二范数归一化 ||W||=1,偏置b=0 m为角度乘积系数(m>1的整数) A-SoftmaxLoss是通过增加m来增大向量角度。 AM-SoftmaxLoss通过减少相似度系数m(增大余弦距离)来增大向量之间的距离。 AM-SoftmaxLoss对x进行二范数归一化 ||x||=1,乘以缩放系数s=||W|| * ||x|| 因使用的倍角公式,不方便反向求导。 A_SoftmaxLoss是通过角度衡量,AM_SoftmaxLoss是通过余弦相似度(余弦距离)衡量 因增大角度比减小相似度距离对分类影响更加直接 m为弧度,1弧度=180°/3.14...≈53.7° ArcFaceLoss网络: 主网络: 训练: 可视化: 训练CenterLoss时会经常出现梯度爆炸的情况 如图: 可以使用lr_scheduler 阶梯衰减:StepLR(optimizer, step_size=10, gamma=0.6) step_size表示epoch轮次,每step_size更新一次lr,gamma为更新比例,更新公式为:lr=lr*gamma 指数衰减:ExponentialLR(optimizer, gamma=0.95) gamma为更新的比率,每轮结束都会更新,更新公式:lr=lr * gamma^epoch2、欧氏距离:
3、二维空间图示:
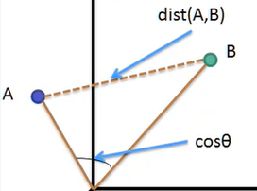
4、余弦相似度和欧式距离的区别:
5、余弦相似度和欧氏距离的等价性:
A_SoftmaxLoss
AM_SoftmaxLoss
A_SoftmaxLoss与AM_SoftmaxLoss的区别:
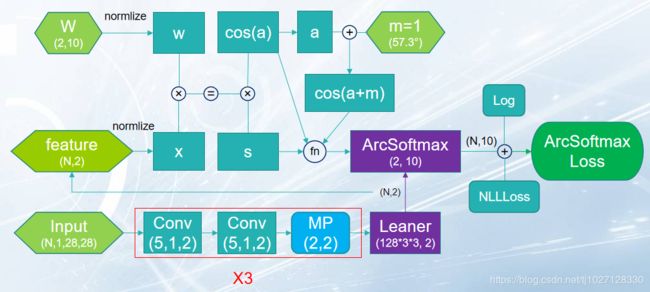
ArcSoftmaxLoss(ArcFaceLoss):
ArcFaceLoss网络架构:
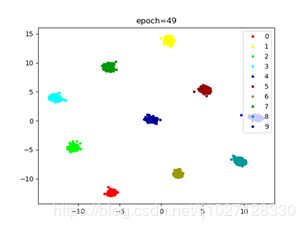
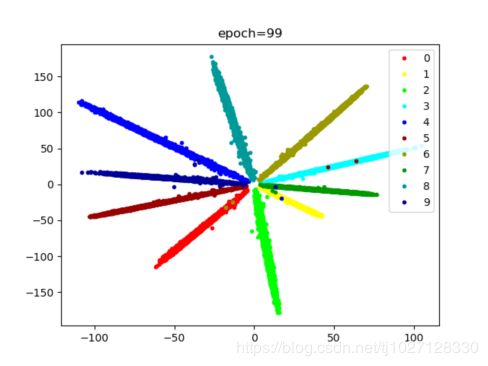
MNIST数据集ArcFaceLoss的分类效果:
代码:
import torch
import torch.nn as nn
class ArcNet(nn.Module):
def __init__(self, feature_dim=2, cls_dim=10):
super().__init__()
self.W = nn.Parameter(torch.randn(feature_dim, cls_dim), requires_grad=True) # (2, 10)
def forward(self, feature, m=1):
x = nn.functional.normalize(feature, dim=1) # (100, 2)
w = nn.functional.normalize(self.W, dim=0) # (2, 10)
cos_a = torch.matmul(x, w) / (torch.sqrt(torch.sum(torch.pow(x, 2))) * torch.sqrt(torch.sum(torch.pow(w, 2)))) # (100, 10)
s = torch.sqrt(torch.sum(torch.pow(x, 2))) * torch.sqrt(torch.sum(torch.pow(w, 2)))
a = torch.acos(cos_a) # 反三角函数得到的是弧度,1弧度=1*180°/3.14=57°
arc_softmax = torch.exp(s * torch.cos(a + m)) / (torch.sum(torch.exp(s * cos_a), dim=1, keepdim=True)
- torch.exp(s * cos_a) + torch.exp(s * torch.cos(a + m))) # (100, 10)
return arc_softmax
if __name__ == "__main__":
data = torch.randn(100, 2)
print(data, data.shape)
arc = ArcNet(2, 10)
out = arc(data, m=1)
print(out, out.shape)
import torch
import torch.nn as nn
from arc_softmax_net import ArcNet
class Net(nn.Module):
def __init__(self):
super().__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 32, 5, 1, 2), # (32, 28, 28)
nn.BatchNorm2d(32),
nn.PReLU(),
nn.Conv2d(32, 32, 5, 1, 2), # (32, 28, 28)
nn.BatchNorm2d(32),
nn.PReLU(),
nn.MaxPool2d(2, 2), # (32, 14, 14)
nn.Conv2d(32, 64, 5, 1, 2), # (64, 14, 14)
nn.BatchNorm2d(64),
nn.PReLU(),
nn.Conv2d(64, 64, 5, 1, 2), # (64, 14, 14)
nn.BatchNorm2d(64),
nn.PReLU(),
nn.MaxPool2d(2, 2), # (64, 7, 7)
nn.Conv2d(64, 128, 5, 1, 2), # (128, 7, 7)
nn.BatchNorm2d(128),
nn.PReLU(),
nn.Conv2d(128, 128, 5, 1, 2), # (128, 7, 7)
nn.BatchNorm2d(128),
nn.PReLU(),
nn.MaxPool2d(2, 2), # (128, 3, 3)
)
self.feature = nn.Linear(128*3*3, 2)
self.arc_softmax = ArcNet(2, 10)
def forward(self, x):
x = torch.reshape(self.layer1(x), (-1, 128*3*3))
feature = self.feature(x)
output = torch.log(self.arc_softmax(feature))
return feature, output
import torch
from my_net import Net
import torch.nn as nn
from torchvision import transforms, datasets
import os
from tools.utils import visualize
class Trainer:
def __init__(self):
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.net = Net().to(self.device)
self.save_path = "models/net.pth"
self.img_path = "images"
self.loss_fn = nn.NLLLoss()
self.optimizer = torch.optim.Adam(self.net.parameters())
self.mean, self.std = self.mean_std()
self.dataLoader = self.data_loader()
def mean_std(self):
sets = datasets.MNIST("datasets/", train=True, download=True, transform=transforms.ToTensor())
loader = torch.utils.data.DataLoader(sets, batch_size=len(sets), shuffle=True)
data = next(iter(loader))[0]
mean = round(torch.mean(data, dim=(0, 2, 3)).item(), 3)
std = round(torch.std(data, dim=(0, 2, 3)).item(), 3)
return mean, std
def data_loader(self):
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((self.mean,), (self.std,))
])
dataSet = datasets.MNIST("datasets/", train=True, download=True, transform=transform)
dataLoader = torch.utils.data.DataLoader(dataSet, batch_size=100, shuffle=True, num_workers=4)
return dataLoader
def train_test(self):
if not os.path.exists(self.img_path):
os.mkdir(self.img_path)
if os.path.exists(self.save_path):
self.net.load_state_dict(torch.load(self.save_path))
else:
print("NO {}".format(self.save_path))
epoch = 0
while True:
feature_loader = []
label_loader = []
for i, (x, y) in enumerate(self.dataLoader):
x = x.to(self.device)
y = y.to(self.device)
feature, output = self.net(x)
loss = self.loss_fn(output, y)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
feature_loader.append(feature)
label_loader.append(y)
if i % 100 == 0:
print("epoch:", epoch, "i:", i, "arc_softmax_loss:", loss.item())
features = torch.cat(feature_loader, dim=0)
labels = torch.cat(label_loader, dim=0)
visualize(features.data.cpu().numpy(), labels.data.cpu().numpy(), epoch)
torch.save(self.net.state_dict(), self.save_path)
epoch += 1
if epoch == 100:
break
if __name__ == "__main__":
trainer = Trainer()
trainer.train_test()
import matplotlib.pyplot as plt
def visualize(features, labels, epoch):
colors = ["#ff0000", "#ffff00", "#00ff00", "#00ffff", "#0000ff",
"#990000", "#999900", "#009900", "#009999", "#000099"]
plt.clf()
for i in range(10):
plt.plot(features[labels == i, 0], features[labels == i, 1], ".", c=colors[i])
plt.legend(["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"], loc="upper right")
plt.title("epoch=%d" % epoch)
plt.savefig("images/epoch=%d" % epoch)
问题:
解决梯度爆炸:
1、重新训练更新初始权值
2、调整学习率