解析unordeded_map和unordeded_set的底层实现
//本代码全部编辑于win10底下的vs2013编译器
在上一篇文章里边,我讲解了map和set的简单用法,以及简单的剖析了map和set的底层实现。
那么,现在就简单的对unordered_map和unordered_set做以简单的剖析。
其实,在STL函数库里边有关map和set的总共有8个函数。
map\set\multimap\multiset\unordered_map\unordered_set\unordered_multiset\unordered_multimap(8个)
简单的做以区分:
map:K/V结构。
set:K结构。
multi:可以冗余,如没有这个关键字,则是防冗余版本。
unordered:底层由哈希表(哈希桶算法)来实现,如无该关键字,则底层是由红黑树来实现。
现在想着重讲一下unordered_map和unordered_set,由于这两个用法类似(主要区别是结构不一样)。主要讲解unordered_map。
首先,unordered_map的底层是一个防冗余的哈希表(采用除留余数法)。
重所周知,哈希表的主要问题在于处理哈希冲突。
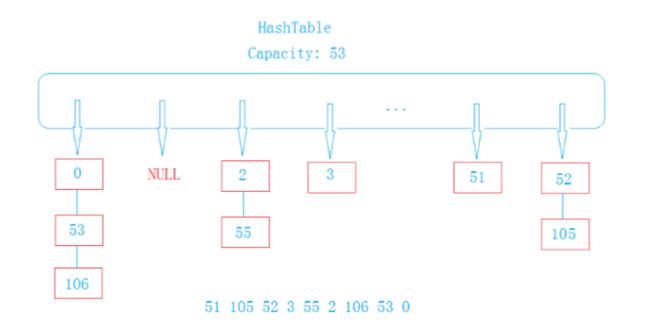
处理哈希冲突的方法很多:开链法(所谓的哈希桶)(主要讲解哈希桶,其他的方法就不在这里列举)
那么什么是开链法?其底层结构又是什么样子呢?
template //每个节点的结构
struct HashNode
{
pair _kv;
HashNode* _next;
HashNode(pair p)
:_next(NULL)
, _kv(p)
{}
};
template> //哈希表的结构,第三个参数是仿函数,为了实现可以存储string
class HashTable
{
protected:
vector _table;
size_t _size;
};
这就是它的底层结构!
1.用一个vector来作为一个指针数组来存储节点的指针,_size来保存当前哈希表中的有效元素个数。
2.由于是K/V结构,所以选择一个pair的结构来存储K/V。
3.vector中的每一个元素都指向一个链表,所有节点中需要一个next域的指针来指向下一个节点(采用单链表表结构)。
4.采用模板来实现哈希表可以存储任意数据类型的目的。
5.使用了仿函数技术(此处先暂不讲解原因)。
vector中不存储节点而存储节点指针的原因:首先考虑到指针占的内存比较小,不管是什么类型的数据,其指针都只占4个字节(32位下)。其次,如果直接存节点,那么假如,该列没有任何一个元素,那么其将存储一个无用的节点,那么还需要来区分到底是有效节点还是无效节点。比较复杂,所以存储节点的指针,如果该列无数据,则指针为空。
那么,哈希表最重要的就是增删查改了。
在这里,采用除留余数法进行数据的插入。(当前的key值%vector的大小,取其余数作为vector中的下标,从而定位该数据存储的位置)。
1.Insert
在这之前,我将引入一个叫做负载因子(载荷因子)的概念。
其作用就是:由于哈希表的时间复杂度为O(1),如果数据太多,而在vector的空间不变的情况下,势必每个指针下边挂的数据会越来越多,那么在查找的时候就势必要遍历这个链表,从而效率大打折扣,那么一般规定载荷因子的值为1(哈希表的有效元素个数最多达到vector的大小),一旦超出,则将进行扩容操作。
那么,我的做法就是:每次插入前先进行容量检测(单独实现一个函数完成),然后通过除留余数法定位(单独实现一个函数完成,这里有问题,如果是int则没有问题,后边将会解决这个问题),其次再被定位的这一列遍历整个链表(防冗余),如不冗余则进行头插(尾插也可以)。
pair Insert(const pair& p) //防冗余
{
if (_size == _table.size())//控制负载因子为1,当负载因子超过1时,进行扩容
{
CheckCapacity();
}
size_t index = GetIndex(p.first); //定位下标,除留余数法
Node* cur = _table[index];
while (cur)
{
if (cur->_kv.first == p.first) //防冗余
{
return make_pair(cur, false);
}
cur = cur->_next;
}
Node* tmp = new Node(p);
tmp->_next = _table[index]; //头插
_table[index] = tmp;
++_size;
return make_pair(_table[index], true);
}
这里先不要管其返回值为什么这么设计,等会会一一解释。
那么,下边是扩容的函数和除留余数法定位函数。
const size_t GetIndex(const K& key) const //除留余数法定位(使用了仿函数)
{
HashFunc hf;
size_t hash = hf(key);
return hash % _table.size();
}
void CheckCapacity()//扩容
{
HashTable ht(_table.size());
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
while (cur)
{
ht.Insert(cur->_kv);
cur = cur->_next;
}
}
_table.swap(ht._table);
}
首先,为什么使用除留余数法求下标的时候,要采用仿函数呢?
原因就是:如果插入的数据为string类型,那么string类型的数据是不能求模取余的。因此需要字符串哈希算法来完成转化。
因此为了实现string的数据存储,就必须使用仿函数来完成模板中不同类型对象的推演。并且利用模板参数,以及特化来实现。
而模板的推演会匹配与自己类型最接近那份代码,然后生成相应代码。
template
struct _HashFunc
{
size_t operator()(const K& key)
{
return key;
}
};
template<> //模板的特化
struct _HashFunc
{
size_t operator()(const string& key)
{
return BKDRHash(key.c_str());
}
size_t BKDRHash(const char* str) //字符串哈希算法
{
register size_t hash = 0;
while (*str)
{
hash = hash * 131 + *str;
str++;
}
return hash;
}
};
为了讲Insert然后讲到了扩容和除留余数法定位,讲到除留余数又讲到了定位下标为了保证stirng类型的数据成功存储,又讲到了之前哈希表结构中第三个的模板参数以及仿函数和模板的特化。
那么,扩容是怎么实现的呢?
大家看这个代码,是不是觉得疑问百出?为什么这么写就可以实现扩容,而且将数据一一复制过去,并且还没有释放原来的空间,这到底是为什么呢?
其实,如果你懂operator=()这个函数的现代写法的话,就可以很容易看懂上边的代码。
首先,看一段string类的operator=()重载代码。
String& operator=(const String& s)
{
if (this != &s)
{
String str(s._ptr);
swap(_ptr,str._ptr);
}
return *this;
}
看这个代码是不是和上边扩容的代码很像呢?都是创建了一个临时变量,然后对该临时变量进行赋值,然后交换这个临时变量和当前对象的指针。
交换了之后,原来this的空间已经由这个临时变量来管理,出了作用域临时变量会自己析构(这就是不用释放空间的原因)。
还要注意的一点就是:总结显示,如果哈希表的大小为一个质数,则会讲题哈希冲突的概率。
质数表:
unsigned long GetNextSize(unsigned long size) //使用素数作为哈希表的大小可以减少哈希冲突
{
const int _PrimeSize = 28;
static const unsigned long _PrimeList[_PrimeSize] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
for (int i = 0; i < _PrimeSize; ++i)
{
if (_PrimeList[i] > size)
{
return _PrimeList[i];
}
}
return 0;
}
2.Find
查找其实很简单啦!只需要对被查找数进行定位然后遍历该位置的单链表就可以啦。
Node* Find(const K& key)
{
size_t index = GetIndex(key);
Node* cur = _table[index];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return NULL;
}
3.Erase
对于删除操作,其实坑挺多的,这里要注意啦。
大家是不是想,既然我写了Find函数,那么我就直接用Find来查找这个被删的值,如果找到了Find就会返回一个该节点的指针,然后在删除不就ok了。
其实这么想就错了。这里是不能这么做的。
因为,只能拿到被删节点的指针,而该节点位于单链表中,必须拿到其前一个节点的指针才可以删除当前节点。
那么,有的人又想到假删除(链表面试题(删除一个单链表中的非尾节点,要求只能遍历一次)),其方法就是吧当前节点的下一个节点的值拷贝给当前节点,然后删除当前节点的下一个节点。看似能完成,那么,如果要删除的是尾节点,又该怎么办呢?
有的人又提出,如果是尾节点就和第一个节点进行交换。那么这样是不是很麻烦呢!而我们起初为了调用Find还不是为了简单才调用它的吗?
那么,还不如我们按步就搬。
bool Erase(const K& key)
{
size_t index = GetIndex(key);
Node* cur = _table[index];
Node* prev = NULL;
while (cur)
{
if (cur->_kv.first == key)
{
if (prev == NULL)
{
_table[index] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
--_size;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
这样,也不会出现很多问题。
以上就是哈希表的简单操作,当然远远不止这些。最重要的还属其迭代器的实现了(比较精妙)。
这里先给出其代码,以后再做讲解。
而unordered_map的借口则是分别调用哈希表的所有接口。
完整代码:
#pragma once //unordered_map的底层
#include
#include
template
struct HashNode
{
pair _kv;
HashNode* _next;
HashNode(pair p)
:_next(NULL)
, _kv(p)
{}
};
template //声明
class HashTable;
//stl库里边是没有使用Ref和Ptr来达到代码复用的目的。而是将const和非const迭代器分开来写。
//具体原因在于新加的那个哈希表指针,我自己又将其该为const的,暂时没有发现问题
template
struct HashTableIterator
{
typedef HashTableIterator Self;
typedef HashTable HashTable;
typedef HashNode Node;
HashTableIterator(){}
HashTableIterator(Node* ptr, const HashTable* table)
: _ptr(ptr)
, _hashtable(table)
{}
Ref operator*()
{
return _ptr->_kv;
}
Ptr operator->()
{
return &(operator*());
}
Self& operator++()
{
_ptr = _Next(_ptr);
return *this;
}
Self operator++(int)
{
Self tmp = *this;
++*this;
return tmp;
}
bool operator==(const Self& s)
{
return _ptr == s._ptr;
}
bool operator!=(const Self& s)
{
return _ptr != s._ptr;
}
Node* _ptr;
const HashTable* _hashtable;
protected:
/* Node* _Next(Node* cur)
{
assert(cur);
Node* old = cur;
cur = cur->_next;
if (!cur)
{
size_t index = _hashtable->GetIndex(old->_kv.first);
while (!cur && ++index < _hashtable->_table.size()) //需要友元
cur = _hashtable->_table[index];
}
return cur;
}*/
Node* _Next(Node* cur)
{
assert(cur);
Node* old = cur;
cur = cur->_next;
if (!cur)
{
size_t index = _hashtable->GetIndex(old->_kv.first);
while (!cur && ++index < _hashtable->GetTable()->size())
cur = _hashtable->GetTable()->operator[](index);
}
return cur;
}
};
template
struct _HashFunc
{
size_t operator()(const K& key)
{
return key;
}
};
template<>
struct _HashFunc
{
size_t operator()(const string& key)
{
return BKDRHash(key.c_str());
}
size_t BKDRHash(const char* str) //字符串哈希算法
{
register size_t hash = 0;
while (*str)
{
hash = hash * 131 + *str;
str++;
}
return hash;
}
};
template>
class HashTable
{
typedef HashNode Node;
public:
typedef HashTableIterator&, pair*> Iterator;
typedef HashTableIterator&, const pair*> ConstIterator;
public:
HashTable()
:_size(0)
{}
HashTable(size_t size)
:_size(0)
{
_table.resize(GetNextSize(size));
}
pair Insert(const pair& p) //防冗余
{
if (_size == _table.size())//控制负载因子为1,当负载因子超过1时,进行扩容
{
CheckCapacity();
}
size_t index = GetIndex(p.first);
Node* cur = _table[index];
while (cur)
{
if (cur->_kv.first == p.first)
{
return make_pair(cur, false);
}
cur = cur->_next;
}
Node* tmp = new Node(p);
tmp->_next = _table[index];
_table[index] = tmp;
++_size;
return make_pair(_table[index], true);
}
Node* Find(const K& key)
{
size_t index = GetIndex(key);
Node* cur = _table[index];
while (cur)
{
if (cur->_kv.first == key)
{
return cur;
}
cur = cur->_next;
}
return NULL;
}
bool Erase(const K& key)
{
size_t index = GetIndex(key);
Node* cur = _table[index];
Node* prev = NULL;
while (cur)
{
if (cur->_kv.first == key)
{
if (prev == NULL)
{
_table[index] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
--_size;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
V& operator[](const K& key)
{
pair ret;
ret = Insert(make_pair(key,V()));
return ret.first->_kv.second;
}
Iterator Begin()
{
for (size_t i = 0; i < _table.size(); ++i)
if (_table[i])
return Iterator(_table[i], this);
return End();
}
Iterator End()
{
return Iterator(NULL,this);
}
ConstIterator Begin() const
{
for (size_t i = 0; i < _table.size(); ++i)
if (_table[i])
return ConstIterator(_table[i], this);
return End();
}
ConstIterator End() const
{
return ConstIterator(NULL, this);
}
~HashTable()
{
Clear();
}
void Clear()
{
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
Node* del = NULL;
while (cur)
{
del = cur;
cur = cur->_next;
delete del;
}
_table[i] = NULL;
}
}
const size_t GetIndex(const K& key) const
{
HashFunc hf;
size_t hash = hf(key);
return hash % _table.size();
}
const vector* GetTable() const
{
return &_table;
}
protected:
void CheckCapacity()
{
HashTable ht(_table.size());
for (size_t i = 0; i < _table.size(); ++i)
{
Node* cur = _table[i];
while (cur)
{
ht.Insert(cur->_kv);
cur = cur->_next;
}
}
_table.swap(ht._table);
}
unsigned long GetNextSize(unsigned long size) //使用素数作为哈希表的大小可以减少哈希冲突
{
const int _PrimeSize = 28;
static const unsigned long _PrimeList[_PrimeSize] =
{
53ul, 97ul, 193ul, 389ul, 769ul,
1543ul, 3079ul, 6151ul, 12289ul, 24593ul,
49157ul, 98317ul, 196613ul, 393241ul, 786433ul,
1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,
50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,
1610612741ul, 3221225473ul, 4294967291ul
};
for (int i = 0; i < _PrimeSize; ++i)
{
if (_PrimeList[i] > size)
{
return _PrimeList[i];
}
}
return 0;
}
protected:
vector _table;
size_t _size;
};