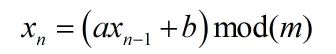Random 类源码分析

Random 类

用于生成伪随机数的流。 该类使用48位种子，其使用线性同余公式进行修改

• 许多应用程序会发现方法Math.random()使用起来更简单。
• java.util.Random的java.util.Random是线程安全的。 但是，跨线程的同时使用java.util.Random实例可能会遇到争用，从而导致性能下降。 在多线程设计中考虑使用ThreadLocalRandom 。
• java.util.Random的java.util.Random不是加密安全的。 考虑使用SecureRandom获取一个加密安全的伪随机数生成器，供安全敏感应用程序使用。

Random 类中有两个构造函数

• Random（）：创建一个新的随机数生成器
• random（long seed）：使用单个 Long 种子创建一个新的随机数生成器

测试输出多次带种子的会发现伪随机数的规律，原来感觉高大上的东西原来就像一个数组，那得扒一扒里面的东西了

Random random1 = new Random(10);
System.out.println(random1.nextInt(10)); // 3
System.out.println(random1.nextInt(10)); // 0
Random random2 = new Random(10);
System.out.println(random2.nextInt(10)); // 3
System.out.println(random2.nextInt(10)); // 0
// 多测了几次还是这样，那应该不是电脑的问题

点开带种子构造函数源码看看，会发现不是明白，那就先回到无参构造函数的情况

public Random(long seed) {
    if (getClass() == Random.class)
        this.seed = new AtomicLong(initialScramble(seed));
    else {
        // subclass might have overriden setSeed
        this.seed = new AtomicLong();
        setSeed(seed);
    }
}

无参构造random（）

无参构造函数按照上面的方式输出是随机数，并且每次不同

public Random() {
    this(seedUniquifier() ^ System.nanoTime());
}

先看能看懂的 ，System.nanoTime() 获取电脑时间通过,下面是对应的源码，但是native系统调用方法，实现源码没有，只能看文档了

public static native long nanoTime(); 
/* // 来源百度翻译
返回正在运行的Java虚拟机的高分辨率时间源的当前值，以纳秒为单位。
此方法只能用于测量经过的时间，并且与系统或挂钟时间的任何其他概念无关。返回的值表示纳秒，因为某些固定的任意原点时间 （可能在将来，因此值可能为负）。

在Java虚拟机的实例中，所有对此方法的调用都使用相同的源;其他虚拟机实例可能使用不同的源。 此方法提供纳秒级精度，但不一定是纳秒级分辨率（即值的变化频率） 
- 除了分辨率至少与currentTimeMillis（）的分辨率一样好之外，不做任何保证。
连续调用的差异超过大约292年（2^63纳秒）将无法正确计算由于数值溢出而导致的经过时间。 只有在计算在Java虚拟机的同一实例中获得的两个此类值之间的差异时，此方法返回的值才有意义。
例如，要测量某些代码执行所需的时间：
long startTime = System.nanoTime（）; // ...正在测量的代码...... long estimatedTime = System.nanoTime（） -  startTime; 比较两个纳米时间值 
long t0 = System.nanoTime（）; ... long t1 = System.nanoTime（）;
一个应该使用t1 - t0 <0，而不是t1 

大概总结一下文档的意思：

这个函数能够返回一个正在运行的当前虚拟机的时间源值，单位为纳秒
此方法只能用于测量经过的时间，并且与系统或挂钟时间的任何其他概念无关。
在Java虚拟机的实例中，所有对此方法的调用都使用相同的源;其他虚拟机实例可能使用不同的源。

这个函数再内在的东西就没有探究了，只要知道这个是获取一个纳秒值，因为精确度变化很大，相对于的这个方法上面一行还有一个对应的

public static native long currentTimeMillis();
// 这个就不做解释了，这个性能稍微低一点，文档上这个获取的时间值精确度相对低一点

知道了这个是获取一个系统的比较精确的值（也比较随机），再看一下 seedUniquifier()

private static long seedUniquifier() {
    // L'Ecuyer, "Tables of Linear Congruential Generators of
    // Different Sizes and Good Lattice Structure", 1999
    // 线性同余生成元表  // 不同尺寸和良好的晶格结构”，1999年
    for (;;) {
        long current = seedUniquifier.get();
        long next = current * 181783497276652981L; 
        // 两个很大的数相乘
        if (seedUniquifier.compareAndSet(current, next))
            // 这个比较并且交换 也是一个 Juc 里面的值
            // 比较当前工作内存中的值和主内存中的值，如果这个值是期望的，那么则执行操作！如果不是就 一直循环！，就是为了保证即使在多线程的环境中返回的也是不同的数
            return next;
    }
}
// 进入到一个死循环，看一下 seedUniquifier 
 private static final AtomicLong seedUniquifier
        = new AtomicLong(8682522807148012L);
// atomic 这个是 juc 里面修饰的原子性的 long ，get方法说就是获得这个构造函数里面的值

主要的东西在代码注释里面，就是如果 JUC 不太懂的话就只要知道这个是返回了一个很大的即使在多线程环境里也是很随机的数。

再回到无参构造函数

public Random() {
    this(seedUniquifier() ^ System.nanoTime());
} 
// 又调用回了刚开始讲的有参构造函数 
//this (种子是seedUniquifier() 与System.nanoTime()按位异或的结果)

有参构造

天道好轮回我又回来了

public Random(long seed) {
    if (getClass() == Random.class)
        this.seed = new AtomicLong(initialScramble(seed));
    else {
        // subclass might have overriden setSeed 这个说子类可能重写了这个不考虑
        this.seed = new AtomicLong(); // 创建一个新的AtomicLong，初始值为 0 
        setSeed(seed);
    }
}

// 下面就只有一个方法了 setSeed（seed），不点开来看看都对不起人
   synchronized public void setSeed(long seed) {
        this.seed.set(initialScramble(seed));
        haveNextNextGaussian = false; 
    }

   private static long initialScramble(long seed) {
        return (seed ^ multiplier) & mask;
    }

	private static final long multiplier = 0x5DEECE66DL;
	private static final long mask = (1L << 48) - 1;
	// x & [(1L << 48)–1]与 x（mod 2^48）等价 取低位48位
/*
通过将种子自动更新为 (seed ^ 0x5DEECE66DL) & ((1L < < 48) - 1)并清除nextGaussian()使用的haveNextNextGaussian 标志，Random 类可实现 setSeed 方法。  
Random 类实现的 setSeed 恰好只使用 48 位的给定种子。  
但是，通常重写方法可能使用 long 参数的所有 64 位作为种子值。  
随机数种子就是产生随机数的第一次使用值，将这个种子的值转化为随机数空间中的某一个点上，并且产生的随机数均匀的散布在空间中。 以后产生的随机数都与前一个随机数有关。
*/

这个最后原理找到线性同余法（前面都懂了这个函数和数值的转换关系这个我没太懂）

• 种子x0
• 模数m
• 乘数a
• 常数b

JDK 文档中讲具体见 Donald Knuth 的“计算机编程艺术”，第2卷 ，第3.2.1节 我找到了这本书，对不起我不配，看一偶。

next（）

姑且当懂了种子数的原理，就是在不指定种子是让种子随机，然后通过这个计算处理来，下面来看如何获取随机数
获取的随即数的值不一一看了，都是调用 protected int next(int bits)

// 几个常量我贴出来好理解
private static final long multiplier = 0x5DEECE66DL;
private static final long addend = 0xBL;
private static final long mask = (1L << 48) - 1;
protected int next(int bits) {
    long oldseed, nextseed;
    AtomicLong seed = this.seed;
    do {
        oldseed = seed.get();
        nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.compareAndSet(oldseed, nextseed));
    return (int)(nextseed >>> (48 - bits));
}
// 汇聚一下
nextseed = (oldseed * multiplier + addend) & mask;

// 老的种子乘以一个数multiplier加上addend 然后相与取低位48作为结果。

这个相当于线性同余法函数，就可以得到下一个48位的随机数，到数学了理解的就不多了

总结

如果对线性同余法感兴趣的可以去了解懂后再回看这个文章应该会很有体会

然后只需要最终原理是，随机数是需要一个种子，种子只要固定，随机数的序列就固定，然后默认构造函数中的种子就可以理解为是一个真正的随机数。

说实话我只是想复习复习这个Random类的，然后就发现了奇怪的东西，然后就点进去了。。