webrtc的拥塞控制之trendline filter分析

 首先说明，本文基于[1]，这篇文章是由学霸君的工程师写的，但是有些小的错误。原作者直接将webrtc中的拥塞控制采用c重写了，代码见[2]。之前在网上也读过大牛的一些文章[3].
 webrtc最早的拥塞控制算法分为两个部分，在发送端运行基于丢包的拥塞器，而在接收端部署基于时延的拥塞控制算法。数据包单向时延差信息（单向时延梯度），可以反映网络链路拥塞程度，可以参看原作者的论文[4]。早期的算法，采用kalman滤波获取网络拥塞信号，[5]有详细的分析。基于kalman滤波获取拥塞信号的方式，后来被废弃了。
 拥塞控制的基本方法就是，发送端根据网络状态，动态改变发送速率，适配网络中的可用带宽。
 数据帧$i$的发送时刻，接收时刻分别是$T_i,t_i$。GCC[7]中建立的网络延迟模型为：
$$\begin{array}{rl}{d}_m(t_i)& =(t_i-t_{i-1})-(T_i-t_{T-1})\\ & =\frac{\Delta L(t_i)}{C(t_i)}+m(t_i)+n\end{array}$$
 kalman中的两个状态，由此可得：
$$\theta =\left[\begin{array}{c}\frac{1}{C(t_i)}\\ m(t_i)\end{array}\right]$$
 [7]中有一系列的推导，用kalman的方式对这两个信号进行更新。其中，$C(t_i)$指的是瓶颈链路总的带宽，比如骨干网的带宽40Gbps，获取这个信号其实没啥意义。$m(t_i)$反映的就是队列消涨情况。[4]就对状态方程进行了小小的更新。最早的L就是视频帧的大小，而后来更新为一段时间内（比如5ms）向网络中发送的数据量。这样两个时间段，收到的数据量，近似相等。于是$\Delta L(t_i)=0$，状态方程直接就退化为[4]：
$$d_m(t_i)=m(t_i)+n$$
 依然是采用kalman的方式，根据测量值对实际值进行估计。这里的估计过程，实质上就是一个exponential filter。因为有一堆公式的包装，瞬间就显得高大上了。
 webrtc将拥塞控制逻辑全部移到了发送端，另外采用trendline filter的方式获取网络拥塞信号，在博文[6]里有一些描述。方法变了，但是核心思想没有变化，通过观测网络链路中的排队队列的消涨情况，判断链路是否拥塞，进而调节速率。
 [1]中有这样一段话,可以参考原文中的图例:

基于延迟的拥塞控制是通过每组包的到达时间的延迟差（delta delay）的增长趋势来判断网络是否过载，如果过载进行码率下调，如果处于平衡范围维持当前码率，如果是网络承载不饱满进行码率上调。这里有几个关键技术:包组延迟评估、滤波器趋势判断、过载检测和码率调节

 其中重要的一点，根据5ms时间间隔对回馈的数据包分组，这个概念可以近似认为论文[7]中帧的概念。我很早就觉得以视频帧为单位的队列时延信息求解不合适，因为在视频传输中，I，P，B帧的差异很大，这样会引入误差。而基于时间段进行组的划分，要好很多，由于pacer的作用，在一小段时间内，可以认为数据包是均匀向外发送的，对网络状态进行观测。
 feedback数据包到来后，接收端的处理函数：

void DelayBasedBwe::IncomingPacketFeedback(
    const PacketFeedback& packet_feedback) {
      if (inter_arrival_->ComputeDeltas(timestamp, packet_feedback.arrival_time_ms,
                                    now_ms, packet_feedback.payload_size,
                                    &ts_delta, &t_delta, &size_delta)) {
    double ts_delta_ms = (1000.0 * ts_delta) / (1 << kInterArrivalShift);
    trendline_estimator_->Update(t_delta, ts_delta_ms,
                                 packet_feedback.arrival_time_ms);
    detector_.Detect(trendline_estimator_->trendline_slope(), ts_delta_ms,
                     trendline_estimator_->num_of_deltas(),
                     packet_feedback.arrival_time_ms);
  }
    }

 detector_.Detect()，计算网络的过载情况。trendline_estimator_->trendline_slope()获取回归方程的斜率。
 组与组之间的时延信息计算如下:

*timestamp_delta =current_timestamp_group_.timestamp -prev_timestamp_group_.timestamp;
*arrival_time_delta_ms = current_timestamp_group_.complete_time_ms -prev_timestamp_group_.complete_time_ms;
//InterArrival::ComputeDeltas

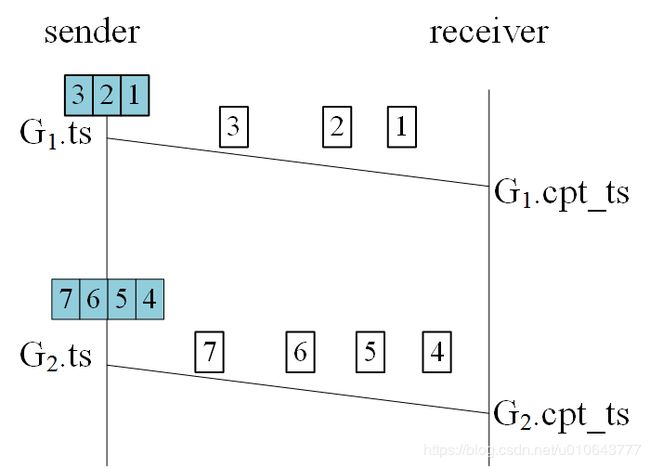
 盗用[1]中的一个图,对上面两行代码进行解释。我对原有的图片进行修正，在发送端，pacer均匀地向网络注入数据包，但是经过中间的路由器，由于存在其他数据流的包，这些数据包之间的间隔就错落开来。
$timestamp\_delta=G2.ts-G1.ts$
$arrival\_time\_delta\_ms=G2.cpt\_ts-G1.cpt\_ts$
 若数据包属于新的分组，则对trendline filter进行更新：

void TrendlineEstimator::Update(double recv_delta_ms,
                                double send_delta_ms,
                                int64_t arrival_time_ms) {
  const double delta_ms = recv_delta_ms - send_delta_ms;//①
  if (first_arrival_time_ms == -1)
    first_arrival_time_ms = arrival_time_ms;

  // Exponential backoff filter.
  accumulated_delay_ += delta_ms;    
  smoothed_delay_ = smoothing_coef_ * smoothed_delay_ +
                    (1 - smoothing_coef_) * accumulated_delay_;  
    // Simple linear regression,表明trendline是线性回归。
  delay_hist_.push_back(std::make_pair(
      static_cast(arrival_time_ms - first_arrival_time_ms),smoothed_delay_)); //②  
  if (delay_hist_.size() == window_size_) {
    // Only update trendline_ if it is possible to fit a line to the data.
    trendline_ = LinearFitSlope(delay_hist_).value_or(trendline_);//③线性回归
  }     
                                }

 Update函数中参数recv_delta_ms就是计算得到的arrival_time_delta_ms，而send_delta_ms就是arrival_time_delta_ms，arrival_time_ms就是本组内最后一个包的接收端到达时间G2.complete_time_ms。在网络链路排队的数据包在消减的情况，delta_ms值是可能为负的。
 这段代码在[1]中有公式表示。其中代码中标号①计算的时间为相邻组的接收间隔与发送间隔的差值。
$d(i)=(G_i.cpt\_ts-G_{i-1}.cpt\_ts)-(G_i.ts-G_{i-1}.ts)....(3)$
$acc\_delay(i)={\sum }_{j=1}^{i}d(j)....(4)$。
 最后进行平滑计算，这是老套路了:
$smoothed\_delay\_(i)=smoothing\_coef\_\ast smoothed\_delay\_(i-1)+(1-smoothing\_coef\_)\ast acc\_delay(i)....(5)$
 smoothed_delay_反映的就是数据包经由网络链路的排队时延信息，反映的是网络排队队列的消涨情况。重要的是，它最后储存的数据数在标号②，就是本分组的最后一个包的到达时刻与第一个分组到达时刻的差值(x轴)，smoothed_delay_(y轴)。在标号③除，当收集到足够的数据的时候，对数据进行线性回归，求取曲线的斜率。这个数据的处理过程，就等效原论文[4]里中m值。
 它的回归方程斜率的求解如下:
$k=\frac{\sum (x_i-x_{avg})(y_i-y_{avg})}{\sum (x_i-x_{avg}{)}^2}....(6)$

rtc::Optional LinearFitSlope(
    const std::deque>& points) {
  RTC_DCHECK(points.size() >= 2);
  // Compute the "center of mass".
  double sum_x = 0;
  double sum_y = 0;
  for (const auto& point : points) {
    sum_x += point.first;
    sum_y += point.second;
  }
  double x_avg = sum_x / points.size();
  double y_avg = sum_y / points.size();
  // Compute the slope k = \sum (x_i-x_avg)(y_i-y_avg) / \sum (x_i-x_avg)^2
  double numerator = 0;
  double denominator = 0;
  for (const auto& point : points) {
    numerator += (point.first - x_avg) * (point.second - y_avg);
    denominator += (point.first - x_avg) * (point.first - x_avg);
  }
  if (denominator == 0)
    return rtc::Optional();
  return rtc::Optional(numerator / denominator);
}

 接收端，每间隔RemoteEstimatorProxy::kDefaultSendIntervalMs = 100ms，发送一次feedback报文。
 但是根据我在ns3上的仿真结果[8]，当可用带宽较高时，GCC不太稳定。也有可能是我的仿真结果有误。这个算法里面的有两个超参数$k_{up},k_{down}$。难以解释。我觉得拥塞控制，tunable的参数应该越少越好。
 这种基于trend作为拥塞控制信号思想，在10年的论文，就有基本雏形[9]。
 下面给个具体的分析，单向时延信号是我从cubic仿真中获取的，仿真代码[10]。我只计算了acc_delay，对单向时延信号进行调和级数滤波。
 信号处理代码：
trend.py

import os
class HarmnicMean(object):
    def __init__(self,window):
        self.w=window
        self.c=0
        self.his=[]
    def newSample(self,s):
        mean=0.0
        sample=float(s)
        if self.c==0:
            mean=sample
        if sample>0:
            self.his.append(1000/sample)
            self.c+=1
        if self.c>self.w:
            a=self.his[self.c-self.w:]
            self.his=a
            if len(self.his)!=self.w:
                print "error"
            self.c=self.w
        if self.c

 调和级数滤波后的单向时延信号：

 累计时延梯度信号：

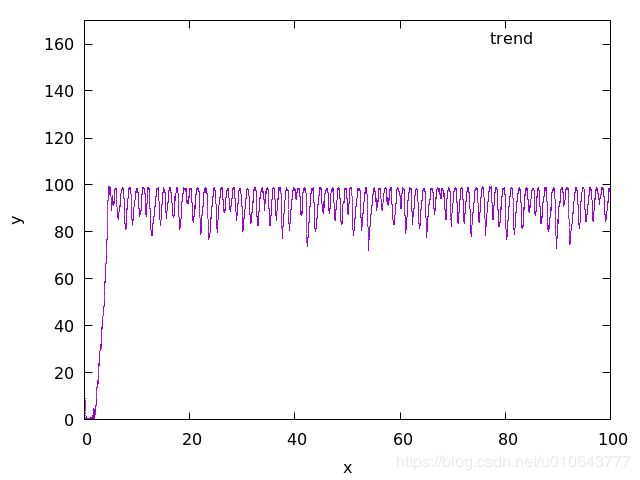
 累计时延梯度确实可以反映出网络中的队列的消涨情况。
 FBI WARNNIG：研究生小白，不要选拥塞控制相关的研究课题，这个研究领域基本处于停滞状态。因为从网络中可以获取的信号有限，也就限制可以玩出的花样。
[1]webRTC是怎么应对网络变化的
[2]razor https://github.com/yuanrongxi/razor
[3]如何实现1080P延迟低于500ms的实时超清直播传输技术
[4]Analysis and Design of the Google Congestion Control
for Web Real-time Communication
[5]WebRTC基于GCC的拥塞控制(上) - 算法分析
[6]WebRTC-GCC两种实现方案对比
[7] Congestion Control for Web Real-Time Communication
[8] rmcat-simulation-ns3
[9] Trend: A dynamic bandwidth estimation and adaptation algorithm for real-time video calling
[10] congstion simulation-Cubic, BBR, BBRv2
[11] WebRTC研究：Trendline滤波器-TrendlineEstimator