分类与回归树(classification and regression tree,CART)之回归
分类与回归树(classification and regression tree,CART)之回归
写在前面: 因为正在看提升树,所以又去看了李航老师《统计学习方法》的CART算法的回归部分,看完莫名想起了本科导师的名言:国内人写书,喜欢简单问题复杂化,复杂问题超级复杂化。可能是我境界不够,我不明白两个for循环的事情为何会叙述的如此复杂。。复杂到你可能得花费一些时间去思考他想表达什么,复杂到你看了一遍不知道他在讲什么。这篇博客我将用几句简短的话来叙述CART做回归时的方法,如果你没看懂那就是我的失败。。
这篇博客主要从以下几个方面来介绍:
- CART回归基本原理
- sklearn中CART实践
一、CART回归基本原理
分类与回归树CART是由Loe Breiman等人在1984年提出的,自提出后被广泛的应用。看这名字也知道CART既能用于分类也能用于回归,关于分类我们这里就不介绍了,因为和前面博客介绍的决策树相比较,CART除了把选择最优特征的方法从信息增益(率)换成了基尼指数,其他的没啥不同。这篇博客主要介绍CART用户回归任务。
下面我将用几句话来介绍CART的核心思想,主要讲CART是如何构造一棵树的,力求做到让人一下就看明白。

上面这个过程,相信一下就能看明白。但是这里会产生个问题:我们上面讲了要计算切分后的误差,那么这个误差怎么计算?
这个误差用的是均方误差来计算的,均方误差的话真实值是知道的,那么预测值是什么?在揭晓预测值之前先来形式化的定义下,不然不好描述。假设特征 j j j和切分点为 s s s,把样本划分为两部分 R 1 R_1 R1和 R 2 R_2 R2,每部分的预测值分别为 c 1 c_1 c1和 c 2 c_2 c2,则均方误差(损失函数)为:
(1) ∑ x i ∈ R 1 ( y i − c 1 ) 2 + ∑ x i ∈ R 2 ( y i − c 2 ) 2 \sum_{x_i \in R_1}(y_i - c_1)^2 + \sum_{x_i \in R_2}(y_i - c_2)^2 \tag{1} xi∈R1∑(yi−c1)2+xi∈R2∑(yi−c2)2(1)
我们的目标是要求 c 1 c_1 c1和 c 2 c_2 c2使得(1)式最小,也就是我们的优化目标为:
(2) min j , s [ min c 1 ∑ x i ∈ R 1 ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ R 2 ( y i − c 2 ) 2 ] \min_{j,s}[\min_{c_1}\sum_{x_i \in R_1}(y_i - c_1)^2 + \min_{c_2}\sum_{x_i \in R_2}(y_i - c_2)^2] \tag{2} j,smin[c1minxi∈R1∑(yi−c1)2+c2minxi∈R2∑(yi−c2)2](2)
我们来看下这个优化目标,先看下 min j , s \min_{j,s} minj,s里面的式子,也就是
(3) min c 1 ∑ x i ∈ R 1 ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ R 2 ( y i − c 2 ) 2 \min_{c_1}\sum_{x_i \in R_1}(y_i - c_1)^2 + \min_{c_2}\sum_{x_i \in R_2}(y_i - c_2)^2\tag{3} c1minxi∈R1∑(yi−c1)2+c2minxi∈R2∑(yi−c2)2(3)
因为是个加法,只要分别求两项的最小值即可,提到求最小值,那肯定就是来一波求导了,就拿 ∑ x i ∈ R 1 ( y i − c 1 ) 2 \sum_{x_i \in R_1}(y_i - c_1)^2 ∑xi∈R1(yi−c1)2来求吧,这个求导过程很简单就不写了,求出来:
(4) c 1 = 1 N 1 ∑ x i ∈ R 1 y i c_1 = \frac{1}{N_1}\sum_{x_i \in R_1}y_i \tag{4} c1=N11xi∈R1∑yi(4)
同理:
(5) c 2 = 1 N 2 ∑ x i ∈ R 2 y i c_2 = \frac{1}{N_2}\sum_{x_i \in R_2}y_i \tag{5} c2=N21xi∈R2∑yi(5)
里面的最小值知道了,外层的 min j , s \min_{j,s} minj,s就回到了我们开头写的两个for循环遍历了。。关于CART做回归构造树的过程就是这些了,至于剪枝就不讲了,和分类一样,有兴趣的可参考我以前的博客:决策树(decision tree)(二)——剪枝。
下面看个具体的例子,看看CART是如何构造回归树,并作出预测的。
训练数据集为(来自李航统计学习方法p75,说一下李航的这个数据集存在很大的问题,他75页给出的表格如下图所示,按照他书中符号的注释 x i x_i xi表示第 i i i个样本, x i ( j ) x_i^{(j)} xi(j)表示第 i i i个样本的第 j j j个特征,那么我们看下表,who can tell me 特征的取值是什么?):
| x i x_i xi | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| y i y_i yi | 4.50 | 4.75 | 4.91 | 5.34 | 5.80 | 7.05 | 7.90 | 8.23 | 8.70 | 9.00 |
所以,我这里自己添加了两个特征取值,见下表
| 样本编号 i i i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x i ( 1 ) x_i^{(1)} xi(1) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x i ( 2 ) x_i^{(2)} xi(2) | 0.1 | 0. 2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| y i y_i yi | 4.50 | 4.75 | 4.91 | 5.34 | 5.80 | 7.05 | 7.90 | 8.23 | 8.70 | 9.00 |
按照上面的算法步骤,两个for循环挑出最有特征的最优分裂点。
对于第一个特征,能够求出最优分裂点为 s = 5 s=5 s=5时,把10个样本分成了 R 1 = { 1 , 2 , 3 , 4 , 5 } R_1 =\{1,2,3,4,5\} R1={1,2,3,4,5}和 R 2 = { 6 , 7 , 8 , 9 , 10 } R_2 = \{6, 7, 8, 9, 10\} R2={6,7,8,9,10}, c 1 = 5.06 c_1 = 5.06 c1=5.06, c 2 = 8.176 c_2 = 8.176 c2=8.176,此时误差最小,误差为6.7。
对于第二个特征,能够求出最优分裂点为 s = 5 s=5 s=5时,把10个样本分成了 R 1 = { 1 , 2 , 3 , 4 , 5 } R_1 =\{1,2,3,4,5\} R1={1,2,3,4,5}和 R 2 = { 6 , 7 , 8 , 9 , 10 } R_2 = \{6, 7, 8, 9, 10\} R2={6,7,8,9,10}, c 1 = 5.06 c_1 = 5.06 c1=5.06, c 2 = 8.176 c_2 = 8.176 c2=8.176,此时误差最小,误差为6.7。
因为两个误差一样,所以可以任取一个特征,作为第一个分裂点(注:我这里只是举例演示,所以第二个特征只是把第一个特征缩小了10倍,这在特征选择里属于冗余特征,实际数据集中如果出现了这样的特征,也要删掉,因为提供不了任何信息)
下图为构建的树图:
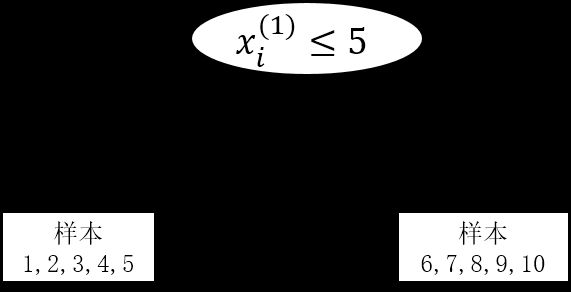
下面就是递归的去做,就不讲了。
最后这个回归模型的预测值为:
(6) f ( x ) = ∑ m = 1 M c m I ( x ∈ R m ) f(x) = \sum_{m=1}^Mc_mI(x \in R_m)\tag{6} f(x)=m=1∑McmI(x∈Rm)(6)
关于这个公式解释下,就是最终构建完一颗完整的树(剪枝)后,会把样本集划分为M个区域(就是M个叶子节点),当预测新样本时,按照构造好的决策树走到最后的叶子节点,然后取叶子节点里所有样本的平均值作为预测值(即上面的公式)。
二、sklearn中CART实践
sklearn中DecisionTreeRegressor则是封装的CART(做了些改进),我们可以直接调用,然后把构造的回归树画出来,让大家看的更清晰。
上代码:
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree
import graphviz
boston = load_boston()
regressor = DecisionTreeRegressor(random_state=0)
regressor.fit(boston.data[0:15, 0:3], boston.target[0:15])
dot_data = tree.export_graphviz(regressor, out_file=None)
graph = graphviz.Source(dot_data)
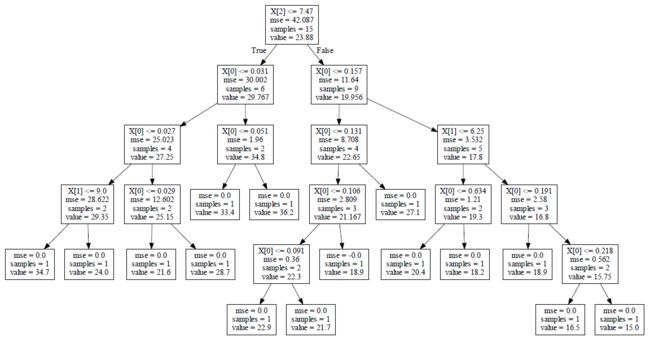
graph.render(filename="boston_dtr", directory="output")
这里为了演示的方便,我只用了15条样本,3个特征,不然画出来的树太大。画出来的回归树如下所示: