孩子现在的作业题是真难啊
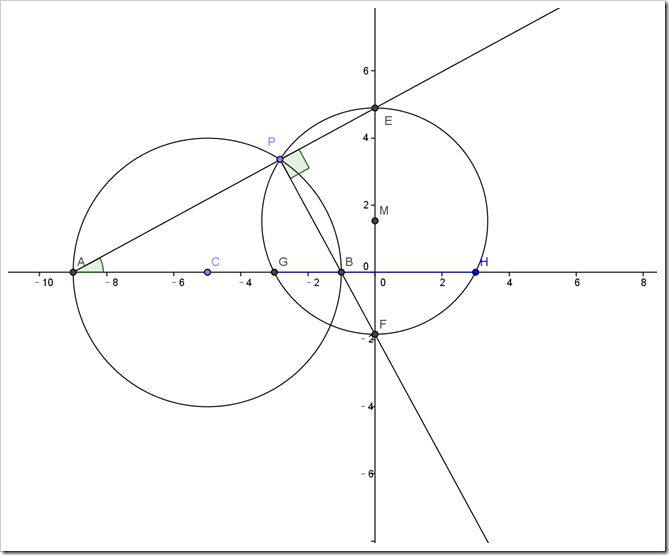
C(-5,0),以C为圆心作半径为4的圆,交x轴于A、B两点。P为圆上一个动点,AP交y轴于E,PB交y轴于F,以EF为直径作圆,交x轴于G、H两点,
求线段GH是否随着P的变化而改变,如果是不变的,求其长度。
(用GeoGebra作图,ggb作图文件)
一开始想找相似三角形,想用圆心角或圆周角的关系来求出GH,发现不好办。
后来又引入角PAB的变量,求出的E、F交点的式子也比较复杂。
后来才发现设PA直线的斜率为k,各种关系式及坐标都比较容易求出了,最后GH是与k无关的。
后来孩子告诉有个简便方法,通过相似能够解决。
三角形OBF与三角形OEA相似,OB/OF=OE/OA,所以OE*OF=OA*OB=9
而OG*OG=GM*GM-OM*OM=(GM+OM)*(GM-OM)=(ME+OM)*(FM-OM)=OE*OF=9
所以OG=3,GH=6。