集成学习(ensemble learning)(二)

接上一篇： 集成学习(ensemble learning)。
本篇对集成学习中的 Bagging 和 随机森林算法 进行总结。

一、Bagging原理

Bagging 的弱学习器之间没有依赖关系，可以并行计算。

1、随机采样（BootStrap）

自助法，即有放回的采样，也就是说，之前采集到的样本在放回后有可能继续被采集到。一般来讲，随机采样的样本数量和训练集样本数量一致为m，但是两者内容不同。若对m个样本的训练集进行T次的随机采样，会得到T个采样数据集且由于随机性，T个采样集都不相同。

Q：在自助法的采样过程中，对m个样本进行m次自助采样，当m趋于无穷大时，最终有多少数据未被选择过？
对于一个样本，它在某一次含 $m$ 个样本的训练集的随机采样中，每次被采集到的概率是 $\frac{1}{m}$。不被采集到的概率为 $1-\frac{1}{m}$。如果$m$次采样都没有被采集中的概率是 $(1-\frac{1}{m}{)}^m$。当$m\to \infty$时， $(1-\frac{1}{m}{)}^m\to \frac{1}{e}\simeq 0.368$。也就是说，在bagging的每轮随机采样中，训练集中大约有 $36.8\%$ 的数据没有被采样集采集中。

袋外数据（Out of Bag，OOB）,即对于这部分大约36.8%的没有被采样到的数据。这些数据可用作测试，用来检测模型的泛化能力。

由于Bagging算法每次都进行采样来训练模型，因此泛化能力很强，对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些，也就是模型的偏倚会大一些。

注意：这和GBDT的子采样是不同的。GBDT的子采样是无放回采样。

2、弱分类器和结合决策

弱学习器：没有限制，最常用的一般也是决策树和神经网络。

对于分类问题，bagging通常采用简单投票法，将最多票数的类别或者类别之一作为最终模型的输出。

对于分类问题，bagging通常采用简单平均法，将T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。

二、Bagging算法流程

伪代码
输入：样本集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$，弱分类器算法，弱分类器迭代次数 T。
输出：最终强分类器 $f(x)$

1. 对于 $t=1,2,...,T$：
   a） 对训练集进行第 $t$ 次随机采样，共采样 $m$ 次，得到包含 $m$ 个样本的采样集 $D_t$。
   b）用采样集 $D_t$ 训练第 $t$ 个弱分类器 $G_t(x)$
2. 若是分类算法预测，则T个弱学习器投出最多票数的类别或者类别之一为最终类别。若是回归算法，T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。

三、随机森林（Random Forest，RF）

随机森林(Random Forest，RF) 是 Bagging 算法的进化版，其思想仍是bagging。

1、特点

优点

• 训练可以高度并行化，提升大样本的训练速度；
• 具有极好的准确率；
• 能够有效地运行在大数据集上；
• 能够处理具有高维特征的输入样本，而且不需要降维；
• 能够评估各个特征在分类问题上的重要性；
• 在生成过程中，能够获取到内部生成误差的一种无偏估计；
• 对于缺省值问题也能够获得很好得结果。

缺点

• 在某些噪音比较大的样本集上，RF模型容易陷入过拟合。
• 取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。

2、两个“随机”

每棵树的按照如下规则生成如下：

（1） 若训练集大小为 $N$，对于每棵树而言，随机且有放回地从训练集中的抽取 $N$ 个训练样本（ $bootstrapsample$ 方法），作为该树的训练集；(每棵树的训练集都是不同的，而且里面包含重复的训练样本)
Q1：为什么要随机抽样训练集？
A1：若不进行随机抽样，每棵树的训练集都一样，则最终训练出的树分类结果也是完全一样的，这样的话完全没有bagging的必要；
Q2：为什么要有放回地抽样？
如是无放回采样，则每棵树的训练样本是不同的，没有交集，则每棵树都是"有偏的"，都是绝对"片面的"（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决，这种表决应该是"求同"，因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的，这样无异于是"盲人摸象"。

（2） 如果每个样本的特征维度为 $M$，指定一个常数 $m<<M$，随机地从 $M$ 个特征中选取 $m$ 个特征子集 ，每次树进行分裂时，从这 $m$ 个特征中选择最优的；

（3） 每棵树都尽最大程度的生长，并且没有剪枝过程。

两个随机性的引入对随机森林的分类性能至关重要。它们使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力（比如：对缺省值不敏感）。

3、分析

随机森林分类效果（错误率）与两个因素有关：

• 森林中任意两棵树的相关性：相关性越大，错误率越大；
• 森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低。

==》
减小特征选择个数m，树的相关性和分类能力也会相应的降低；增大m，两者也会随之增大。所以关键问题是如何选择最优的m（或者是范围），这也是随机森林唯一的一个参数。

4、袋外错误率（oob error）

在构建每棵树时，我们对训练集使用了不同的bootstrap sample（随机且有放回地抽取）。所以对于每棵树而言（假设对于第k棵树），大约有 $36.8\%$ 的训练实例没有参与第 $k$ 棵树的生成，它们称为第k棵树的oob样本。

依据计算袋外错误率oob error（out-of-bag error），可以选择最优的 $m$。

oob 估计(以样本为单位)：

• 对每个样本，计算它作为oob样本的树对它的分类情况；
• 多数投票作为该样本的分类结果；
• 用误分个数占样本总数的比率作为随机森林的oob误分率。

oob错误率是随机森林泛化误差的一个无偏估计，它的结果近似于需要大量计算的k折交叉验证。

四、RF实例

1、API

在scikit-learn中，RandomForest的分类类是RandomForestClassifier，回归类是RandomForestRegressor，需要调参的参数包括两部分，第一部分是Bagging框架的参数，第二部分是CART决策树的参数。

• 官方文档 sklearn.ensemble.RandomForestClassifier
• 官方文档 sklearn.ensemble.RandomForestRegressor

class sklearn.ensemble.RandomForestClassifier(n_estimators=’warn’, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None)[source]

关键部分参数

• n_estimators： 弱学习器的最大迭代次数，或者说最大的弱学习器的个数，默认是10。一般来说n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合，一般选择一个适中的数值。实际应用中，可以以10为单位，考察取值范围在1至201的调参情况。
• bootstrap：默认True，是否有放回的采样。
• oob_score：默认False，即是否采用袋外样本来评估模型的好坏。个人推荐设置为True，因为袋外分数反应了一个模型拟合后的泛化能力。对单个模型的参数训练，虽然可用cross validation来进行，但特别消耗时间，且对于随机森林也没有大的必要，所以用oob数据对决策树模型进行验证，算是一个简单的交叉验证，性能消耗小，但是效果不错。
• criterion：CART树做划分时对特征的评价标准，分类模型和回归模型的损失函数是不一样的。分类RF对应的CART分类树默认是基尼系数gini,另一个可选择的标准是信息增益entropy，是用来选择节点的最优特征和切分点的两个准则。回归RF对应的CART回归树默认是均方差mse，另一个可以选择的标准是绝对值差mae。一般来说选择默认的标准就已经很好的。
• max_features: RF划分时考虑的最大特征数。默认是None,意味着划分时考虑所有的特征数；如果是log2意味着划分时最多考虑$lo{g}_{2}N$个特征；如果是sqrt或者`auto意味着划分时最多考虑 N~√N个特征。如果是整数，代表考虑的特征绝对数。如果是浮点数，代表考虑特征百分比，即考虑（$百分比\times N$）取整后的特征数，其中$N$为样本总特征数。一般来说，如果样本特征数不多，比如小于50，我们用默认的"None"就可以了，如果特征数非常多，我们可以灵活使用刚才描述的其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。
• max_depth: 决策树最大深度。默认为None，决策树在建立子树的时候不会限制子树的深度这样建树时，会使每一个叶节点只有一个类别，或是达到min_samples_split。一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。
• min_samples_split: 内部节点再划分所需最小样本数，默认2。这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。 默认是2, 如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。
• min_samples_leaf：叶子节点最少样本数。 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。 默认是1,可以输入最少的样本数的整数，或者最少样本数占样本总数的百分比。如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。

RF重要的框架参数比较少，主要需要关注的是 n_estimators，即RF最大的决策树个数；
上面决策树参数中最重要的包括最大特征数max_features， 最大深度max_depth， 内部节点再划分所需最小样本数min_samples_split和叶子节点最少样本数min_samples_leaf。

进行预测的几种常用方法

• predict_proba(x)：给出带有概率值的结果。每个点在所有label（类别）的概率和为1.
• predict(x)：直接给出预测结果。内部还是调用的predict_proba()，根据概率的结果看哪个类型的预测值最高就是哪个类型。
• predict_log_proba(x)：和predict_proba基本上一样，只是把结果给做了log()处理。

2、示例

（１）特征选择

wine数据：下载链接

# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

DATA_PATH = './data/wine.data'
data = pd.read_csv(DATA_PATH, header=None)
data.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
				'Alcalinity of ash', 'Magnesium', 'Total phenols',
				'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
				'Color intensity', 'Hue', 'OD280/OD315 of diluted wines', 'Proline']
# print(data)

# 查看标签信息
class_label = np.unique(data['Class label'])
# print(class_label)
# 查看数据信息
# info_data = data.info()
# print(info_data)

# 除去标签之外，共有13个特征，数据集的大小为178，
# 下面将数据集分为训练集和测试集
X, y = data.iloc[:, 1:].values, data.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=2019)
# 获取特征名称
feat_labels = data.columns[1:]
print(feat_labels)

# n_estimators：森林中树的数量
# n_jobs 整数可选（默认=1）适合和预测并行运行的作业数，
# 如果为-1，则将作业数设置为核心数
forest = RandomForestClassifier(n_estimators=10000, random_state=2019, n_jobs=-1)
forest.fit(X_train, y_train)

# 下面对训练好的随机森林，完成重要性评估
# feature_importances_  可以调取关于特征重要程度
importances = forest.feature_importances_
print("重要性：", importances)

X_columns = data.columns[1:]
indices = np.argsort(importances)[::-1] 
for f in range(X_train.shape[1]):
	print("%2d) %-*s %f" % (f+1, 30, feat_labels[indices[f]], importances[indices[f]]))

# 筛选变量（选择重要性比较高的变量）
threshold = 0.15
x_selected = X_train[:, importances > threshold]

# 可视化
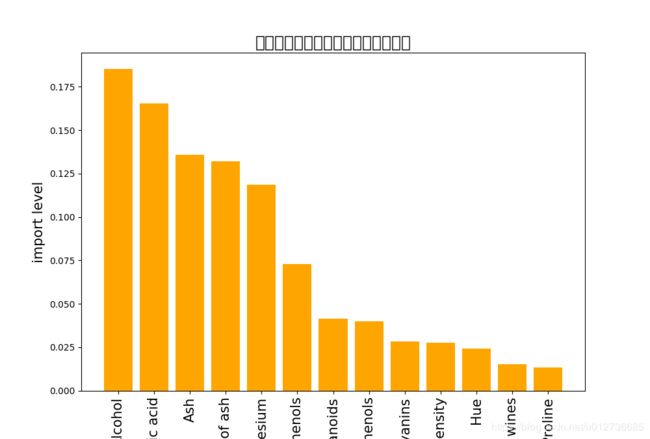
plt.figure(figsize=(10, 6))
plt.title("红酒的数据集中各个特征的重要程度", fontsize=18)
plt.ylabel("import level", fontsize=15, rotation=90)
plt.rcParams['font.sans-serif'] = ["SimHei"]
plt.rcParams['axes.unicode_minus'] = False
for i in range(X_columns.shape[0]):
	plt.bar(i,importances[indices[i]],color='orange',align='center')
	plt.xticks(np.arange(X_columns.shape[0]),X_columns,rotation=90,fontsize=15)
plt.show()

输出结果

重要性： [0.12039608 0.03059304 0.01423496 0.02537548 0.0393332  0.04570302
 0.13610644 0.01406945 0.02534866 0.16986098 0.07455494 0.12314857
 0.18127517]
 
 1) Proline                        0.181275
 2) Color intensity                0.169861
 3) Flavanoids                     0.136106
 4) OD280/OD315 of diluted wines   0.123149
 5) Alcohol                        0.120396
 6) Hue                            0.074555
 7) Total phenols                  0.045703
 8) Magnesium                      0.039333
 9) Malic acid                     0.030593
10) Alcalinity of ash              0.025375
11) Proanthocyanins                0.025349
12) Ash                            0.014235
13) Nonflavanoid phenols           0.014069

（２）oob错误率

import matplotlib.pyplot as plt

from collections import OrderedDict
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier

print(__doc__)

RANDOM_STATE = 2019

# Generate a binary classification dataset.
X, y = make_classification(n_samples=500, n_features=25,
                           n_clusters_per_class=1, n_informative=15,
                           random_state=RANDOM_STATE)

# NOTE: Setting the `warm_start` construction parameter to `True` disables
# support for parallelized ensembles but is necessary for tracking the OOB
# error trajectory during training.
ensemble_clfs = [
    ("RandomForestClassifier, max_features='sqrt'",
        RandomForestClassifier(n_estimators=100,
                               warm_start=True, oob_score=True,
                               max_features="sqrt",
                               random_state=RANDOM_STATE)),
    ("RandomForestClassifier, max_features='log2'",
        RandomForestClassifier(n_estimators=100,
                               warm_start=True, max_features='log2',
                               oob_score=True,
                               random_state=RANDOM_STATE)),
    ("RandomForestClassifier, max_features=None",
        RandomForestClassifier(n_estimators=100,
                               warm_start=True, max_features=None,
                               oob_score=True,
                               random_state=RANDOM_STATE))
]

# Map a classifier name to a list of (, ) pairs.
error_rate = OrderedDict((label, []) for label, _ in ensemble_clfs)

# Range of `n_estimators` values to explore.
min_estimators = 15
max_estimators = 175

for label, clf in ensemble_clfs:
    for i in range(min_estimators, max_estimators + 1):
        clf.set_params(n_estimators=i)
        clf.fit(X, y)

        # Record the OOB error for each `n_estimators=i` setting.
        oob_error = 1 - clf.oob_score_
        error_rate[label].append((i, oob_error))

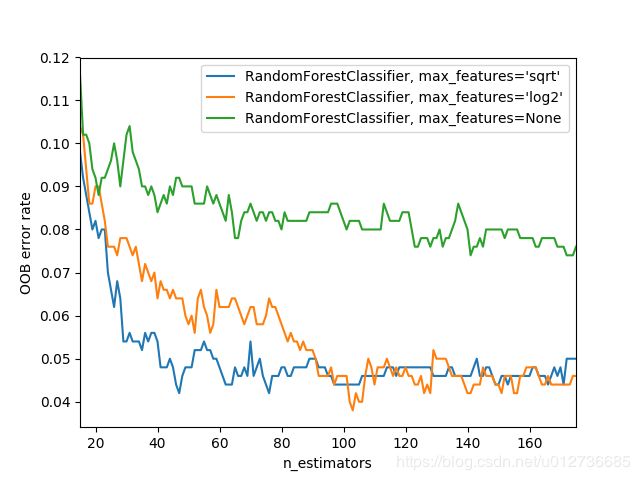
# Generate the "OOB error rate" vs. "n_estimators" plot.
for label, clf_err in error_rate.items():
    xs, ys = zip(*clf_err)
    plt.plot(xs, ys, label=label)

plt.xlim(min_estimators, max_estimators)
plt.xlabel("n_estimators")
plt.ylabel("OOB error rate")
plt.legend(loc="upper right")
plt.show()

输出结果

五、RF的推广

基于RF的变种算法，广泛应用在分类回归、特征转换、异常点检测等场景。

1、extra trees

与Random Forest区别：

• 对于每个决策树的训练集，RF采用的是随机采样bootstrap来选择采样集作为每个决策树的训练集，而extra trees一般不采用随机采样，即每个决策树采用原始训练集。
• 在选定了划分特征后，RF的决策树会基于基尼系数，均方差之类的原则，选择一个最优的特征值划分点，这和传统的决策树相同。但是extra trees比较的激进，它会随机的选择一个特征值来划分决策树。

从第二点可以看出，由于随机选择了特征值的划分点位，而不是最优点位，这样会导致生成的决策树的规模一般会大于RF所生成的决策树。也就是说，模型的方差相对于RF进一步减少，但是偏倚相对于RF进一步增大。在某些时候，extra trees的泛化能力比RF更好。

2、Totally Random Trees Embedding

Totally Random Trees Embedding(TRTE)是一种非监督学习的数据转化方法。它将低维的数据集映射到高维，从而让映射到高维的数据更好的运用于分类回归模型。

TRTE在数据转化的过程也使用了类似于RF的方法，建立T个决策树来拟合数据。当决策树建立完毕以后，数据集里的每个数据在T个决策树中叶子节点的位置也定下来了。比如我们有3颗决策树，每个决策树有5个叶子节点，某个数据特征x划分到第一个决策树的第2个叶子节点，第二个决策树的第3个叶子节点，第三个决策树的第5个叶子节点。则x映射后的特征编码为(0,1,0,0,0, 0,0,1,0,0, 0,0,0,0,1), 有15维的高维特征。这里特征维度之间加上空格是为了强调三颗决策树各自的子编码。

3、Isolation Forest

Isolation Forest（IForest）是一种异常点检测的方法。

• 对于在T个决策树的样本集，IForest也会对训练集进行随机采样，但是采样个数要远远小于训练集个数（目的是异常点检测，只需要部分的样本，一般就可以检测出异常点）。
• 对于每一个决策树的建立，IForest采用随机选择一个划分特征，对划分特征随机选择一个划分阈值。
• IForest一般会选择一个比较小的最大决策树深度max_depth,原因同样本采集，用少量的异常点检测一般不需要这么大规模的决策树。

异常点判断：将测试样本点 $x$ 拟合到 $T$ 颗决策树。计算在每颗决策树上该样本的叶子节点的深度 $h_t(x)$。从而可以计算出平均高度 $h(x)$。此时我们用下面的公式计算样本点$x$的异常概率:
$$s(x,m)=2^{-\frac{h(x)}{c(m)}}$$
其中，$m$为样本个数。$c(m)$的表达式为：
$$c(m)=2\ln (m-1)+\xi -2\frac{m-1}{m},\xi \text{为欧拉常数}$$
$s(x,m)$的取值范围是$[0,1]$，取值越接近于1，则是异常点的概率也越大。

参考资料

• Sklearn-RandomForest随机森林
• Bagging与随机森林算法原理小结