导航动态避让算法RVO的优化ORCA(Optimal Reciprocal Collision Avoidance)

来源于文档的主要内容：
ORCA主页
文档来源
本文要解决的问题：
$n(n>0)$个个体导航向目标点移动过程中，对于其它个体或者障碍物进行动态避让，并寻找最佳路径向目标点移动。

和A星寻路算法有什么异同？
相对而言，
ORCA是局部导航，导航目标是在个体自己的周围，让个体自身避开与自己接近的其它个体目标和障碍，ORCA只能感知到靠近自身周围的情况，没有全局环境的信息，所以它只管导航时不与自己周围其它个体目标和障碍避免碰撞，或者说重叠在一起，却不能为自身起点和目标点之间找到最短路径，这刚好是A*星寻路解决的问题。
A星寻路算法刚好和ORCA形成互补：
A星是全局寻路算法，会根据配置最大可能的保证找到导航个体自身起点到目标点的最短路径，算法的全局信息中有着整个环境的障碍信息。但A星没有感知所有导航个体的具体状态和周围的“交通状况”信息，所以A星算法不处理可能会碰撞问题，因此多个导航个体之间可能会重叠在一起。这刚好是ORCA解决的问题。
所以可以把它们结合起来，形成互补，Unity有个插件A星 Pathfinding Project Pro就是将两者结合起来了，形成动态避让的全局导航。

我们在本文中讨论的问题正式定义如下：
在一个共享的空间环境下有$n(n>0)$个机器人，为了简单起见，我们假设机器人都是圆形，空间环境则为2D空间。（这样我们在此中更容易提出定义和算法，也能适用于多维）。每个机器人$A$都有一个当前位置$p_A$(圆盘的中心点)、当前速度$v_A$和半径$r_A$，这些参数都是机器人的外在状态，它们可以被其他机器人观察到。此外，当每个机器人往目标点方向的路上没有其它机器人阻挡时，都有最大速度 $v_A^{max}$ 和期望速度 $v_A^{pref}$（$v_A^{pref}$直接指向目标点，它的长度等于$v_A^{max}$），但这些事机器人的内部参数，无法被其它机器人观察到。
解决方案：
我们提出了一个严格的方案，假设有$n$个个体，他们之间使用相同的避免碰撞策略，提供充足条件下，他们相互在$t$时间内避免碰撞的方案。
这个方案基于速度，这意味着每个机器人都会考虑到其它机器人的速度避免与他们碰撞，然后从他自己的可选速度空间区域中选择自己的新速度，其它被标为"禁止"的区域则被其它机器人占据。对于每个其它机器人，当前机器人都有一个半平面(速度空间)的可选速度，用来与其它机器人避免碰撞。那么当前机器人可以从这些可选的多个平面的交集中选择一个最佳的速度，这个可以通过线性划分有效的完成。线性划分在机器人密集的环境下可能不可行，在这种情况下，我们通过三维空间来选择“尽可能安全”的速度。
我们要做的是：
第一，为每个机器人A同步独立地为它们自己选择一个新的速度 $v_A^{new}$，并且这个新速度 $v_A^{new}$ 能够保证在预定的t时间内，持续的与别的机器人无碰撞移动。
第二，每个机器人选择新速度 $v_A^{new}$时，都要尽可能的接近它们自己的期望速度$v_A^{pref}$。
第三，每个机器人之间不允许进行沟通，所以它们只能够观察得到别的机器人的当前位置和当前速度。然而，每个机器人可以假设其它机器人也是使用和自己一样的策略来选择新的速度 $v_A^{new}$。
这个问题无法使用中心协调的方式解决，因为每个机器人的期望速度只有它们自己知道。
第四节，我们描述为机器人选择时间t内避免碰撞的新速度准备了足够多的条件。
第五节，展示了如何使用此原理循环多个机器人导航。

所以，整篇文章主要部分要解释的动态避让效果也就如下图所示：
也就是要达成如下效果图这般动态避让导航的样子，走位四不四很风骚？ ^ ^。

图解：
以红色圆为主角，我们假设他叫$A$，其它颜色的圆各叫$BCDEF$等。
图中各种颜色的直线就是上述的平面的分割线，分给A的半平面下文称为$ORC{A}_{A|B}^t$。白色区域是$A$避开多个其它颜色圆的多个半平面的交集区域，也就是自己的可选速度范围，下文称为$ORC{A}_A^t$(白色区域图中)。左边黑色点位置是目的地点，主角$A$的期望速度$v_A^{pref}$(图中灰色线段)总是指向它，毕竟那是自己要去的地方嘛。而主角$A$的当前速度 $v_A^{opt}$(图中黑色线段)也想指向它，却无奈被限制在白色区域里，但它不死心，所以它每在下一步选择新速度$v_A^{new}$(图中的黑色线段的下一步状态)都会尽可能的向灰色速度靠近，直到到达目的地。由此，风骚走位图形成

4.1准备
有两个机器人$A$和$B$，障碍速度集合为$V{O}_{A|B}^t$（解释为：A在此集合中选择此速度时，将在时间$t$内与$B$发生碰撞)。
设$D$为以$p$为圆心，$r$为半径的圆：

$D$($p$,$r$) = {$q$| ||q−p|| < $$r$}

那么：

$V{O}_{A|B}^t$ = {$v$|∃$t$ $\in$ [$0$,$\tau$] :: $tv$ $\in$ $D$($p_B$ −$p_A$, $r_A$ + $r_B$)}

有：
（a）两个机器人A和B
（b）这里是速度空间坐标系，障碍速度集合 $V{O}_{A|B}^t$ 几何解释为（灰色区域）形成一个截头的圆锥形，顶点位于原点o（速度空间），它的两边与$r_A$ + $r_B$相切，两边居中为$p_B$ −$p_A$方向上。圆锥的半径由t决定，这里的障碍速度t=2。
（c）避免碰撞向量集合$C{A}_{A|B}^t$ ：避免发生碰撞情况下，$B$的选择速度集合为$V_B$(深灰色)，这里为坐标系的第四象限，也就是说明$B$的速度集合方向为向右下，那么给$A$的选择的速度集合$C{A}_{A|B}^t$也就是 $V{O}_{A|B}^t$的Minkowski sum的补集。
（PS : 临阵磨枪，脑补一下)Minkowski sum的大概定义如下：
设$X$⊕$Y$表示为X和Y的Minkowski sum，绿色为$X$蓝色为$Y$，红色为和：
$X$ ⊕$Y$ = {$x$+$y$|$x$ $\in$ $X$, $y$ $\in$ $Y$},

障碍速度的几何解释如(b)所示，记住：$C{A}_{A|B}^t$和 $C{A}_{B|A}^t$相对于原点是对称的。
设$v_A$和$v_B$分别为机器人$A$和$B$的当前速度，根据障碍速度的定义意味着，如果$v_A$− $v_B$$\in$ $V{O}_{A|B}^t$，那么$A$和$B$持续以当前速度移动将在时间$t$ 内碰撞。相反，如果$v_A$− $v_B$ $\notin$ $V{O}_{A|B}^t$那么$A$和$B$在$t$ 时间内不会碰撞。

那么对应任何$v_B$，如果$v_B$$\in$ $V_B$和$v_A$$\notin$ $V{O}_{A|B}^t$ ⊕$V_B$，那么$A$和$B$以当前速度在$t$时间内是保证不会碰撞的，从而推导出避免碰撞速度集合$C{A}_{A|B}^t$($V_B$)，也就是在$B$选择$v_B$速度后$A$能够选择的速度集合。见图©：

$C{A}_{A|B}^t$($V_B$) = {$v$|$v$$\notin$ $V{O}_{A|B}^t$ ⊕$V_B$} （图c公式）

对于$A$和$B$的速度集合$V_A$和$V_B$，如果$V_A$$\subseteq$$C{A}_{A|B}^t$($V_B$) 和 $V_B$$\subseteq$$C{A}_{B|A}^t$($V_A$) ，那么，$A$和$B$相互不碰撞。
如果$V_A$=$C{A}_{A|B}^t$($V_B$) 和 $V_B$=$C{A}_{B|A}^t$($V_A$) ，那么，我们称$V_A$和$V_B$互为最大化。

4.2
因为$A$和$B$是相对独立的机器人，所以它们应该在没有沟通的情况下，推断出自己被允许的速度范围，这里有无数对的$V_A$和$V_B$在遵循着这些要求。但在这些成对的$V_A$和$V_B$中，在他们互为最大化的可选的避免碰撞速度集合中选择一对接近最优的速度，称$A$的为$v_A^{opt}$，$B$的为$v_B^{opt}$。( opt : optimization)
我们称以上这些避免碰撞可选范围$A$和$B$相互最大化的速度集合$A$的为$ORC{A}_{A|B}^t$，$B$的为$ORC{A}_{B|A}^t$。

$ORCA$的具体描述
定义 1 (Optimal Reciprocal Collision Avoidance)
机器人A的$ORC{A}_{A|B}^t$，机器人B的为$ORC{A}_{B|A}^t$的定义是，两边A和B避免碰撞，并且他们可选新速度范围互为最大化，以下用等式描述：

$C{A}_{A|B}^t$($ORC{A}_{B|A}^t$) = $ORC{A}_{A|B}^t$ 和 $C{A}_{B|A}^t$($ORC{A}_{A|B}^t$) = $ORC{A}_{B|A}^t$

即以上等式解释为在时间$t$内避免与机器人$B$的$ORC{A}_{B|A}^t$碰撞的向量区域，就是的机器人A的$ORC{A}_{A|B}^t$，反则反之。
那么有，

|$ORC{A}_{A|B}^t$$\bigcap$$D$($v_A^{opt}$,$r$)| = |$ORC{A}_{B|A}^t$$\bigcap$$D$($v_B^{opt}$,$r$)| $\ge$ min(|$V_A$,$D$($v_A^{opt}$,$r$)|,|$V_B$,$D$($v_B^{opt}$,$r$)|)

这意味着$ORC{A}_{A|B}^t$和$ORC{A}_{B|A}^t$包含着更多速度接近$v_A^{opt}$和$v_B^{opt}$，超过任何其它成对的速度的互相避免碰撞速度集合。它们允许选择的速度分布是均匀的，接近最优速度的速度集合数量$A$和$B$的相等。

我们构建$ORC{A}_{A|B}^t$和$ORC{A}_{B|A}^t$的几何图如下

假设$A$和$B$最优速度分别为$v_A^{opt}$和$v_B^{opt}$,假设$A$和$B$一定会碰撞上，即$v_A^{opt}$-$v_B^{opt}$$\in$$V{O}_{A|B}^t$ 。
设$u$是以$v_A^{opt}$- $v_B^{opt}$ 为起点，指向和到以$V{O}_{A|B}^t$边界最近的点为终点的向量：
$u$ = ($argmin$$||$$v$−($v_A^{opt}$−$v_A^{opt}$)$||$)−($v_A^{opt}$−$v_A^{opt}$))，$v$$\in$$\partial V{O}_{A|B}^t$
$\partial 偏导符号$

设n是$\partial V{O}_{A|B}^t$范围内向，以($v_A^{opt}$−$v_B^{opt}$)+$u$为起点向外的法线，那么$u$是对于$A$和$B$在时间$t$内避免碰撞速度需要改变最小的值。为了避免碰撞，机器人以公平的方式"分担责任"，机器应该适配自己的速度为$1/2u$。
（我们引入这些$vopt$(优化速度)来概括$ORCA$的定义。实际上，这些$vopt$等于当前的速度，机器人必须偏离当前轨道来避免可能的碰撞，更多选择在5.2节讨论）

如图：

$Fig.2$
$A$的$ORC{A}_{A|B}^t$跟B避免碰撞的向量集合是一个半平面，被垂直于向量$u$且经过点$v_A^{opt}$+$1/2u$的线分割。
$u$是以$v_A^{opt}$- $v_B^{opt}$ 为起点，指向和到以$V{O}_{A|B}^t$边界最近的点为终点的向量。
$n$是$V{O}_{A|B}^t$范围内向，以($v_A^{opt}$- $v_B^{opt}$)+$u$为起点方向向外的法线。

$ORC{A}_{A|B}^t$允许A的避免碰撞速度集合是以$v_A^{opt}$+$1/2u$为起点，以$n$为方向的半平面；$B$的允许速度集合同理。
$ORC{A}_{A|B}^t$ = {$v$$|$($v$−($v_A^{opt}$ +$1/2u$))· $n$ ≥ $0$}.
以上等式在可能不会碰撞时也有效，即$v_A^{opt}$−$v_B^{opt}$$\notin$$V{O}_{A|B}^t$时。
以上说明每个机器人之间不通过沟通就能观察到彼此之间的大概位置、半径和速度。
这种情况下两个机器人个承担一半保持无碰撞的责任。

5 n个个体避免碰撞
在本节中，我们将展示如何应用上面定义的ORCA原理来实现多个移动机器人之间的n体碰撞避免，并讨论如何在这个框架中加入静态障碍。

10. Mermaid 流程图

感知其它机器人的位置和速度

计算机器人彼此之间的ORCA

使用线性划分选择新的速度

将速度应用于更新机器人位置

$Fig.3$
每个机器人的感知和反应循环示意图

$5.1$基本方案
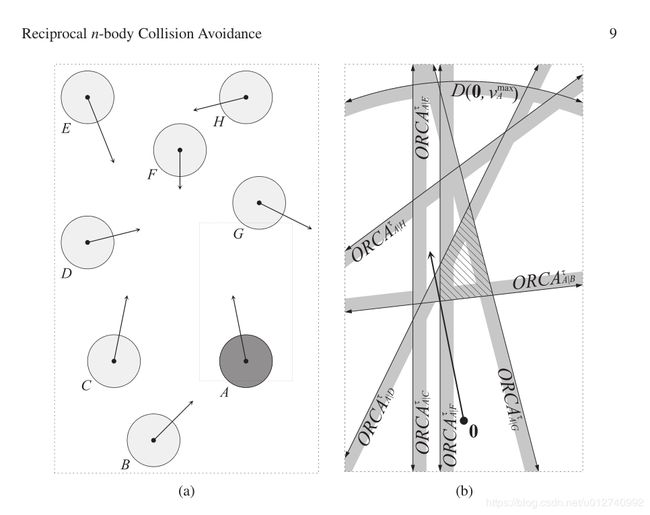
每个机器人$A$在时间$t$内执行连续循环的感知和做反应。 在每次循环中，机器人需要知道自己的和其它机器人的半径、当前位置和当前速度，基于这些信息，机器人$A$推断出自己的对于机器人$B$的$ORC{A}_{A|B}^t$半平面。在这个半平面内允许的速度范围内，$A$又和其它机器人产生半平面，如此之间不断影响，我们定义此为$ORC{A}_A^t$，(见$Fig.4$)
$ORC{A}_A^t$ = $D$$($$0$$,$$v_A^{max}$$)$$\bigcap$$ORC{A}_{A|B}^t$ 其中 $($$B$$̸=$$A$$)$ （7）
请注意，此定义还包括机器人A的最大速度限制。
接下来，避免碰撞允许速度范围内所有的速度，机器人选择一个最接近它的期望速度$v_A^{pref}$的新速度$v_A^{new}$：
$v_A^{new}$= $argmin||v-$$v_A^{pref}$$||，v\in$$ORC{A}_A^t$（8）
我们将在下面展示如何计算这个实际应用的新速度。 更新机器人
达到新的位置；
$p_A^{new}$= $p_A^{}$ +$v_A^{new}$$∆t$ , （9）
所有的感知-反应都是（7）（8）（9）这个循环过程。
上述过程中的关键步骤是计算新的速度$v_A^{new}$,也就是（7）和（8）的定义。这可以使我们有效的使用线性规划算法完成，如$ORC{A}_A^t$是受多个机器人影响产生多个半平面共同内由线性规划约束引起的交集区域，见下图$Fig.4$。最优的解就是此区域速度集合中的某个速度到期望速度$v_A^{pref}$的距离，甚至这是个二次最优函数也不影响线性规划算法的特性，因为它只有一个局部最小值。
我们使用[3]的有效算法，它逐个添加约束
随机顺序，同时跟踪当前最佳新速度

$Fig.4$
(a)8个机器人的，它们各自的速度用箭头表示。
(b)A的受多个机器人影响的多个半平面$t=2$和$v_{\ast }^{opt}$=$v_{\ast }^{}$)。$E$和$C$的半平面重合，虚线区域是$A$的多个半平面交集区域，也就是避免碰撞被允许的新速度选择区域范围。

算法目的是在$ORC{A}_A^t$中找到最接近$v_A^{pref}$的新速度$v_A^{new}$，如果线性规划算法不可行，即$ORC{A}_A^t$ $=0$.，那么返回失败。$v_A^{max}$的调整不会影响算法的运行。

如果谨慎选择机器人的优化速度（我们将在5.2节讨论），ORCAτA将不会是空的，因此，总有一种解决方案可以保证机器人在t时间内无碰撞。

我们可以通过不包括所有其他机器人的约束来提高选择速度的效率，仅仅考虑那些“靠近”的机器人。 事实上，机器人B离机器人A的距离远远超过（vmaxA + vmaxB）那么时间t内是不会与机器人发生碰撞，因此在计算机器人A的新速度时可以安全地将它们排除在线性规划算法之外。还有一个小问题是机器人A不知道其他机器人的最高速度，但这可以通过“猜测”来解决，其它机器人的最高速度等于A的自身。
关于附近机器人的约束影响，可以使用kD树来寻找附近的机器人。
图

$Fig.5$
(a)3个机器人$BCD$密集的向机器人$A$移动。
(b)机器人彼此之间的参数$t=2$和$v_{\ast }^{opt}$=$v_{\ast }^{}$，那么区域ORCAtA是空的，所以$t$时间内无法保证没有碰撞。
©机器人彼此之间的参数$t=2$和$v_{\ast }^{opt}$=$0$，那么得出灰色区域是$ORC{A}_A^t$。

5.2选择最优速度
还有一个问题，如何为每个机器人$A$ 选择$v_A^{opt}$。为了让机器人在没有通信的情况下推断出半平面，$v_A^{opt}$必须是可被其它机器人观察得到的。
在这里，我们讨论一些合理的可能性：
$v_A^{opt}$=$0$ 对应所有的机器人$A$：
这就保证了$ORC{A}_A^t$对于机器人A非空。如上所述，那么线性规划算法将最快为所有机器人找到保证时间t内避免碰撞的速度。对应多个机器人B，点0始终位于障碍速度$V{O}_{A|B}^t$之外，因此半平面$ORC{A}_A^t$总是包含最小速度$0$。实际上，这条线界定了$ORC{A}_A^t$垂直于连接$A$和$B$的线。
将优化速度设置为$0$的缺点是机器人的行为看起来不自然，因为它们只考虑了别的机器人的当前位置，而不是它们的速度，在密集的情况下也可能导致全局僵硬，因为机器人的速度彼此非常接近$0$。
$v_A^{opt}$=$v_A^{pref}$ 对应所有的机器人$A$：
期望速度是机器人的内部状态，因此别的机器人无法观察得到。为了能讨论下去，我们假设某种程度上可以推断出其它机器人的期望速度，然后让所有机器人的优化速度等于期望速度，这在低密度条件下运行很好，但随着优化速度的幅度递增，线性规划算法变得越来越不可行。在大多数情况下，无论密度环境如何，期望速度都具有恒定（大）长度，这将导致即使在均匀的密度环境中导航看起来也不自然。
$v_A^{opt}$=$v_A^{}$ 对应所有机器人$A$：
这里的优化速度是以上两种的理想权衡，在低密度环境下选择偏向期望速度，在高密度环境下选择偏向$0$速度，当然，当前速度要被其它机器人观察得到。
尽管如此，在高密度环境下，线性规划算法依然有可能不可行（见$Fig.5(b)$），这种情况下不能保证选择出一个避免碰撞的速度。为此，我们使用3-D线性规划算法为机器人选择“尽可能安全”的速度（我们在5.3节讨论）。
5.3 密集条件环境
对于所有机器人$A$，我们选择$v_A^{opt}$=$v_A^{}$，在机器人密度极高的情况下，可能会$ORC{A}_A^t$为空（见图5(b)），并且5.1的算法返回是不可行的，在这种情况下无法保证有无碰撞速度。
这种情况下，我们为每个机器人选择“尽可能安全”的速度，即速度最低限度的“穿透”其它机器人引起的约束。
正式点的说，就是设 $d_{A|B}^{}(v)$为速度$v$到半平面$ORC{A}_{A|B}^t$的边界的距离。如果$v\in$$ORC{A}_{A|B}^t$，那么$d_{A|B}^{}(v)$为负。我们要选择最小的可行速度，选的也就是速度到多个机器人影响的各个平面的距离中最大的一个。

$v_A^{new}$= $argmin$ $max$ $d_{A|B}^{}(v)$ 其中 $v\in D(0,$$v_A^{max}$$)$$,$$B$$̸=$$A$

几何上，这可以解释为以相同的速度，向外垂直移动半平面$ORC{A}_{A|B}^t$的边缘，直到恰好得到一个有效的速度，这也就是我们要选的最小可行速度。
我们可以使用三维线性规划算法找到这个速度。对于每一个其它机器人$B$，距离函数 $d_{A|B}^{}(v)$在三维$(v,d)$空间中是一个平面。我们通过距离函数来寻找一个点$(v\ast ,d\ast )$，它位于所有的平面之上，找到它的最小值$d$，然后设置$v_A^{new}$$=$$v_{\ast }^{}$。
实际上，我们可以将问题投射到v平面上，这样所有的几何形状操作可以二维进行，三维线性规划算法总是可行的，所以它总是返回一个解决方案。
请注意，在这些密集的情况下，为机器人选择的新速度不会取决于机器人的期望速度。 这意味着机器人’顺其自然流动’，其行为完全由机器人周围的机器人决定。
效果如图：

关于静态障碍：

$Fig.6$
（a）机器人$A$和线段障碍物$O$的配置。
（b）障碍速度的几何形状$V{O}_{A|O}^t$，$t=2$。
（c）半平面切割线$ORC{A}_{A|O}^t$与$V{O}_{A|O}^t$相切于边上到$v_A^{opt}$最近的点，等于0时为碰到障碍$O$。

5.4 静态障碍物
到目前为止，我们只讨论过机器人如何避免相互碰撞，但是
典型的多机器人环境也包含（静态）障碍物。 我们可以很容易地将它们纳入上述框架中。 我们基本上遵循以上相同的方法，一个关键的区别是障碍物不移动，所以机器人应该完全负责避免与他们发生碰撞。

我们通常可以假设障碍物被建模为线段的集合。 设$O$是这样的线段之一，$A$是半径为$r_A^{}$，位于点$p_A^{}$的机器人。那么由$O$影响的障碍速度$V{O}_{A|O}^t$定义如下：
$V{O}_{A|O}^t$ $=$ {v|∃t ∈ [0,τ] :: tv ∈ O⊕ −D($p_A^{}$,$r_A^{}$)}.
如果其速度$v_A^{}$在$V{O}_{A|O}^t$内，则代理$A$将在$\tau$时间内与障碍物$O$碰撞，反之则在t时间内避免碰撞。因此，对应障碍$O$，$A$允许的速度区域为$V{O}_{A|O}^t$的补集。这个补集是一个非凸区域，所以无法使用5.1的划线算法，为此，对于障碍O，我们定义了A可允许的速度集合$ORC{A}_{A|O}^t$的半平面：划分线为为切线过$V{O}_{A|O}^t$边界上一个最接近$v_A^{opt}$的点(见图$Fig.6(c)$)。
图

$Fig.7$
两个机器人的踪迹模拟，机器人显示为彩色磁盘它们的初始位置很轻，随着时间的推移变暗。
（a）两机器人通过彼此的踪迹。
(b)五个机器人去到彼此对面点的踪迹。

如果遇到障碍，对于所有机器人A我们选择$v_A^{opt}$$=0$，$A=0$.这保证了
机器人始终存在有效的速度，以避免在τ时间内与障碍物发生碰撞。 对于障碍物而言，我们通常可以使用比其他机器人更小的τ值，因为机器人需要避开其它机器人的情况下，通常不应该对障碍物“害羞”不敢向障碍物靠近。
另一方面，对于机器人在障碍物上允许的速度的限制不与障碍碰撞很难，应该不惜一切代价避免与障碍物碰撞。
我们注意到避免与障碍碰撞的速度集合半平面只保证机器人不与障碍碰撞，没有让机器人绕开障碍移动，这有可能与期望速度方向相反，也就是非最短路径，这应该用全局寻路导航来处理，例如A*寻路啦。