【数据结构】----平衡二叉树怎么自己画？

【数据结构】平衡二叉树怎么自己画？

      

是什么？

    要了解平衡二叉树，先得了解什么是二叉树？

二叉树定义：

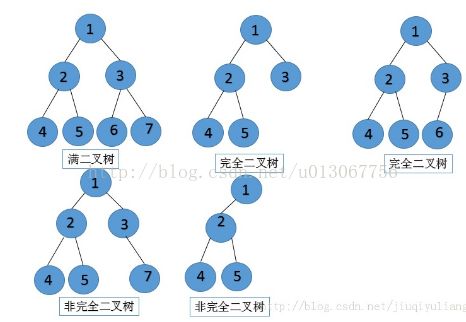
在计算机中，二叉树是每一个节点最多有两个子树的结构。通常子树被称作“左子树（left subtree）”“右子树（right subtree）”. 二叉树常被用于实现二叉树查找和二叉堆。

什么是平衡二叉树：

     平衡二叉树（Balance Binary Tree）是二叉树的一个进化体，是一个引入平衡概念的二叉树。与1962年G.M Adelson-Velsky 和E.M.Landis 发明的，也叫AVL树。 平衡二叉树是对于每一个节点来说，他的左右子树高度差不能超过1， 如果插入或者删除一个节点，使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡的状态。

   

 

平衡二叉树是干什么的？

     平衡二叉树很好的解决了二叉树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(LogN)。但是频繁的旋转是插入和删除牺牲掉O(LogN)左右的时间，不过相对于二叉查找树来说，时间上是稳定了许多。

 

怎么画一棵平衡二叉树树（重点突出）

   今天小编想和大家分享的重点是给你几个数，到底怎么画这课平衡二叉树来？

     原则：

     1.将题目中已给的数，依次按二叉排序树的原理将树画下来（左子树值小于根值，右子数值大于根值，整棵树的左右子树值也满足二叉排序树规则。）

     2，每一次插入一个数值，都必须满足二叉排序树规则且左右子树高度只差不能查过1， 超过1 就要旋转。

怎么旋转呢？

（1）首先找平衡因子，平衡因子看那个值先为-2（那个根左右子树或子树高度差超过1，这个根的平衡因子就为-2并且如果有两个平衡因子-2的，旋转那个靠近插入值那边的那个根）；

（2）在刚刚插入的数值中，在同一分支中连续三个数旋转；注意，是沿着这三个数的中位数旋转，如果中位数不在中间，就将交换将中位数放在中间后进行交互后在旋转。

 

下面我来看看实例：

（1）2010年计算机专业统考的一题关于平衡二叉树

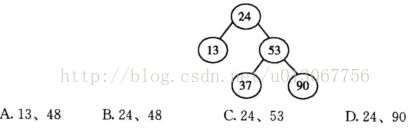
原题：在下图所示的平衡二叉树中，插入关键字48后得到一棵新平衡二叉树，在新平衡二叉树中，关键字37所在节点的左边、右子结点中保存的关键字分别是

  

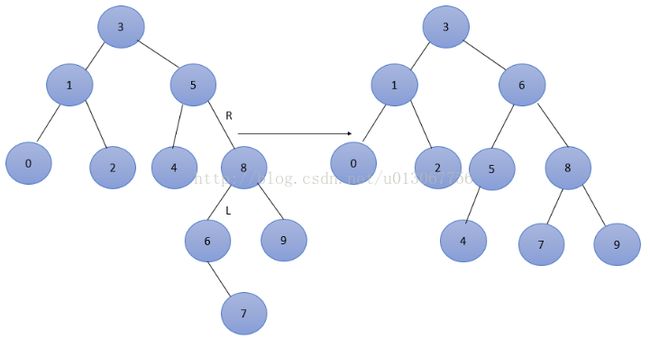
（2）分别为2，1，0，3，4，5，6，9，8，7的10个结点来构造平衡二叉树，构造平衡二叉树过程。

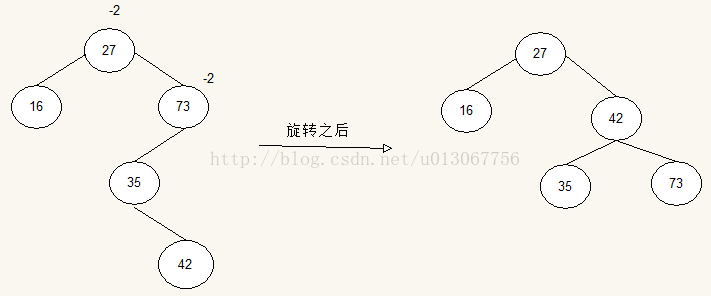
（3）27,16,73,35,42构造平衡二叉树

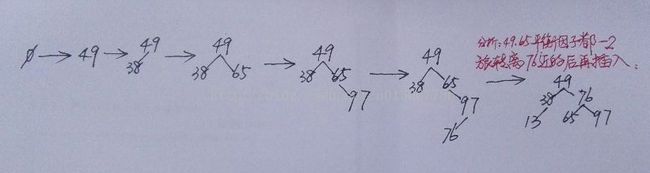
（4）对序列（49,38,65,97,76,13,27,50）构造平很二叉树，并给出构造过程？

 

解答：

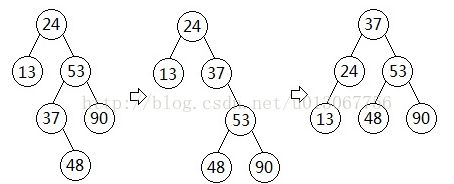
（1）  插入48，按二叉排序树的原理，48插在37的右边，在找平衡因子。

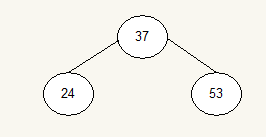
怎么找平衡因子，看哪个根左右子树或子树先出现差大于1，那么这个根平衡因子就为-2，有题目分析，24首先出现平衡因子为-2，所以按照旋转原则来：24,53,37这三个数进行旋转

                      

所以整棵树是这样的:

                 

(2)如果要构造平衡二叉树，第一个必定是空集，注意不能少了空集。

参考文献：

http://blog.csdn.net/wxbmelisky/article/details/47787963

           

（3）如图，现在有两个平衡因子都为-2，所以选择离插入值近的那个，所以是件73,35,42进行旋转；将数值为中位数的放中间进行旋转：

                

（4）平衡二叉树构造过程如下（按二叉排序树的原则一个一个的插入）：

 

 

 

小结：

      学习了二十几年了，考了二十几年了，现在特别特别赞同一句话：

                 

          一点一滴的踏实积累好；基础牢固，前途才能大步！