Name: 贺一珺
Student Number: 2014302290002
Question
3.18 Calculate Poincare section for the pendulum as it undergoes the period-doubling route to chaos. Plot omega versus theta, with one point plotted for each drive cycle, as in Figure 3.9. Do this for F_D =1.4, 1.44 and 1.465, using the other parameters as given in connection in Figure 3.10. You should find that after removing the points corresponding to the initial transient the attractor in the period-1 regime wil contain only a single point. Likewise, if the behavior is period n, the attactor will contain n discrete points.
3.19 Calculate Poincare section for the pendulum but for a frequency with those intrinsic to the system. For example, you might calculate the Poincare sections using an angular frequency omega' that is irrationally related to the driving frequency omega_D (as well as to the natural frequency omega) for your stroboscopic snapshots. Do the results tell you anything about the system?
3.20 Caculate the bifurcation diagram for the pendulum in the vicinity of F_D=1.35 to 1.5. Make a magnified plot of the diagram and obtain the an estimate of the Feignbaum delta parameter.
Abstract
I tried to draw the Poincare section last weed and worked out the plot of attractor. But their are two problems in that homework(I corrected them several days before =w=): the first is that three of those plots are actually in chaos and the plots cannot tell any information about the system; the second question is that the variable dt cannot be devided by integral and that may magnified the error. I corrected those problems in this home work using some tricks and I also bifurcation diagram which made me understand the process to the chaos better. Translation points are also showed directly in this homework. What's more, I tried out vpython and draw 3D model of pendulum using it. There are some difficulties installing it which I 've not solved yet.
Here is a 3D pendulum:
Background
I have give a brief introduction to you about the basic knowledge of chaos. But I have to say that it is far from enough. I will introduce you some interesting concrete topics in chaos.
Strange attractors[1]
Some dynamical systems, like the one-dimensional logistic map defined by x → 4 x (1 – x), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor, since then a large set of initial conditions leads to orbits that converge to this chaotic region.
An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it was not only one of the first, but it is also one of the most complex and as such gives rise to a very interesting pattern, that with a little imagination, looks like the wings of a butterfly.
Unlike fixed-point attractors and limit cycles, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete systems (such as the Hénon map). Other discrete dynamical systems have a repelling structure called a Julia set, which forms at the boundary between basins of attraction of fixed points. Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal structure, and the fractal dimension can be calculated for them.
Iterated function system[1]
IFS fractals, as they are normally called, can be of any number of dimensions, but are commonly computed and drawn in 2D. The fractal is made up of the union of several copies of itself, each copy being transformed by a function (hence "function system"). The canonical example is the Sierpiński gasket, also called the Sierpiński triangle. The functions are normally contractive, which means they bring points closer together and make shapes smaller. Hence, the shape of an IFS fractal is made up of several possibly-overlapping smaller copies of itself, each of which is also made up of copies of itself, ad infinitum. This is the source of its self-similar fractal nature.
Here is an example:
Crutial points
- To solve the problem in last homework, I checked my code and found a mistake: when picking up points that satisfied the peroid condition, I added the phase factors to a wrong place which made the diagrem collapse.
- The first several points make no contribution to curve drawn by static points actually. Thus they can be omitted.
- The peroid of force cannot be devided by time step dt. Thus in every peroid there will be some error. As time goes by, those error will accumulate to a number that should not be neglected. I change the magnitude of the time step dt in this homework to meet the requirement of peroid.
Plotting
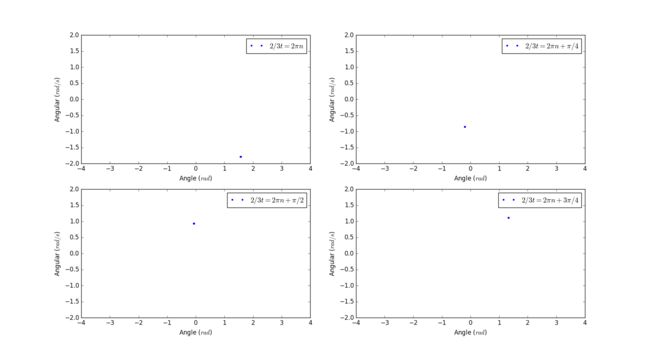
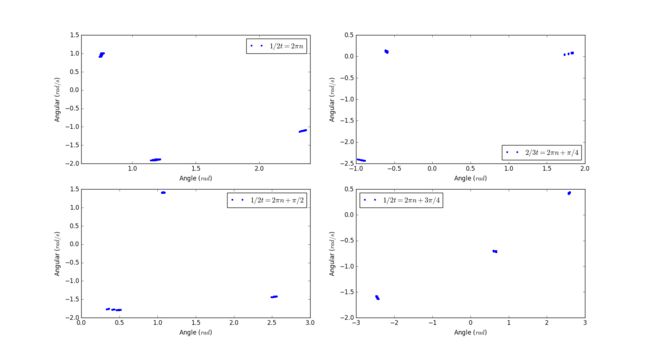
3.18
Here is the code 1
Here is the code 2
Here is the code 3
Initial conditions
Initial angle: 0.2 rad
Initial angular velocity: 0 rad/s
Length of pendulum: 9.8m
Frequency of force: 2/3
Magnitude of force: 1.4
Poincare sections:
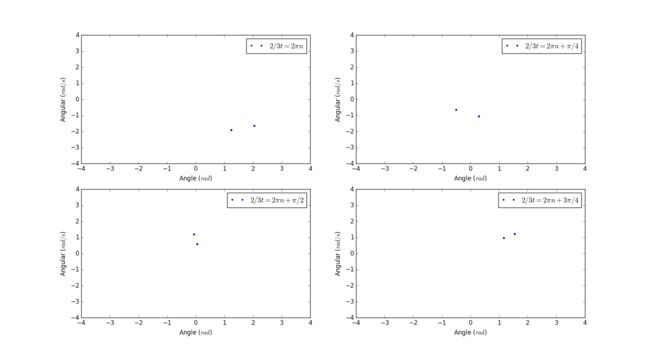
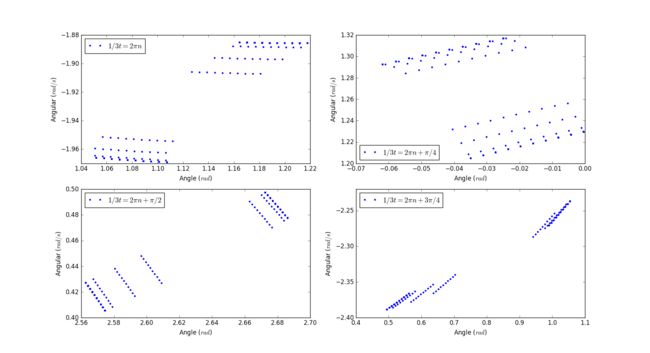
Initial conditions
Initial angle: 0.2 rad
Initial angular velocity: 0 rad/s
Length of pendulum: 9.8m
Frequency of force: 2/3
Magnitude of force: 1.44
Poincare sections:
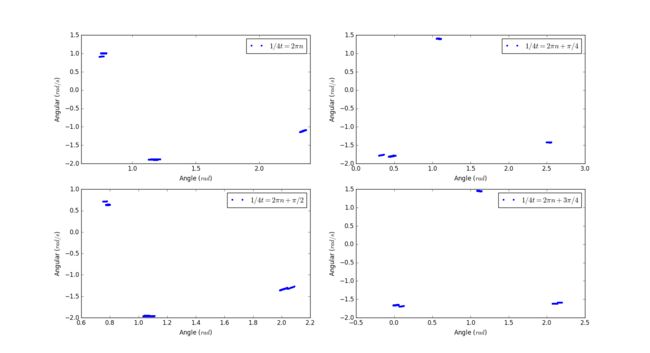
Initial conditions
Initial angle: 0.2 rad
Initial angular velocity: 0 rad/s
Length of pendulum: 9.8m
Frequency of force: 2/3
Magnitude of force: 1.465
Poincare sections:
Conclusion
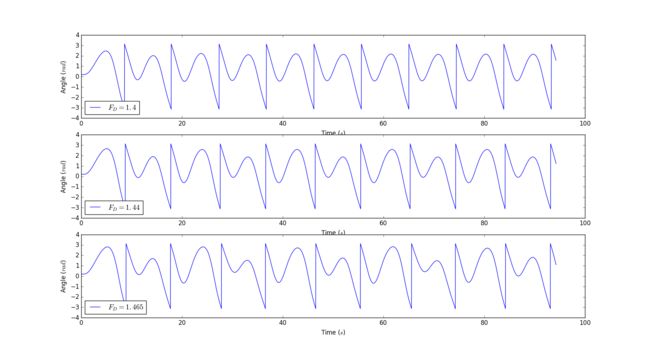
The peroids of pendulums with different magnitude of force are shown directly in this graph:
It can be easily seen that the peroid double as the magnitude of F_D increase, which is coninsident with what are tought in Poincare section.
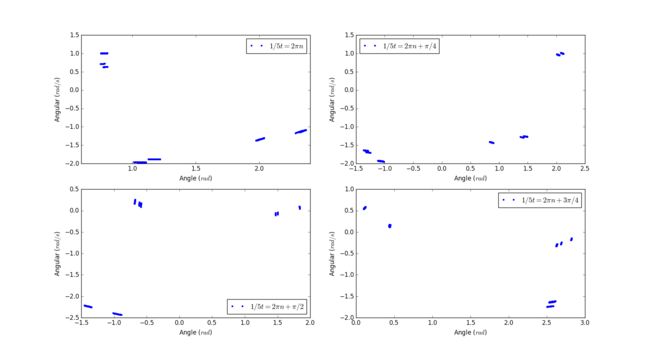
3.19
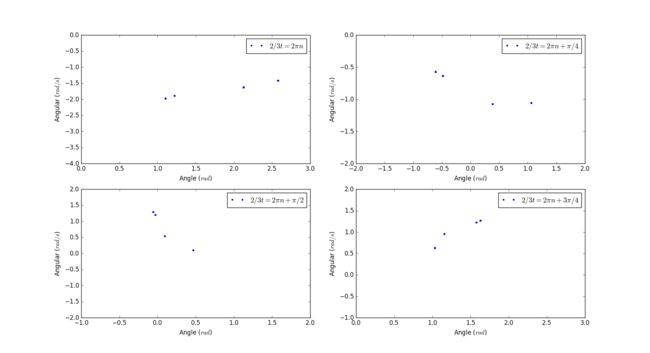
I tried five different number as the peroid of Poincare section, here are results:
Peroid = 2pi
Peroid = 4pi
Peroid = 6pi
Peroid = 8pi
Peroid = 10pi
Conclusion
In this problem we use various peroids which differ from that of force. I found that when the peroid we choose have nothing to do with the peroid of force, no regularity can be worked out except those peroid irrational to the force. (6pi)
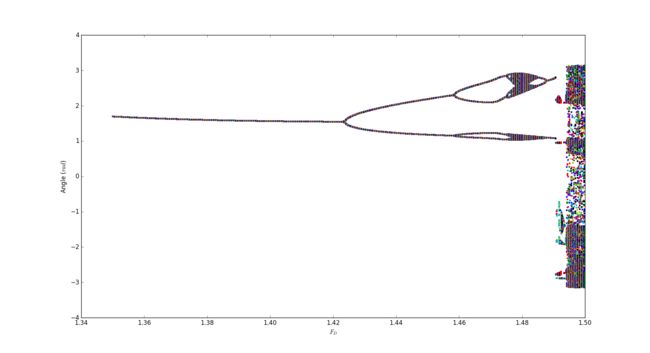
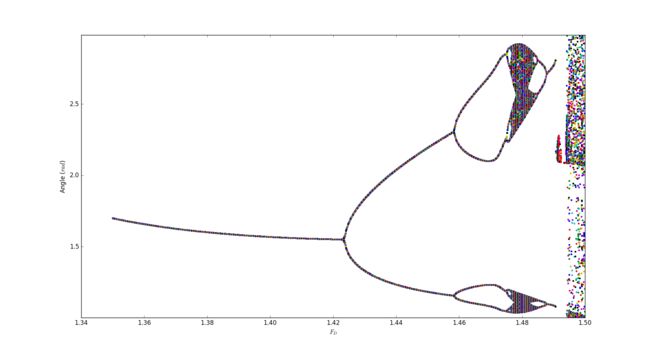
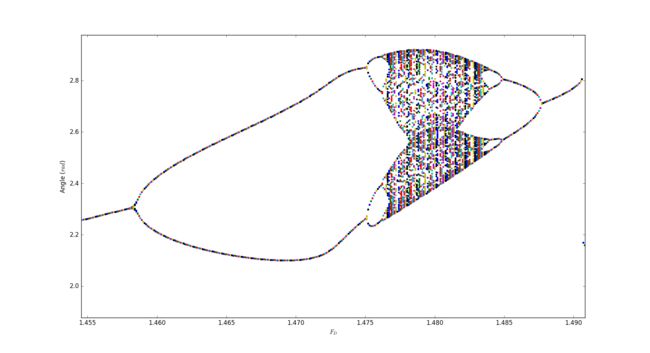
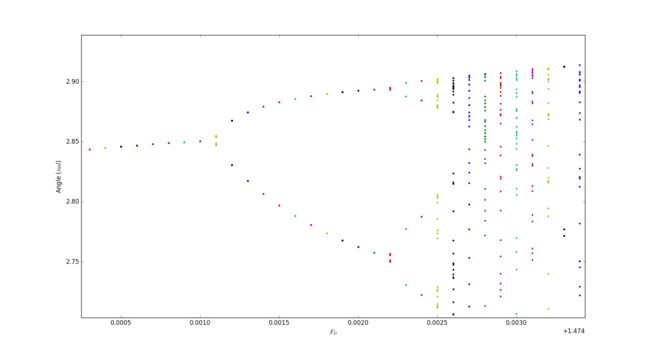
3.20
In this problem I try to draw the bifurcation diagram in which we can seen the change of peroid as the whole system going to state of chaos.
Original diagrem
Magnified diagrem 1
Magnified diagrem 2
Magnified diagrem 3
Conclution
I must apologize here that it took too long for my computer to work out the diagrem or I could use a higher precision and a clearer regularity of the process to the chaos could be shown directly in the graphs. Those pictures actually work like iterated function system which demostrate the causasion of chaos.
Acknowledge
- wikipedia
- My classmate Shuxu Hu(胡塾绪) who helped me on the drawing using vpython.
- Prof.Cai
How to contact me
- Wechat ID: bestsola
- Phone number: 18827628190
- E-mail: [email protected]