2019牛客多校赛 第一场 I题 Points Division (DP + 线段树)
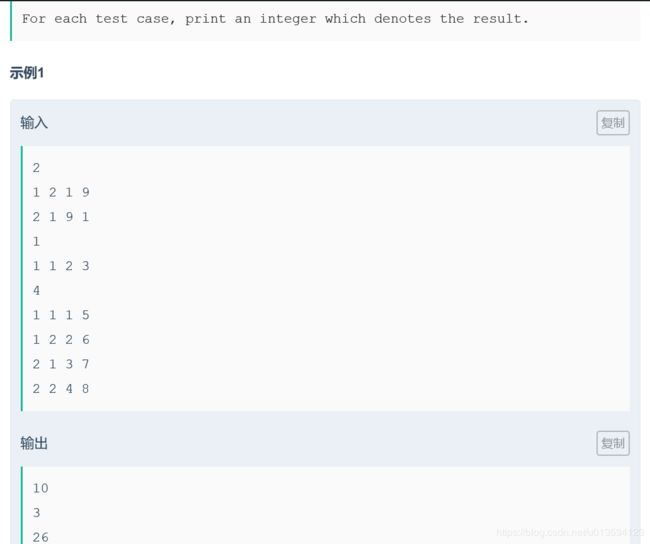
大致题意:给你n个点,第i个点在的位置为(xi,yi),有两个属性值(ai,bi)。现在让你把这n个点划分为A和B两个部分,使得最后不存在i∈A和j∈B,使得xi>=xj且yi<=yj。然后对于所有的划分方法,找到并输出
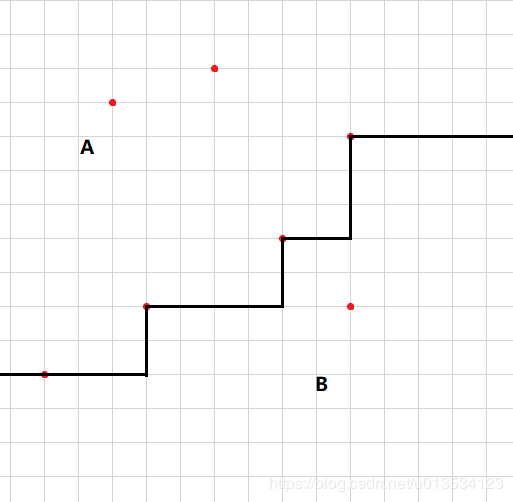
首先那个划分的限制条件看起来复杂,其实就是A中不存在点在B中任意一个点的右下角。根据这个限制,显然对于任意合法的划分,我都可以找到一条不下降的折线把所有点划分为两个部分。左上部分为A,右下部分为B。我们不妨移动这个折线,使得B中的部分点在边界上。如下图,是一种合法的方案。
现在要求的是两部分和的最大值,我们考虑DP。设dp[i]表示到目前为止,第i个点在折线上时的和的最大值。然后考虑每增加一个点会产生什么贡献。显然,增加一个点i之后,对于之前考虑过的比他高的点,他应该在B中,他的贡献是bi;相反,对于那些比他低的点,他应该在A中,他的贡献就是ai。于是,我们可以动态维护dp的数值,对于一个新加入的点i有:
另外,对于当前点i,此时当他在折线上时的最大值为:
具体到这道题,由于增加一个点产生的贡献其实是对区间的影响,然后转移的时候也需要求区间的最大值,所以我们可以把y坐标离散化并建立一棵线段树,维护区间最大值。需要注意的是,我们需要虚拟一个高度为0的点作为第一个点的参照。具体见代码:
#include
#define INF 0x3f3f3f3f3f3f3f3fll
#define LL long long
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
using namespace std;
const int N = 1e5 + 10;
struct node{int x,y,a,b;} p[N];
int n,m,num[N],tot;
struct ST
{
#define ls i<<1
#define rs i<<1|1
struct node
{
LL max,lazy;
int l,r;
} T[N<<2];
inline void push_up(int i)
{
T[i].max=max(T[ls].max,T[rs].max);
}
void build(int i,int l,int r)
{
T[i]=node{0,0,l,r};
if (l==r)
{
T[i].max=-INF;
T[i].lazy=0;
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
push_up(i);
}
inline void push_down(int i)
{
T[ls].lazy+=T[i].lazy;
T[rs].lazy+=T[i].lazy;
T[ls].max+=T[i].lazy;
T[rs].max+=T[i].lazy;
T[i].lazy=0;
}
void update(int i,int l,int r,LL x)
{
if (l>r) return;
if ((T[i].l==l)&&(T[i].r==r))
{
T[i].lazy+=x;
T[i].max+=x;
return;
}
if (T[i].lazy!=0) push_down(i);
int mid=(T[i].l+T[i].r)>>1;
if (mid>=r) update(ls,l,r,x);
else if (mid>1;
if (mid>=pos) upd(ls,pos,x);
else upd(rs,pos,x);
push_up(i);
}
LL getmax(int i,int l,int r)
{
if (l>r) return 0;
if ((T[i].l==l)&&(T[i].r==r)) return T[i].max;
if (T[i].lazy!=0) push_down(i);
int mid=(T[i].l+T[i].r)>>1;
if (mid>=r) return getmax(ls,l,r);
else if (midb.y:a.x

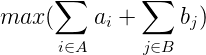
![\large dp[j]=\begin{cases}dp[j]+b_i &j<i,y_j>y_i\\dp[j]+a_i &j<i,y_j<y_i\end{cases}](http://img.e-com-net.com/image/info8/dbe5e09af6b94916a7b5220132d8577c.gif)