word2vec进阶之skim-gram和CBOW模型（Hierarchical Softmax、Negative Sampling）

系列目录（系列更新中）

• 第二讲 cs224n系列之word2vec & 词向量

• word2vec进阶之skim-gram和CBOW模型（Hierarchical Softmax、Negative Sampling）

• 第三讲 cs224n系列之skip-pram优化 & Global Vector by Manning & 词向量评价

语言模型

在统计自然语言处理中，语言模型指的是计算一个句子的概率模型。

传统的语言模型中词的表示是原始的、面向字符串的。两个语义相似的词的字符串可能完全不同，比如“番茄”和“西红柿”。这给所有NLP任务都带来了挑战——字符串本身无法储存语义信息。该挑战突出表现在模型的平滑问题上：标注语料是有限的，而语言整体是无限的，传统模型无法借力未标注的海量语料，只能靠人工设计平滑算法，而这些算法往往效果甚微。

神经概率语言模型（Neural Probabilistic Language Model）中词的表示是向量形式、面向语义的。两个语义相似的词对应的向量也是相似的，具体反映在夹角或距离上。甚至一些语义相似的二元词组中的词语对应的向量做线性减法之后得到的向量依然是相似的。词的向量表示可以显著提高传统NLP任务的性能，例如《基于神经网络的高性能依存句法分析器》中介绍的词、词性、依存关系的向量化对正确率的提升等。

从向量的角度来看，字符串形式的词语其实是更高维、更稀疏的向量。若词汇表大小为N，每个字符串形式的词语字典序为i，则其被表示为一个N维向量，该向量的第i维为1，其他维都为0。汉语的词汇量大约在十万这个量级，十万维的向量对计算来讲绝对是个维度灾难。而word2vec得到的词的向量形式（下文简称“词向量”，更学术化的翻译是“词嵌入”）则可以自由控制维度，一般是100左右。

---

word2vec

word2vec作为神经概率语言模型的输入，其本身其实是神经概率模型的副产品，是为了通过神经网络学习某个语言模型而产生的中间结果。具体来说，“某个语言模型”指的是“CBOW”和“Skip-gram”。具体学习过程会用到两个降低复杂度的近似方法——Hierarchical Softmax或Negative Sampling。两个模型乘以两种方法，一共有四种实现。这些内容就是本文理论部分要详细阐明的全部了

由于如下讲解有些跳跃，建议先读完基于Hierarchical Softmax的模型和
基于Negative Sampling的模型两篇帖子之后在看下面内容

综述Hierarchical Softmax

无论是哪种模型，其基本网络结构都是在下图的基础上，省略掉hidden layer：

为什么要去掉这一层呢？据说是因为word2vec的作者嫌从hidden layer到output layer的矩阵运算太多了。于是两种模型的网络结构是：

(这张图片有木有很熟悉？)

其中w(t)代表当前词语位于句子的位置t，同理定义其他记号。在窗口内（上图为窗口大小为5），除了当前词语之外的其他词语共同构成上下文。

基于Hierarchical Softmax的CBOW模型

原理
CBOW 是 Continuous Bag-of-Words Model 的缩写，是一种根据上下文的词语预测当前词语的出现概率的模型。其图示如上图左。

CBOW是已知上下文，估算当前词语的语言模型。其学习目标是最大化对数似然函数：
$$\varsigma =\sum _{wϵC}logp(w|Context(w))$$

其中，w表示语料库C中任意一个词。从上图可以看出，对于CBOW，

• 输入层是上下文的词语的词向量（什么！我们不是在训练词向量吗？不不不，我们是在训练CBOW模型，词向量只是个副产品，确切来说，是CBOW模型的一个参数。训练开始的时候，词向量是个随机值，随着训练的进行不断被更新）。
• 投影层对其求和，所谓求和，就是简单的向量加法。
• 输出层输出最可能的w。由于语料库中词汇量是固定的|C|个，所以上述过程其实可以看做一个多分类问题。给定特征，从|C|个分类中挑一个。

对于神经网络模型多分类，最朴素的做法是softmax回归：

softmax回归需要对语料库中每个词语（类）都计算一遍输出概率并进行归一化，在几十万词汇量的语料上无疑是令人头疼的。

不用softmax怎么样？比如SVM中的多分类，我们都知道其多分类是由二分类组合而来的：

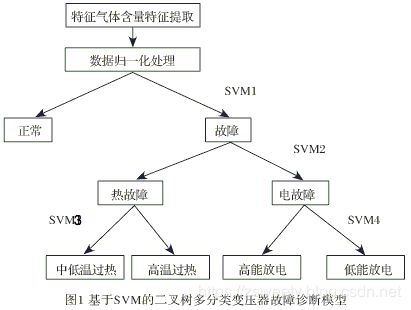
这是一种二叉树结构，应用到word2vec中被作者称为Hierarchical Softmax：

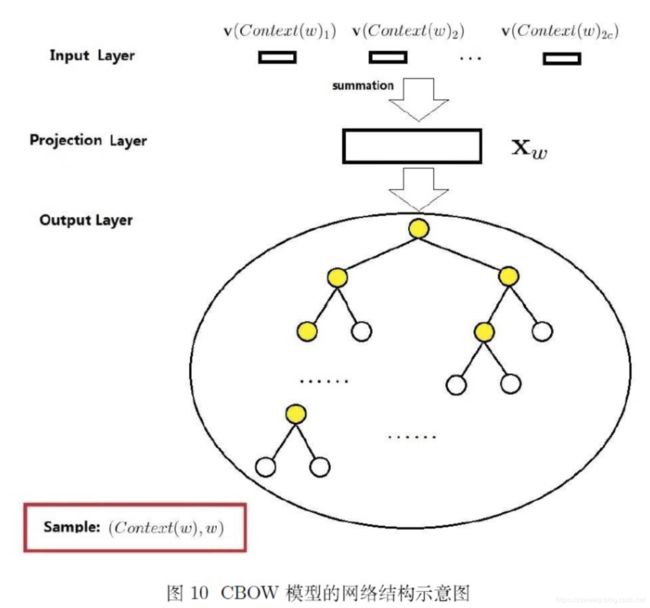
上图输出层的树形结构即为Hierarchical Softmax。

非叶子节点相当于一个神经元（感知机，我认为逻辑斯谛回归就是感知机的输出代入$f(x)=1/(1+e^x)$，二分类决策输出1或0，分别代表向下左转或向下右转；每个叶子节点代表语料库中的一个词语，于是每个词语都可以被01唯一地编码，并且其编码序列对应一个事件序列，于是我们可以计算条件概率 $p(w|Context(w))$

在开始计算之前，还是得引入一些符号：

• $p^w$从根结点出发到达w对应叶子结点的路径.

• $l^w$路径中包含结点的个数

• $p_1^w,p_1^w,...p_{l^w}^w$路径$p^w$中的各个节点

• $d_1^w,d_1^w,...d_{l^w}^wϵ0,1$ 词w的编码，$d_1^w$表示路径屏幕快照$p^w$第j个节点对应的编码（根节点无编码）

• ${\theta }_1^w,{\theta }_1^w,...{\theta }_{l^w}^wϵ\mathbb{R}$路径 $p^w$ 中非叶节点对应的参数向量

于是可以给出w的条件概率：

$$p(w|Context(w))=\prod _{j=2}^{l^w}p(d_n^w|x_w,{\theta }_{j-1}^w)$$

这是个简单明了的式子，从根节点到叶节点经过了$l^w-1$个节点，编码从下标2开始（根节点无编码），对应的参数向量下标从1开始（根节点为1）。

考虑到d只有0和1两种取值，我们可以用指数形式方便地将其写到一起：

我们的目标函数取对数似然：

$$\varsigma =\sum _{wϵC}logp(w|Context(w))$$

将$p(w|Context(w))$代入上式，有

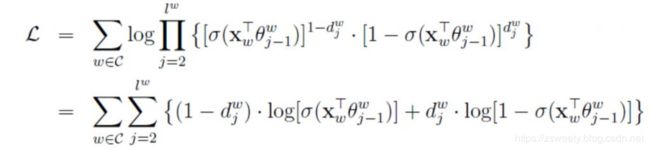
这也很直白，连乘的对数换成求和。不过还是有点长，我们把每一项简记为：

怎么最大化对数似然函数呢？分别最大化每一项即可（这应该是一种近似，最大化某一项不一定使整体增大，具体收敛的证明还不清楚）。怎么最大化每一项呢？先求函数对每个变量的偏导数，对每一个样本，代入偏导数表达式得到函数在该维度的增长梯度，然后让对应参数加上这个梯度，函数在这个维度上就增长了。这种白话描述的算法在学术上叫随机梯度上升法，详见更规范的描述。
每一项有两个参数，一个是每个节点的参数向量${\theta }_{j-1}^w$，另一个是输出层的输入$ X_w $，我们分别对其求偏导数：

因为sigmoid函数的导数有个很棒的形式：

于是代入上上式得到：

合并同类项得到：
于是${\theta }_{j-1}^w$的更新表达式就得到了：

基于Hierarchical Softmax的skip-gram模型

参见：连接

基于Hierarchical Softmax的CBOW与skip-gram的异同

异：

• CBOW是通过上下文预测目标词语，但是skip-gram是预测上下文（我感觉同样可以预测同义词。。。），所以在Hierarchical softmax中，skip-gram中的映射层是直接copy的输入层的，但是在CBOW中是将输入的上下文词向量到达映射层是做了sum运算。 因此导致的最终的$\theta$和词向量的更新也稍有区别
  CBOW：
  
  （关于这里的w上面加个帽子就是上下文的所有词向量，他们的更新方式相同，可通过前面的介绍详细了解）
  skip-gram：
  
  
• 使用的Hierarchical softmax模型是一样的，除了上面的不同点我目前理解还找不出区别

Negative Sampling

相关链接：

• word2vec原理(三) 基于Negative Sampling的模型
• Negative Sampling

参考链接：

• word2vec原理推导与代码分析
• word2vec原理(二) 基于Hierarchical Softmax的模型
• word2vec原理(三) 基于Negative Sampling的模型
• Negative Sampling