算法细节系列（18）：凸包的三种计算

算法细节系列（18）：凸包的三种计算

详细代码可以fork下Github上leetcode项目，不定期更新。

题目摘自leetcode：
1. Leetcode 587. Erect the Fence

刷一道周赛题时遇到了相关的凸包计算，特此整理下，方便日后复查。不得不吐槽下，网上有很多关于凸包的算法，但完整实现的却不多，所以本文借着leetcode提供的测试数据，把一些基本的凸包算法都实现下，顺便在此基础上说说原理。

Leetcode 587. Erect the Fence

Problem:

There are some trees, where each tree is represented by (x,y) coordinate in a two-dimensional garden. Your job is to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Your task is to help find the coordinates of trees which are exactly located on the fence perimeter.

Example 1:

Input: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
Output: [[1,1],[2,0],[4,2],[3,3],[2,4]]
Explanation:

Example 2:

Input: [[1,2],[2,2],[4,2]]
Output: [[1,2],[2,2],[4,2]]
Explanation:

Even you only have trees in a line, you need to use rope to enclose them.

Note:

• All trees should be enclosed together. You cannot cut the rope to enclose trees that will separate them in more than one group.
• All input integers will range from 0 to 100.
• The garden has at least one tree.
• All coordinates are distinct.
• Input points have NO order. No order required for output.

解法一（穷尽搜索）

参考博文【凸包问题的五种解法】
当然非暴力解法莫属，想法很简单，我们知道凸包的性质，凸包一定是【最外围】的那些点圈成，所以假设有n个点，那么最多可以构造出 n(n−1)2 条边，算法如下：
1. 选定一条边，遍历其他n-2个点，如果所有点都在该条边的一侧，则加入凸包集合。
2. 不断重复步骤1，直到所有边都被遍历过。

如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢？（坐标：p1(x1,y1)，p2(x2,y2)，p3(x3,y3)）我们可以计算：

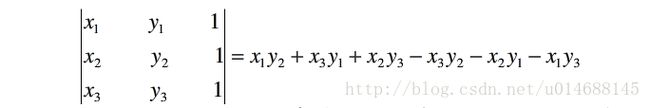
当上式结果为正时，p3在直线 p1p2 的左侧；当结果为负时，p3在直线 p1p2 的右边。

代码如下：

    public List outerTrees(Point[] points) {
        Set ans = new HashSet<>();
        if (points.length == 1){
            ans.add(points[0]);
            return new ArrayList<>(ans);
        }
        for (int i = 0; i < points.length; i++){
            for (int j = i + 1; j < points.length; j++){
                int oneSide = 0;
                for (int k = 0; k < points.length; k++){
                    if (k == i || k == j) continue;
                    if (calcuTriangle(points[i], points[j], points[k]) > 0){
                        oneSide++;
                    }
                }

                if (oneSide == points.length-2 || oneSide == 0){
                    ans.add(points[i]);
                    ans.add(points[j]);
                }

                int otherSide = 0;
                for (int k = 0; k < points.length; k++){
                    if (k == i || k == j) continue;
                    if (calcuTriangle(points[i], points[j], points[k]) < 0){
                        otherSide++;
                    }
                }

                if (otherSide == points.length-2 || otherSide == 0){
                    ans.add(points[i]);
                    ans.add(points[j]);
                }

            }
        }

        return new ArrayList<>(ans);
    }
    private int calcuTriangle(Point a1, Point a2, Point a3) {
        return a1.x * a2.y + a3.x * a1.y + a2.x * a3.y 
                - a3.x * a2.y - a2.x * a1.y - a1.x * a3.y;
    }

在真实数据情况下，可能所有点都在直线的上侧，也有可能所有点在直线的下侧，所以在内循环中，会有两个方向的计算。代码思路很简单，没太多有意思的东西。

上述做法是一种最蠢的无记忆手段，而凸包有很多性质可以利用。就把这些点放在平面上来看，如下图：

就拿暴力做法而言，在求 p0p1 时，遍历了所有的点。此时，它会继续遍历 p0p2 ，而由图知道这不可能是凸包的边界，可算法还得继续求。

解法二（分而治之）

凸包有几个比较好的性质，如按横坐标排序，横坐标最小和横坐标最大的点一定是凸包上的边界点。如何证明？（反证法cut&&paste）

如上图中， p12和P3 ，对纵坐标也是一个道理。嘿，此时我们就能想到另外一个有意思的方法，分治。

算法步骤如下：
1. 把所有的点都放在二维坐标系里面。那么横坐标最小和最大的两个点 P1 和 Pn 一定是凸包上的点。直线 P1Pn 把点集分成了两部分，即 X 轴上面和下面两部分，分别叫做上包和下包。
2. 对上包：求距离直线 P1Pn 最远的点，即下图中的点 Pmax 。
3. 作直线 P1Pmax 、PnPmax，把直线 P1Pmax 左侧的点当成是上包，把直线 PnPmax 右侧的点也当成是上包。
4. 重复步骤 2、3。
5. 对下包也作类似操作。

典型的划分，用相同的方法求解子问题。我一直在想为什么分治法就把所谓的时间复杂度就降低到了 O(nlogn) ，吼吼，简单来说，就是可以利用一些性质把部分没必要的遍历给去除了，如上图，当确定了 P1Pmax 这条直线后，求上包的过程中，完全可以去除其右下侧的所有点，所以该整体问题的规模一下子缩小了两倍还多。而我们知道，已知样本总量为 n ，每次能缩小到原来的 n2 ，该递归的深度就仅为 O(logn) ，而每层需要遍历n次，所以有 O(nlogn) .

使用分治需要注意，这种 n到n2 的大问题变子问题并不时刻正确，我们得确保子问题的求解方法和大问题的求解方法一致，且最终能够终结到基础情形。

光说不练假把式，代码如下：

    public List outerTrees(Point[] points) {
        List pp = Arrays.asList(points);
        helper(pp,true);
        helper(pp, false);
        return new ArrayList<>(ans);
    }

    Set ans = new HashSet<>();
    private void helper(List points, boolean calcuConvex){
        if (points.size() == 0) return;
        Collections.sort(points, new Comparator() {
            @Override
            public int compare(Point o1, Point o2) {
                return o1.x != o2.x ? o1.x - o2.x : o1.y - o2.y;
            }
        });
        int fir = 0;
        int lst = points.size() - 1;

        ans.add(points.get(fir));
        ans.add(points.get(lst));

        if (points.size() == 2)
            return;

        // oneLine
        boolean isLine = true;
        for (int i = 0; i < points.size(); i++) {
            if (i == fir || i == lst)
                continue;
            if (calcuTriangle(points.get(fir), points.get(lst), points.get(i)) != 0) {
                isLine = false;
                break;
            }
        }
        if (isLine) {
            ans.addAll(points);
            return;
        }

        int maxIndex = -1;
        int max = 0;
        for (int i = 0; i < points.size(); i++) {
            if (i == fir || i == lst)
                continue;
            // 上凸包
            if (calcuConvex && calcuTriangle(points.get(fir), points.get(lst), points.get(i)) > max) {
                maxIndex = i;
                max = calcuTriangle(points.get(fir), points.get(lst), points.get(i));
            }
            // 下凸包
            if (!calcuConvex && -calcuTriangle(points.get(fir), points.get(lst), points.get(i)) > max) {
                maxIndex = i;
                max = -calcuTriangle(points.get(fir), points.get(lst), points.get(i));
            }
        }

        if (maxIndex == -1) {
            return;
        }

        List c1 = new ArrayList<>();
        split(fir, maxIndex, points, c1, calcuConvex);
        helper(c1,calcuConvex);

        List c2 = new ArrayList<>();
        split(lst, maxIndex, points, c2, !calcuConvex);
        helper(c2,calcuConvex);
    }

    private void split(int a1, int a2, List points, List part1, boolean isConvex) {
        for (int i = 0; i < points.size(); i++) {
            if (i == a1 || i == a2) {
                part1.add(points.get(i));
                continue;
            }
            if (isConvex && calcuTriangle(points.get(a1), points.get(a2), points.get(i)) >= 0) {
                part1.add(points.get(i));
            }

            if (!isConvex && calcuTriangle(points.get(a1), points.get(a2), points.get(i)) <= 0) {
                part1.add(points.get(i));
            }
        }
    }

    private int calcuTriangle(Point a1, Point a2, Point a3) {
        return a1.x * a2.y + a3.x * a1.y + a2.x * a3.y 
                - a3.x * a2.y - a2.x * a1.y - a1.x * a3.y;
    }

分治手段非常强大，通过确定三个边界点，把该问题划分成四个子问题，一下子把复杂度给降下来了，而真正降低复杂度的原因就在于我们可以排除一些没必要点对遍历。而所使用的性质为：

已知凸包边界的三个点，我们就可以对点集进行划分。而三个点一定在横坐标最小的一个和横坐标最大的一个，还有一个可以选择与该两点构成三角形面积最大的一点。

解法三（Graham扫描法）

我给了它一个新名字，边界扫描法。用到的性质和解法二密切相关，首先也需要对某个维度进行从小达到排序。这样我们就能确定其中一个顶点了，我们选择横坐标最小的那个点作为整个坐标的原点。

算法更新过程如上图所示。

算法步骤：
1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的P0。
2. 把所有点的坐标平移一下，使 P0 作为原点，如上图。
3. 计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。例如上图得到的结果为 P1，P2，P3，P4，P5，P6，P7，P8。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
（以上是准备步骤，以下开始求凸包）
以上，我们已经知道了凸包上的第一个点 P0 和第二个点 P1，我们把它们放在栈里面。现在从步骤3求得的那个结果里，把 P1 后面的那个点拿出来做当前点，即 P2 。接下来开始找第三个点：
4. 连接P0和栈顶的那个点，得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
6. 当前点是凸包上的点，把它压入栈，执行步骤7。
7. 检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。

算法思路很清楚，但一开始，我始终不明白为什么要进行排序，如果我们知道一个顶点，直接从那个顶点出发不断更新最外圈不就好了么。先来看看具体代码：

public List outerTrees(Point[] points) {
        return GrahamScan(points);
    }

    private List GrahamScan(Point[] points){
        int n = points.length;
        if (n <= 2) return Arrays.asList(points);
        //排序的原因是什么
        Arrays.sort(points,new Comparator(){
            @Override
            public int compare(Point o1, Point o2) {
                return o1.y != o2.y ? o1.y - o2.y : o1.x - o2.x;
            }
        });

        int[] stack = new int[n+2];
        int p = 0;
        //一个O(n)的循环
        for (int i = 0; i < n; i++) {
            while (p >= 2 && cross(points[stack[p - 2]], points[i], points[stack[p - 1]]) > 0)
                p--;
            stack[p++] = i;
        }

        int inf = p + 1;
        for (int i = n -2; i >= 0; i--){
            if (equal(points[stack[p-2]], points[i])) continue;
            while (p >= inf && cross(points[stack[p-2]], points[i], points[stack[p-1]]) > 0)
                p--;
            stack[p++] = i;
        }

        int len = Math.max(p - 1, 1);
        List ret = new ArrayList<>();
        for (int i = 0; i < len; i++){
            ret.add(points[stack[i]]);
        }

        return ret;
    }

    private int cross(Point o, Point a, Point b){
        return (a.x-o.x)*(b.y-o.y) - (a.y - o.y) * (b.x - o.x);
    }

    private boolean equal(Point a, Point b){
        return a.x == b.x && a.y == b.y;
    }

其实上述代码，可以有一个复杂版本，即 O(n2) 的算法，也就是在那个单重循环中，第一步是更新边界点，一旦边界点被更新，那么从该边界点（栈中的第一个元素）重新遍历剩余的点，找到一条新的边界即可。

而排序给我们带来了一个极大的好处，我们可以直接按照顺序遍历所有顶点一次。

因为我们知道，在一个y值更低的点中，如果存在一个y值比它高的点，那么该边界一定是与那个y值更高的点相连。所以在保证纵轴有序的情况下，我们就能严格控遍历顺序（带来的好处仅需遍历一次），从而保证答案正确。

或者你还可以这么想，就拿上述代码来分析，如果坐标点并没有严格有序，那么更新算法随机选择点进行边界更新，若选中了一个y值较高的点，但它可能因为极角不够大而被替代，而一旦替代，该点就无法再用（只遍历一次），但实际情况它是一个有效的边界点。这就导致了边界寻找顺序错乱。

所以总结下凸包算法的核心：

利用了凸包边界在更新过程中，总是不断向上或者平行寻找边界点的性质，有了它，才能够使得我们在更新之前对坐标点进行排序，从而让更新规则按照我们想要的路径执行，减少时间复杂度。