数据结构之二叉树的创建
文章开头首先要感谢一下国嵌嵌入式教育的工作者们。
创建二叉树
二叉树不仅比通用树结构简练,而且同时拥有通用树相同的操作。要想创建二叉树,首先就得了解一下二叉树的存储结构。已知二叉树的存储结构分为顺序存储结构和链式存储结构。其中链式存储结构又分为二叉链表和三叉链表。
1. 顺序存储结构:
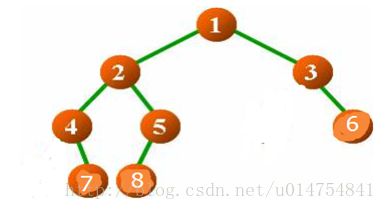
按照顺序存储结构的定义,在此约定用一组地址连续的存储单元一次自上而下、自左至右存储完全二叉树上的节点元素,即将完全二叉树上编号为i的结点元素存储在如上定义的一维数组中下标为i-1的分量中。如下表1所示为图1所示的完全二叉树的顺序存储结构:
表1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
对于一般二叉树,则将其每一个结点与完全二叉树的结点相对照,存储在一维数组的相应分量中,如下表2所示图2所示的非完全二叉树的顺序存储结构::
表2
1 |
2 |
3 |
4 |
5 |
0 |
6 |
0 |
7 |
8 |
图中“0”表示不存在此结点。由此可见顺序存储结构仅适用于完全二叉树。因为,在最坏的情况下,一个深度为k且只有k个结点的单枝树(树中不存在度为2的结点)却需要长度为2k-1的一维数组。造成存储内存的浪费。
链式存储结构:
设计不同的结点结构可构成不同形式的链式存储结构。由二叉树的定义得知,二叉树的结点由一个数据元素和分别指向其左、右子树的两个分支构成,则表示二叉树的链表中的结点至少包含3个域:数据域和左、右指针域。如下所示:
Lchid |
Data |
Rchild |
有时,为了便于找到结点的双亲,则还可在结点结构中增加一个指向其双亲结点的指针域,如下所示:
Lchild |
Data |
Parent |
Rchild |
利用这两种结点结构所得的二叉树的存储结构分别称之为二叉链表和三叉链表。链表的头指针指向二叉树的根结点。因此,我们可知在含有n个节点的二叉链表中有n+1个空链域用于存放二叉树结点。到此,我们应该明白可以通过单链表的实现思想来创建二叉树。单链表内容参考单链表C语言实现
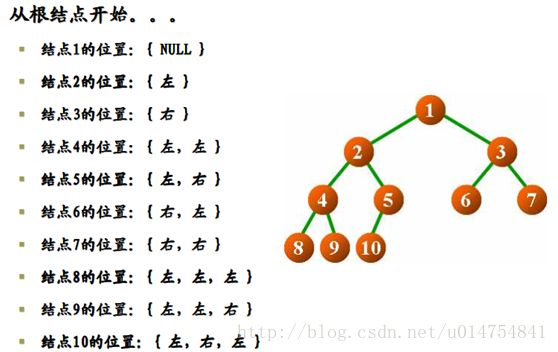
我们接下来讲一下如何通过二叉链表链式存储结构对二叉树进行操作,其重点就是如何在二叉树中定位结点的位置?那么如何定位呢?
现实生活中我们总会遇到问路的情况,指路的人一般都会说直走、到哪个路口左拐,到哪个路口右拐。这就让我们联想到二叉树的结点是否可以类比成现实中的路口,它的两个子树是否可以当做左拐或右拐呢?
因此,前辈们想出了指路法定位结点:
指路法通过根结点与目标结点的相对位置进行定位,指路法可以避开二叉树递归的性质“线性”定位。
思想:在C语言中可以利用bit位进行指路。。。
用结构体来定义二叉树中的指针域,二叉树的头结点与数据域也可以用结构体实现。
二叉树的重点操作是定位,下面我们看一下定位操作:
定位的关键技巧:
1.利用二进制中的0和1分别表示left和right;
2.位运算是实现指路法的基础。
至此,我们就可以来实现二叉树的相关操作了,上代码。
首先定义相关结构体及其他变量
#define BT_LEFT 0 // 左边
#define BT_RIGHT 1 // 右边
// 定义新数据类型,用于封装函数
typedef void BTree;
typedef unsigned long long BTPos;
// 定义二叉树左右指针结构体
typedef struct _tag_BTreeNode BTreeNode;
struct _tag_BTreeNode
{
BTreeNode* left; // 二叉树左结点指针
BTreeNode* right; // 二叉树右结点指针
};
// 定义二叉树根结点结构体
typedef struct _tag_BTree TBTree;
struct _tag_BTree
{
int count; // 记录二叉树结点个数
BTreeNode* root; // 二叉树结点指针结构体,指向根结点
};// 创建二叉树
BTree* BTree_Create() // O(1)
{
// 定义二叉树结点结构体变量,并申请内存
TBTree* ret = (TBTree*)malloc(sizeof(TBTree));
// 申请成功,初始化二叉树为空树
if( ret != NULL )
{
ret->count = 0;
ret->root = NULL;
}
return ret;
}创建二叉树比较简单,等同于简单的单链表创建方法。所以销毁和清空二叉树也会单链表的操作雷同。
2.销毁与清空单链表
// 销毁二叉树
void BTree_Destroy(BTree* tree) // O(1)
{
free(tree); // 释放内存
}
// 清空二叉树
void BTree_Clear(BTree* tree) // O(1)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 参数合法性OK,将二叉树置为空树
if( btree != NULL )
{
btree->count = 0;
btree->root = NULL;
}
}3.插入结点
插入结点是二叉树操作的重点,代码如下:
// 在二叉树指定位置pos插入结点node
// pos:定位的方向,二进制:0表示左,1表示右
// count:定位次数,移动指针次数
// flag:插入方向 BT_LEFT or BT_RIGHT
int BTree_Insert(BTree* tree, BTreeNode* node, BTPos pos, int count, int flag) // O(n)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 入口参数合法性检查,插入的二叉树不为空,插入的结点不为空,插入方向正确
int ret = (btree != NULL) && (node != NULL) && ((flag == BT_LEFT) || (flag == BT_RIGHT));
int bit = 0;
// 入口参数合法性ok
if( ret )
{
// 定义二叉树左右指针结构体临时变量
BTreeNode* parent = NULL;
// 定义二叉树左右指针结构体变量,存放当前结点地址
BTreeNode* current = btree->root;
// 初始化插入结点的左右指针地址,默认为NULL
node->left = NULL;
node->right = NULL;
// 开始定位 定位次数不为零,插入的位置不是根结点
while( (count > 0) && (current != NULL) )
{
// 取定位方向参数最右边bit位用于判断左右
bit = pos & 1;
pos = pos >> 1;
// 临时变量更新当前指针,保存插入结点位置的双亲指针
parent = current;
// 左边,向左移动指针
if( bit == BT_LEFT )
{
current = current->left; // 将当前结点指针指向左边子结点指针
}
// 右边,向右移动指针
else if( bit == BT_RIGHT )
{
current = current->right; // 将当前结点指针指向右边子结点指针
}
// 定位次数减1
count--;
}
// 定位完成后,判断待插入结点的插入位置
// 左边
if( flag == BT_LEFT )
{
node->left = current; // 将带插入结点的左指针指向当前结点
}
// 右边
else if( flag == BT_RIGHT )
{
node->right = current; // 将待插入结点的右指针指向当前结点
}
// 当前结点指针不为空,即不是根结点
if( parent != NULL )
{
// 左边
if( bit == BT_LEFT )
{
parent->left = node; // 将插入结点位置的双亲指针的左指针指向待插入结点
}
// 右边
else if( bit == BT_RIGHT )
{
parent->right = node; // 将插入结点位置的双亲指针的右指针指向待插入结点
}
}
// 插入的是首结点,即根结点
else
{
btree->root = node; // 将根结点指向待插入结点
}
// 二叉树结点个数加1
btree->count++;
}
return ret;
}通过上面的代码,我们发现二叉树的插入与单链表的参入操作实现方式基本雷同,不同的就是二叉树指针分左右,双指针操作,而单链表操作的指针只有一个next。插入的重点是先根据参数定好位置同时时刻更新找到的新位置,然后根据插入的方向将找到的位置的左或右左右指针指向要插入的结点地址,将要插入的结点地址的左右指针指向相对应的原来位置的左右指针位置。
4.显示二叉树
插入的二叉树,就要验证一下插入的是否正确,所以我们通过二叉树的显示函数来显示二叉树的元素,来验证插入的正确性。代码如下:
// 显示二叉树
void BTree_Display(BTree* tree, BTree_Printf* pFunc, int gap, char div) // O(n)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 合法性检查OK,调用显示递归函数
if( btree != NULL )
{
recursive_display(btree->root, pFunc, 0, gap, div);
}
}同通用树一样,二叉树的显示函数也需要递归来实现,递归实现代码如下:
// 显示递归函数
static void recursive_display(BTreeNode* node, BTree_Printf* pFunc, int format, int gap, char div) // O(n)
{
int i = 0;
// 合法性检查OK
if( (node != NULL) && (pFunc != NULL) )
{
// 打印格式符
for(i=0; ileft != NULL) || (node->right != NULL) )
{
recursive_display(node->left, pFunc, format + gap, gap, div); // 调用递归函数打印左子树结点
recursive_display(node->right, pFunc, format + gap, gap, div); // 调用递归函数打印右子树结点
}
}
// 根结点为空
else
{
// 打印格式符
for(i=0; i 与通用树不同的地方就是二叉树需要分左右显示。
5.删除指定结点
// 删除指定位置的结点
BTreeNode* BTree_Delete(BTree* tree, BTPos pos, int count) // O(n)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 定义返回变量
BTreeNode* ret = NULL;
int bit = 0;
// 入口参数合法性检查ok
if( btree != NULL )
{
// 定义二叉树左右指针结构体临时变量
BTreeNode* parent = NULL;
// 定义二叉树左右指针结构体变量,存放当前结点地址
BTreeNode* current = btree->root;
// 开始定位 定位次数不为零,删除的位置不是根结点
while( (count > 0) && (current != NULL) )
{
// 取定位方向参数最右边bit位用于判断左右
bit = pos & 1;
pos = pos >> 1;
// 临时变量更新当前指针,保存删除结点位置的双亲指针
parent = current;
// 左边,向左移动指针
if( bit == BT_LEFT )
{
current = current->left; // 将删除结点位置的双亲指针的左指针指向待删除结点
}
// 右边,向右移动指针
else if( bit == BT_RIGHT )
{
current = current->right; // 将删除结点位置的双亲指针的右指针指向待删除结点
}
// 定位次数减1
count--;
}
// 当前结点指针不为空,即不是根结点
if( parent != NULL )
{
// 左边
if( bit == BT_LEFT )
{
parent->left = NULL; // 将结点左子树位置指向空指针,即删除左结点
}
// 右边
else if( bit == BT_RIGHT )
{
parent->right = NULL; // 将结点右子树位置指向空指针,即删除右结点
}
}
// 删除的是首结点,即根结点
else
{
btree->root = NULL; // 将根结点指向空指针,即删除所有结点
}
// 返回删除元素结点
ret = current;
// 更新二叉树结点个数,结点个数减去删除的结点个数
btree->count = btree->count - recursive_count(ret);
}
return ret;
}删除结点的操作重点和插入一样,首先通过参数定位到要删除的结点,然后根据要删除的方向将该结点的左或右指针指向NULL即可。需要主要的是二叉树的数量更新不是单单的减1就行的,这得需要根据删除的结点来计算出该结点相应子树下的所有结点个数,然后减去这个个数才行btree->count = btree->count - recursive_count(ret);
,所以我们同个一个递归函数求结点个数。递归函数代码如下:
// 求二叉树结点子树结点个数
static int recursive_count(BTreeNode* root) // O(n)
{
int ret = 0;
// 合法性检查ok
if( root != NULL )
{
ret = recursive_count(root->left) + 1 + recursive_count(root->right); // 调用递归函数计算个数
}
// 返回个数
return ret;
}6.获取指定结点
// 获取指定位置的结点
BTreeNode* BTree_Get(BTree* tree, BTPos pos, int count) // O(n)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 定义返回变量
BTreeNode* ret = NULL;
int bit = 0;
// 入口参数合法性检查ok
if( btree != NULL )
{
// 定义二叉树左右指针结构体变量,存放当前结点地址
BTreeNode* current = btree->root;
// 开始定位 定位次数不为零,删除的位置不是根结点
while( (count > 0) && (current != NULL) )
{
// 取定位方向参数最右边bit位用于判断左右
bit = pos & 1;
pos = pos >> 1;
// 左边,向左移动指针
if( bit == BT_LEFT )
{
current = current->left;
}
// 右边,向右移动指针
else if( bit == BT_RIGHT )
{
current = current->right;
}
// 定位次数减1
count--;
}
ret = current;
}
return ret;
}获取指定位置的结点,首先就是定位置到要获取的位置,然后返回该结点的地址即可。
7.获取根结点
// 获取根结点
BTreeNode* BTree_Root(BTree* tree) // O(1)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 定义返回变量
BTreeNode* ret = NULL;
// 入口参数合法性检查ok,返回根结点地址
if( btree != NULL )
{
ret = btree->root;
}
return ret;
}获取根结点就是获取二叉树的头结点,直接返回头结点地址即可。
8.获取二叉树的高度(深度)
// 获取二叉树高度
int BTree_Height(BTree* tree) // O(n)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 定义返回变量
int ret = 0;
// 入口参数合法性检查ok,调用递归函数求二叉树高度
if( btree != NULL )
{
ret = recursive_height(btree->root);
}
// 返回二叉树高度
return ret;
}和通用树一样,二叉树的高度获取也需要递归来实现,递归函数代码如下:
// 求二叉树高度递归函数
static int recursive_height(BTreeNode* root) // O(n)
{
// 定义返回值变量
int ret = 0;
// 入口参数合法性检查OK
if( root != NULL )
{
int lh = recursive_height(root->left); // 求左子树高度
int rh = recursive_height(root->right); // 求右子树高度
// 求左右子树高度最大值
ret = ((lh > rh) ? lh : rh) + 1;
}
// 返回二叉树高度
return ret;
}分别求左右子树的高度,然后比较出最大值返回。
9.获取二叉树的度
// 获取二叉树度
int BTree_Degree(BTree* tree) // O(n)
{
// 定义二叉树结点结构体变量,强制转换入口参数
TBTree* btree = (TBTree*)tree;
// 定义返回变量
int ret = 0;
// 入口参数合法性检查ok,调用求二叉树度递归函数
if( btree != NULL )
{
ret = recursive_degree(btree->root);
}
// 返回二叉树的度
return ret;
}// 求二叉树度递归函数,最大度为2
static int recursive_degree(BTreeNode* root) // O(n)
{
// 定义返回值变量
int ret = 0;
// 入口参数合法性检查OK
if( root != NULL )
{
// 左子树结点不为空,度加1
if( root->left != NULL )
{
ret++;
}
// 右子树结点不为空,度加1
if( root->right != NULL )
{
ret++;
}
// 度为1,调用递归函数求其他结点度
if( ret == 1 )
{
int ld = recursive_degree(root->left); // 求左子树结点的度
int rd = recursive_degree(root->right); // 求右子树结点的度
// 求左子树结点度的最大值
if( ret < ld )
{
ret = ld;
}
// 求右子树结点度的最大值
if( ret < rd )
{
ret = rd;
}
}
}
// 返回度
return ret;
}因为二叉树的度最大也就是2,所以只有在当前求得度为1时才需要调用递归函数来求其他子树结点的度。
验证代码如下:
#include
#include
#include "BTree.h"
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
// 定义二叉树数据域结构体
struct Node
{
BTreeNode header;
char v;
};
// 定义打印内容函数
void printf_data(BTreeNode* node)
{
if( node != NULL )
{
printf("%c", ((struct Node*)node)->v);
}
}
int main(int argc, char *argv[])
{
// 创建二叉树
BTree* tree = BTree_Create();
// 定义要插入结点元素
struct Node n1 = {{NULL, NULL}, 'A'};
struct Node n2 = {{NULL, NULL}, 'B'};
struct Node n3 = {{NULL, NULL}, 'C'};
struct Node n4 = {{NULL, NULL}, 'D'};
struct Node n5 = {{NULL, NULL}, 'E'};
struct Node n6 = {{NULL, NULL}, 'F'};
// 插入结点元素
BTree_Insert(tree, (BTreeNode*)&n1, 0, 0, 0);
BTree_Insert(tree, (BTreeNode*)&n2, 0x00, 1, 0);
BTree_Insert(tree, (BTreeNode*)&n3, 0x01, 1, 0);
BTree_Insert(tree, (BTreeNode*)&n4, 0x00, 2, 0);
BTree_Insert(tree, (BTreeNode*)&n5, 0x02, 2, 0);
BTree_Insert(tree, (BTreeNode*)&n6, 0x02, 3, 0);
// 打印相应提示内容
printf("Height: %d\n", BTree_Height(tree));
printf("Degree: %d\n", BTree_Degree(tree));
printf("Count: %d\n", BTree_Count(tree));
printf("Position At (0x02, 2): %c\n", ((struct Node*)BTree_Get(tree, 0x02, 2))->v);
printf("Full Tree: \n");
// 显示二叉树
BTree_Display(tree, printf_data, 4, '-');
// 测试删除结点功能
BTree_Delete(tree, 0x00, 1);
// 打印相应提示内容
printf("After Delete B: \n");
printf("Height: %d\n", BTree_Height(tree));
printf("Degree: %d\n", BTree_Degree(tree));
printf("Count: %d\n", BTree_Count(tree));
printf("Full Tree: \n");
// 显示删除结点后的二叉树
BTree_Display(tree, printf_data, 4, '-');
// 测试清空二叉树功能
BTree_Clear(tree);
// 打印相应提示内容
printf("After Clear: \n");
printf("Height: %d\n", BTree_Height(tree));
printf("Degree: %d\n", BTree_Degree(tree));
printf("Count: %d\n", BTree_Count(tree));
// 显示清空后的二叉树
BTree_Display(tree, printf_data, 4, '-');
// 销毁二叉树
BTree_Destroy(tree);
return 0;
}
通过理解相关实现代码,我们发现通过指路法可以方便的定位二叉树中的结点,基于指路法的二叉树在插入,删除和获取操作的实现细节上与单链表相似。