程序员编程艺术：第一章、左旋转字符串

                   第一章、左旋转字符串

作者：July，yansha、caopengcs。
时间：二零一一年四月十四日。

 
题目描述：
定义字符串的左旋转操作：把字符串前面的若干个字符移动到字符串的尾部，如把字符串abcdef左旋转2位得到字符串cdefab。
请实现字符串左旋转的函数，要求对长度为n的字符串操作的时间复杂度为O(n)，空间复杂度为O(1)。 

思路一、暴力移位法

    初看此题，咱们最先想到的笨方法可能就是一位一位移动，故咱们写一个函数叫做 leftshiftone(char *s,int n) 完成左移动一位的功能

void leftshiftone(char *s,int n) {  
	char t = s[0];    //保存第一个字符  
	for (int i = 1; i < n; ++i) {  
		s[i - 1] = s[i];  
	}  
	s[n - 1] = t;  
}  

如此，左移m位的话，可以如下实现：

void leftshift(char *s,int n,int m) {  
	while (m--) {  
		leftshiftone(s, n);  
	}  
}  

思路二、指针翻转法

    咱们先来看个例子，如下：abc defghi，若要让abc移动至最后的过程可以是：abc defghi->def abcghi->def ghiabc

    如此，我们可定义俩指针，p1指向ch[0]，p2指向ch[m]；
一下过程循环m次，交换p1和p2所指元素，然后p1++, p2++；。

1. 第一步，交换abc 和def ，abc defghi->def abcghi
2. 第二步，交换abc 和 ghi，def abcghi->def ghiabc

    整个过程，看起来，就是abc 一步一步 向后移动

• abc defghi
• def abcghi
• def ghi abc  

  //最后的 复杂度是O（m+n）  

图解如下：

    由上述例子九个元素的序列abcdefghi，您已经看到，m=3时，p2恰好指到了数组最后一个元素，于是，上述思路没有问题。但如果上面例子中i 的后面还有元素列?

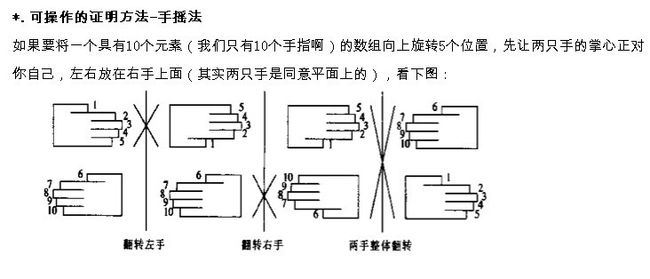
    即，如果是要左旋十个元素的序列：abcdefghij，ok，下面，就举这个例子，对abcdefghij序列进行左旋转操作：

如果abcdef ghij要变成defghij abc：
  abcdef ghij
1. def abc ghij
2. def ghi abc j      //接下来，j 步步前移
3. def ghi ab jc
4. def ghi a j bc
5. def ghi j abc 

 下面，再针对上述过程，画个图清晰说明下，如下所示：

  ok，咱们来好好彻底总结一下此思路二：（就4点，请仔细阅读）：

1、首先让p1=ch[0]，p2=ch[m]，即让p1，p2相隔m的距离；

2、判断p2+m-1是否越界，如果没有越界转到3，否则转到4（abcdefgh这8个字母的字符串，以4左旋，那么初始时p2指向e，p2+4越界了，但事实上p2至p2+m-1是m个字符，可以再做一个交换）。

3、不断交换*p1与*p2，然后p1++，p2++，循环m次，然后转到2。

4、此时p2+m-1 已经越界，在此只需处理尾巴。过程如下：

   4.1 通过n-p2得到p2与尾部之间元素个数r，即我们要前移的元素个数。

   4.2 以下过程执行r次：

       ch[p2]<->ch[p2-1]，ch[p2-1]<->ch[p2-2]，....，ch[p1+1]<->ch[p1]；p1++；p2++；

    所以，之前最初的那个左旋转九个元素abcdefghi的思路在末尾会出现问题的（如果p2后面有元素就不能这么变，例如，如果是处理十个元素，abcdefghij 列?对的，就是这个意思），解决办法有两个：

方法一（即如上述思路总结所述）：
def ghi abc jk
当p1指向a，p2指向j时，由于p2+m越界，那么此时p1，p2不要变
这里p1之后（abcjk)就是尾巴，处理尾巴只需将j,k移到abc之前，得到最终序列，代码编写如下：

//copyright@July、颜沙  
//最终代码，July，updated again，2011.04.17。  
#include   
#include   
using namespace std;  
  
void rotate(string &str, int m)  
{  
      
    if (str.length() == 0 || m <= 0)  
        return;  
      
    int n = str.length();  
      
    if (m % n <= 0)  
        return;  
      
    int p1 = 0, p2 = m;  
    int k = (n - m) - n % m;  
      
    // 交换p1，p2指向的元素，然后移动p1，p2  
    while (k --)   
    {  
        swap(str[p1], str[p2]);  
        p1++;  
        p2++;  
    }  
      
    // 重点，都在下述几行。  
    // 处理尾部，r为尾部左移次数  
    int r = n - p2;  
    while (r--)  
    {  
        int i = p2;  
        while (i > p1)  
        {  
            swap(str[i], str[i-1]);  
            i--;  
        }  
        p2++;  
        p1++;  
    }  
    //比如一个例子，abcdefghijk  
    //                    p1    p2  
    //当执行到这里时，defghi a b c j k  
    //p2+m出界 了，  
    //r=n-p2=2，所以以下过程，要执行循环俩次。  
      
    //第一次：j 步步前移，abcjk->abjck->ajbck->jabck  
    //然后，p1++，p2++，p1指a，p2指k。  
    //               p1    p2  
    //第二次：defghi j a b c k  
    //同理，此后，k步步前移，abck->abkc->akbc->kabc。  
}  
  
int main()     
{     
    string ch="abcdefghijk";     
    rotate(ch,3);     
    cout<

方法二：
def ghi abc jk
当p1指向a，p2指向j时，那么交换p1和p2，
此时为:
def ghi jbc ak

p1++，p2++,p1指向b，p2指向k，继续上面步骤得:
def ghi jkc ab

p1++，p2不动,p1指向c，p2指向b，p1和p2之间（cab)也就是尾巴，
那么处理尾巴（cab)需要循环左移一定次数（而后的具体操作步骤已在下述程序的注释中已详细给出）。

    根据方案二，不难写出下述代码（已测试正确）：

#include   
#include   
using namespace std;  
  
//颜沙，思路二之方案二，  
//July、updated，2011.04.16。  
void rotate(string &str, int m)  
{  
    if (str.length() == 0 || m < 0)  
        return;  
  
    //初始化p1，p2  
    int p1 = 0, p2 = m;     
    int n = str.length();  
  
    // 处理m大于n  
    if (m % n == 0)  
        return;  
      
    // 循环直至p2到达字符串末尾  
    while(true)  
    {    
        swap(str[p1], str[p2]);  
        p1++;  
        if (p2 < n - 1)  
            p2++;  
        else  
            break;  
    }  
      
    // 处理尾部，r为尾部循环左移次数  
    int r = m - n % m;  // r = 1.  
    while (r--)  //外循环执行一次  
    {  
        int i = p1;  
        char temp = str[p1];  
        while (i < p2)  //内循环执行俩次  
        {  
            str[i] = str[i+1];  
            i++;  
        }     
        str[p2] = temp;  
    }  
    //举一个例子  
    //abcdefghijk  
    //当执行到这里的时候，defghiabcjk  
    //      p1    p2  
    //defghi a b c j k，a 与 j交换，jbcak，然后，p1++，p2++  
    //        p1    p2  
    //       j b c a k，b 与 k交换，jkcab，然后，p1++，p2不动，  
      
    //r = m - n % m= 3-11%3=1，即循环移位1次。  
    //          p1  p2  
    //       j k c a b  
    //p1所指元素c实现保存在temp里，  
    //然后执行此条语句：str[i] = str[i+1]; 即a跑到c的位置处，a_b  
    //i++，再次执行：str[i] = str[i+1]，ab_  
    //最后，保存好的c 填入，为abc，所以，最终序列为defghi jk abc。  
    //July、updated，2011.04.17晚，送走了她。  
}  
  
int main()  
{  
    string ch="abcdefghijk";  
    rotate(ch,3);  
    cout<

注意：上文中都是假设m

还可以看下这段代码：

/* 
 * myinvert2.cpp 
 * 
 *  Created on: 2011-5-11 
 *      Author: BigPotato 
 */  
#include  
#include  
#define positiveMod(m,n) ((m) % (n) + (n)) % (n)  
  
/* 
 *左旋字符串str，m为负数时表示右旋abs（m）个字母 
 */  
void rotate(std::string &str, int m) {  
    if (str.length() == 0)  
        return;  
    int n = str.length();  
    //处理大于str长度及m为负数的情况,positiveMod可以取得m为负数时对n取余得到正数  
    m = positiveMod(m,n);  
    if (m == 0)  
        return;  
    //    if (m % n <= 0)  
    //        return;  
    int p1 = 0, p2 = m;  
    int round;  
    //p2当前所指和之后的m-1个字母共m个字母，就可以和p2前面的m个字母交换。  
    while (p2 + m - 1 < n) {  
        round = m;  
        while (round--) {  
            std::swap(str[p1], str[p2]);  
            p1++;  
            p2++;  
        }  
    }  
    //剩下的不足m个字母逐个交换  
    int r = n - p2;  
    while (r--) {  
        int i = p2;  
        while (i > p1) {  
            std::swap(str[i], str[i - 1]);  
            i--;  
        }  
        p2++;  
        p1++;  
    }  
}  
  
//测试  
int main(int argc, char **argv) {  
    //    std::cout << ((-15) % 7 + 7) % 7 << std::endl;  
    //    std::cout << (-15) % 7 << std::endl;  
    std::string ch = "abcdefg";  
    int len = ch.length();  
    for (int m = -2 * len; m <= len * 2; m++) {  
        //由于传给rotate的是string的引用，所以这里每次调用都用了一个新的字符串  
        std::string s = "abcdefg";  
        rotate(s, m);  
        std::cout << positiveMod(m,len) << ": " << s << std::endl;  
    }  
   
    return 0;  
} 

思路三、递归转换法

    本文最初发布时，网友留言bluesmic说：楼主，谢谢你提出的研讨主题，很有学术和实践价值。关于思路二，本人提一个建议：思路二的代码，如果用递归的思想去简化，无论代码还是逻辑都会更加简单明了。

    就是说，把一个规模为N的问题化解为规模为M(M    举例来说，设字符串总长度为L，左侧要旋转的部分长度为s1，那么当从左向右循环交换长度为s1的小段，直到最后，由于剩余的部分长度为s2(s2==L%s1)而不能直接交换。

    该问题可以递归转化成规模为s1+s2的，方向相反(从右向左)的同一个问题。随着递归的进行，左右反复回荡，直到某一次满足条件L%s1==0而交换结束。

     举例解释一下：
    设原始问题为：将“123abcdefg”左旋转为“abcdefg123”，即总长度为10，旋转部("123")长度为3的左旋转。按照思路二的运算，演变过程为“123abcdefg”->"abc123defg"->"abcdef123g"。这时，"123"无法和"g"作对调，该问题递归转化为：将“123g”右旋转为"g123"，即总长度为4，旋转部("g")长度为1的右旋转。

updated：

Ys：

Bluesmic的思路没有问题，他的思路以前很少有人提出。思路是通过递归将问题规模变小。当字符串总长度为n，左侧要旋转的部分长度为m，那么当从左向右循环交换长度为m的小段直到剩余部分为m’(n % m)，此时m’ < m，已不能直接交换了。

此后，我们换一个思路，把该问题递归转化成规模大小为m’ +m，方向相反的同一问题。随着递归的进行，直到满足结束条件n % m==0。

 

  举个具体事例说明，如下：

1、对于字符串abc def ghi gk，

将abc右移到def ghi gk后面，此时n = 11，m = 3，m’ = n % m = 2;

abc def ghi gk -> def ghi abc gk

2、问题变成gk左移到abc前面，此时n = m’ + m = 5，m = 2，m’ = n % m 1;

abc gk -> a gk bc

3、问题变成a右移到gk后面，此时n = m’ + m = 3，m = 1，m’ = n % m = 0;

a gk bc-> gk a bc。 由于此刻，n % m = 0，满足结束条件，返回结果。

 

    即从左至右，后从右至左，再从左至右，如此反反复复，直到满足条件，返回退出。

    代码如下，已测试正确（有待优化）：

//递归，  
//感谢网友Bluesmic提供的思路  
  
//copyright@ yansha 2011.04.19  
//July，updated，2011.04.20.  
#include   
using namespace std;  
  
void rotate(string &str, int n, int m, int head, int tail, bool flag)  
{  
    //n 待处理部分的字符串长度，m：待处理部分的旋转长度  
    //head：待处理部分的头指针，tail：待处理部分的尾指针  
    //flag = true进行左旋，flag = false进行右旋  
      
    // 返回条件  
    if (head == tail || m <= 0)  
        return;  
      
    if (flag == true)  
    {  
        int p1 = head;  
        int p2 = head + m;  //初始化p1，p2  
          
        //1、左旋：对于字符串abc def ghi gk，  
        //将abc右移到def ghi gk后面，此时n = 11，m = 3，m’ = n % m = 2;  
        //abc def ghi gk -> def ghi abc gk  
        //（相信，经过上文中那么多繁杂的叙述，此类的转换过程，你应该是了如指掌了。）  
          
        int k = (n - m) - n % m;   //p1，p2移动距离，向右移六步  
  
        /*--------------------- 
        解释下上面的k = (n - m) - n % m的由来： 
        yansha： 
        以p2为移动的参照系： 
        n-m 是开始时p2到末尾的长度，n%m是尾巴长度 
        (n-m)-n%m就是p2移动的距离 
        比如 abc def efg hi 
        开始时p2->d,那么n-m 为def efg hi的长度8， 
        n%m 为尾巴hi的长度2， 
        因为我知道abc要移动到hi的前面，所以移动长度是 
        (n-m)-n%m = 8-2 = 6。 
        */  
          
        for (int i = 0; i < k; i++, p1++, p2++)  
            swap(str[p1], str[p2]);  
          
        rotate(str, n - k, n % m, p1, tail, false);  //flag标志变为false，结束左旋，下面，进入右旋  
    }  
    else  
    {  
        //2、右旋：问题变成gk左移到abc前面，此时n = m’ + m = 5，m = 2，m’ = n % m 1;  
        //abc gk -> a gk bc  
          
        int p1 = tail;  
        int p2 = tail - m;  
          
        // p1，p2移动距离，向左移俩步  
        int k = (n - m) - n % m;  
          
        for (int i = 0; i < k; i++, p1--, p2--)  
            swap(str[p1], str[p2]);  
          
        rotate(str, n - k, n % m, head, p1, true);  //再次进入上面的左旋部分，  
        //3、左旋：问题变成a右移到gk后面，此时n = m’ + m = 3，m = 1，m’ = n % m = 0;  
        //a gk bc-> gk a bc。 由于此刻，n % m = 0，满足结束条件，返回结果。  
  
    }  
}  
  
int main()  
{  
    int i=3;  
    string str = "abcdefghijk";  
    int len = str.length();  
    rotate(str, len, i % len, 0, len - 1, true);  
    cout << str.c_str() << endl;   //转化成字符数组的形式输出  
    return 0;  
}  

非常感谢。

    稍后，由下文，您将看到，其实上述思路二的本质即是下文将要阐述的stl rotate算法，详情，请继续往下阅读。

 

思路四、循环移位法

    下面，我将再具体深入阐述下此STL 里的rotate算法，由于stl里的rotate算法，用到了gcd的原理，下面，我将 先介绍辗转相除法(又称欧几里得算法、gcd算法）的算法思路及原理。

    gcd，即辗转相除法，又称欧几里得算法，是求最大公约数的算法，即求两个正整数之最大公因子的算法。此算法作为TAOCP第一个算法被阐述，足见此算法被重视的程度。

    gcd算法：给定俩个正整数m，n（m>=n），求它们的最大公约数。（注意，一般要求m>=n，若mn。下文，会具体解释）。

    用数学定理表示即为：“定理：gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不为0)”。以下，是此算法的具体流程：
    1、[求余数]，令r=m%n，r为n除m所得余数（0<=r    2、[余数为0?]，若r=0，算法结束，此刻，n即为所求答案，否则，继续，转到3；
    3、[重置]，置m<-n，n<-r，返回步骤1.

    此算法的证明，可参考计算机程序设计艺术第一卷：基本算法。证明，此处略。

    ok，下面，举一个例子，你可能看的更明朗点。
    比如，给定m=544，n=119，
      则余数r=m%n=544%119=68; 因r!=0，所以跳过上述步骤2，执行步骤3。；
      置m<-119，n<-68，=>r=m%n=119%68=51;
      置m<-68，n<-51，=>r=m%n=68%51=17；
      置m<-51，n<-17，=>r=m%n=51%17=0，算法结束，

    此时的n=17，即为m=544，n=119所求的俩个数的最大公约数。

    再解释下上述gcd(m，n)算法开头处的，要求m>=n 的原因：举这样一个例子，如m    因为r!=0,所以执行上述步骤3，注意，看清楚了：m<-544，n<-119。看到了没，尽管刚开始给的m=n。

    ok，我想，现在，你已经彻底明白了此gcd算法，下面，咱们进入主题，stl里的rotate算法的具体实现。//待续。

    熟悉stl里的rotate算法的人知道，对长度为n的数组(ab)左移m位，可以用stl的rotate函数（stl针对三种不同的迭代器，提供了三个版本的rotate）。但在某些情况下，用stl的rotate效率极差。

    对数组循环移位，可以采用的方法有（也算是对上文思路一，和思路二的总结）：

      flyinghearts：
      ① 动态分配一个同样长度的数组，将数据复制到该数组并改变次序，再复制回原数组。（最最普通的方法）
      ② 利用ba=(br)^T(ar)^T=(arbr)^T，通过三次反转字符串。（即上述思路一，首先对序列前部分逆序，再对序列后部分逆序，再对整个序列全部逆序）
      ③ 分组交换（尽可能使数组的前面连续几个数为所要结果）：
      若a长度大于b，将ab分成a0a1b，交换a0和b，得ba1a0，只需再交换a1 和a0。
      若a长度小于b，将ab分成ab0b1，交换a和b0，得b0ab1，只需再交换a 和b0。
      通过不断将数组划分，和交换，直到不能再划分为止。分组过程与求最大公约数很相似。
      ④ 所有序号为 (j+i *m) % n (j 表示每个循环链起始位置，i 为计数变量，m表示左旋转位数，n表示字符串长度)，会构成一个循环链（共有gcd(n,m)个，gcd为n、m的最大公约数），每个循环链上的元素只要移动一个位置即可，最后整个过程总共交换了n次（每一次循环链，是交换n/gcd(n,m)次，总共gcd(n,m)个循环链。所以，总共交换n次）。

    stl的rotate的三种迭代器，即是，分别采用了后三种方法。

    在给出stl rotate的源码之前，先来看下我的朋友ys对上述第4种方法的评论：
    ys：这条思路个人认为绝妙，也正好说明了数学对算法的重要影响。

    通过前面思路的阐述，我们知道对于循环移位，最重要的是指针所指单元不能重复。例如要使abcd循环移位变成dabc(这里m=3,n=4)，经过以下一系列眼花缭乱的赋值过程就可以实现：
    ch[0]->temp, ch[3]->ch[0], ch[2]->ch[3], ch[1]->ch[2], temp->ch[1];  （*）
    字符串变化为：abcd->_bcd->dbc_->db_c->d_bc->dabc;
是不是很神奇？其实这是有规律可循的。

    请先看下面的说明再回过头来看。
 对于左旋转字符串，我们知道每个单元都需要且只需要赋值一次，什么样的序列能保证每个单元都只赋值一次呢？

      1、对于正整数m、n互为质数的情况，通过以下过程得到序列的满足上面的要求：
 for i = 0: n-1
      k = i * m % n;
 end

    举个例子来说明一下，例如对于m=3,n=4的情况，
        1、我们得到的序列：即通过上述式子求出来的k序列，是0, 3, 2, 1。
        2、然后，你只要只需按这个顺序赋值一遍就达到左旋3的目的了：
    ch[0]->temp, ch[3]->ch[0], ch[2]->ch[3], ch[1]->ch[2], temp->ch[1];   （*） 

    ok，这是不是就是按上面（*）式子的顺序所依次赋值的序列阿?哈哈，很巧妙吧。当然，以上只是特例，作为一个循环链，相当于rotate算法的一次内循环。

     2、对于正整数m、n不是互为质数的情况（因为不可能所有的m，n都是互质整数对），那么我们把它分成一个个互不影响的循环链，正如flyinghearts所言，所有序号为 (j + i * m) % n（j为0到gcd(n, m)-1之间的某一整数，i = 0:n-1）会构成一个循环链，一共有gcd(n, m)个循环链，对每个循环链分别进行一次内循环就行了。

    综合上述两种情况，可简单编写代码如下：

//④ 所有序号为 (j+i *m) % n (j 表示每个循环链起始位置，i 为计数变量，m表示左旋转位数，n表示字符串长度)， //会构成一个循环链（共有gcd(n,m)个，gcd为n、m的最大公约数）， //每个循环链上的元素只要移动一个位置即可，最后整个过程总共交换了n次 //（每一次循环链，是交换n/gcd(n,m)次，共有gcd(n,m)个循环链，所以，总共交换n次）。 void rotate(string &str, int m) { int lenOfStr = str.length(); int numOfGroup = gcd(lenOfStr, m); int elemInSub = lenOfStr / numOfGroup; for(int j = 0; j < numOfGroup; j++) //对应上面的文字描述，外循环次数j为循环链的个数，即gcd(n, m)个循环链 { char tmp = str[j]; for (int i = 0; i < elemInSub - 1; i++) //内循环次数i为，每个循环链上的元素个数，n/gcd(m,n)次 str[(j + i * m) % lenOfStr] = str[(j + (i + 1) * m) % lenOfStr]; str[(j + i * m) % lenOfStr] = tmp; } }

后来有网友针对上述的思路④，给出了下述的证明：
    1、首先，直观的看肯定是有循环链，关键是有几条以及每条有多长，根据(i+j *m) % n这个表达式可以推出一些东东，一个j对应一条循环链，现在要证明(i+j *m) % n有n/gcd(n,m)个不同的数。
    2、假设j和k对应的数字是相同的， 即(i+j*m)%n = (i+k*m)%n， 可以推出n|(j-k)*m，m=m’*gcd(n.m), n=n’*gcd(n,m), 可以推出n’|(j-k)*m’，而m’和n’互素，于是n’|(j-k)，即(n/gcd(n,m))|(j-k)，
    3、所以(i+j*m) % n有n/gcd(n,m)个不同的数。则总共有gcd(n，m)个循环链。符号“|”是整除的意思。
以上的3点关于为什么一共有gcd(n, m)个循环链的证明，应该是来自qq3128739xx的，非常感谢这位朋友。

由于上述stl rotate源码中，方案④ 的代码，较复杂，难以阅读，下面是对上述第④ 方案的简单改写：

//对上述方案4的改写。  
//④ 所有序号为 (i+t*k) % n (i为指定整数，t为任意整数)，....  
//copyright@ hplonline && July 2011.04.18。  
//July、sahala、yansha，updated，2011.06.02。  
void my_rotate(char *begin, char *mid, char *end)  
{     
    int n = end - begin;     
    int k = mid - begin;     
    int d = gcd(n, k);     
    int i, j;     
    for (i = 0; i < d; i ++)     
    {     
        int tmp = begin[i];     
        int last = i;     
          
        //i+k为i右移k的位置，%n是当i+k>n时从左重新开始。  
        for (j = (i + k) % n; j != i; j = (j + k) % n)    //多谢laocpp指正。     
        {     
            begin[last] = begin[j];         
            last = j;     
        }         
        begin[last] = tmp;     
    }     
}   

    对上述程序的解释：关于第二个for循环中，j初始化为（i+k）%n，程序注释中已经说了，i+k为i右移k的位置，%n是当i+k>n时从左重新开始。为什么要这么做呢?很简单，n个数的数组不管循环左移多少位，用上述程序的方法一共需要交换n次。当i+k>=n时i+k表示的位置在数组中不存在了，所以又从左边开始的(i+k)%n是下一个交换的位置。

1. 好比5个学生,，编号从0开始，即0 1 2 3 4，老师说报数，规则是从第一个学生开始，中间隔一个学生报数。报数的学生编号肯定是0 2 4 1 3。这里就相当于i为0，k为2，n为5；
2. 然后老师又说，编号为0的学生出列，其他学生到在他前一个报数的学生位置上去，那么学生从0 1 2 3 4=》2 3 4 _ 1，最后老师说，编号0到剩余空位去，得到最终排位2 3 4 0 1。此时的结果，实际上就是相当于上述程序中左移k=2个位置了。而至于为什么让 编号为0 的学生 出列。实际是这句：int last = i; 因为要达到这样的效果0 1 2 3 4 => 2 3 4 0 1，那么2 3 4 必须要移到前面去。怎么样，明白了么?。

关于本题，不少网友也给出了他们的意见，具体请参见此帖子微软100题，维护地址。 

思路五、三步翻转法

    对于这个问题，咱们换一个角度，可以这么做：

将一个字符串分成两部分，X和Y两个部分，在字符串上定义反转的操作X^T，即把X的所有字符反转（如，X="abc"，那么X^T="cba"），那么我们可以得到下面的结论：(X^TY^T)^T=YX。显然我们这就可以转化为字符串的反转的问题了。

不是么?ok,就拿abcdef 这个例子来说，若要让def翻转到abc的前头，那么只要按下述3个步骤操作即可：
1、首先分为俩部分，X:abc，Y:def；
2、X->X^T，abc->cba， Y->Y^T，def->fed。
3、(X^TY^T)^T=YX，cbafed->defabc，即整个翻转。

我想，这下，你应该一目了然了。

    其次，在《编程珠玑》上也有这样一个类似的问题，它的解法同本思路一致，如下图所示：

然后，代码可以这么写：

//Copyright@ 小桥流水 && July  
//c代码实现，已测试正确。  
//http://www.smallbridge.co.cc/2011/03/13/100%E9%A2%98  
//_21-%E5%B7%A6%E6%97%8B%E8%BD%AC%E5%AD%97%E7%AC%A6%E4%B8%B2.html  
//July、updated，2011.04.17。  
char * invert(char *start, char *end)  
{     
	char tmp, *ptmp = start;      
	while (start != NULL && end != NULL && start < end)    
	{     
		tmp = *start;     
		*start = *end;        
		*end = tmp;       
		start ++;     
		end --;   
	}  
	return ptmp;  
}  

char *left(char *s, int pos)   //pos为要旋转的字符个数，或长度，下面主函数测试中，pos=3。  
{  
	int len = strlen(s);  
	invert(s, s + (pos - 1));  //如上，X->X^T，即 abc->cba  
	invert(s + pos, s + (len - 1)); //如上，Y->Y^T，即 def->fed  
	invert(s, s + (len - 1));  //如上，整个翻转，(X^TY^T)^T=YX，即 cbafed->defabc。  
	return s;  
}  

完。