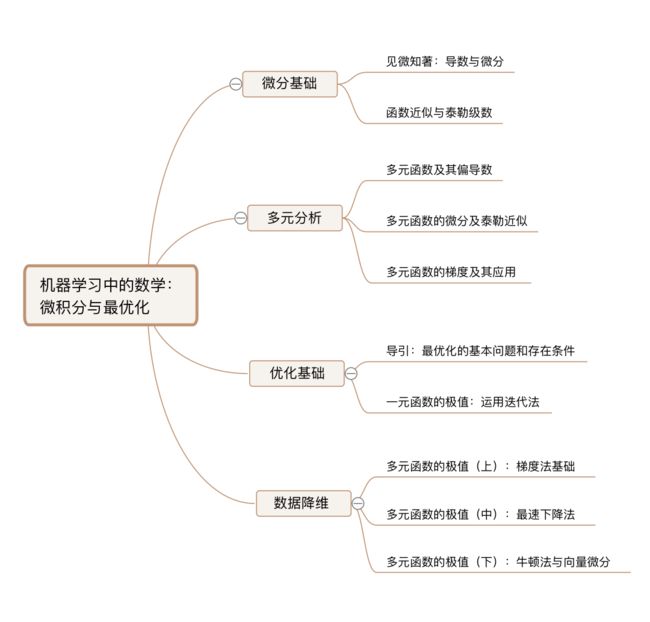
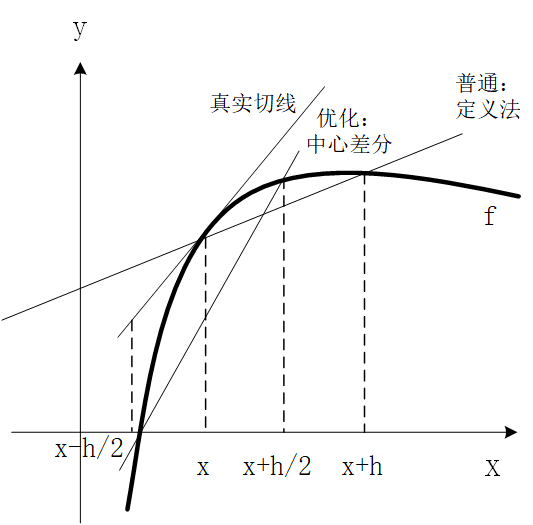机器学习中的数学：微积分与最优化

专栏亮点

• 篇幅短小精悍，帮你提炼重点：这不是一个大而全的高等数学课程，而是一个简明扼要的专栏，解决的是机器学习中最优化问题所需要的核心基础概念，但对于最重要的微分基础、多元分析、优化基础和多元极值四部分知识，我们则进行庖丁解牛式的透彻讲解。
• 使用 Python 工具，无缝对接工程：教你用熟、用好 NumPy、SciPy、Matplotlib、Pandas 等工具库，无缝对接工程实践应用。
• 结合优化算法，提升学习效率： 结合实际的典型优化算法，分析、讲解微积分内容，通过更强的导向性和目标性，大幅度提升学习效率。

为什么要学习微积分？

机器学习是一个综合性强、知识栈长的学科，需要大量的前序知识作为铺垫，绝大多数算法模型和实际应用都依赖于以概率统计、线性代数和微积分为代表的数学基础。

《机器学习里的数学》系列的第三季，我们开始讨论机器学习里的微积分与最优化。

• 《机器学习中的数学 I：概率统计》
• 《机器学习中的数学 II：线性代数》
• 《机器学习中的数学 III：微积分与最优化》

微积分与最优化，是机器学习模型中问题最终解决方案的落地手段。当我们分析具体问题，并建立好算法模型后，问题的最终求解过程往往都会涉及到优化问题，因此我们需要去探寻数据空间中的极值。这一切如果没有微分理论和计算方法作为支撑，任何漂亮的模型都无法落地。因此夯实多元微分的基本概念，掌握最优化的实现方法，是通往问题最终解决方案的必经之路。

在机器学习的实践中，对于一个函数，尤其是多元函数而言，读者需要面对许多非常重要的概念和方法问题：

• 我们常说的导数和微分的背后的几何含义是什么？我们常常听说的链式法则又是如何运转的？
• 对于一个连续的函数，我们是如何基于不同阶数的导数，在指定点处，利用有限的级数项之和对函数进行近似？
• 多元函数中的梯度指示出了怎样的重要信息？我们如何利用它去寻找函数的极值？
• 利用程序进行函数极值求解时，如何利用不断迭代的方法在连续的函数中实现我们的目标？
• 梯度法、最速下降法、牛顿法，这些极值求解的具体方法是如何实现的？各有什么优点和不足？

这些微积分中的重要问题和概念，是理解和实现优化方法的重中之重。

因此，在《机器学习中的数学：微积分与最优化》中，我们将重点落实微分基础、多元分析、优化基础和多元极值这四部分内容，一次讲清楚优化算法中最为关键的基本概念和方法。

专栏大纲

我们将通过专栏的四大核心板块向你依次展现机器学习所需的微积分核心内容。

第 1 部分：微分基础。这一部分从一元函数的导数和微分入手，快速理清连续与可微、切线与导数等重要概念，巩固核心基础，同时从切线的几何意义出发顺势引出微分的数值求法。在此基础上进一步讨论一元函数的泰勒近似，引导读者利用高阶导数基于有限的级数项，在指定点对函数进行近似处理。

第 2 部分：多元分析。这一部分由一元过渡到多元函数，导数与微分的概念得以进一步完善和深化，引出多元函数的极限、连续以及偏导数，并在多元微分的几何意义的基础上，讨论了多元函数的泰勒近似。同时从偏导数的几何意义出发，引出这一部分最为重要的概念：多元函数的梯度向量和黑塞矩阵，探究梯度与函数值变化的重要关系，为后面的优化方法打好基础。

第 3 部分：优化基础。这一部分讨论了最优化的概念基础，首先我们分析最优化问题的由来和背景，然后重点讨论函数极值存在的条件以及探索函数极值过程中常用的迭代法。

第 4 部分：多元极值。这一部分面向几个典型的实际算法，分别举了多元函数极值求取的一阶方法和二阶方法的典型例子，对许多材料中耳熟能详、反复出现的梯度法、最速下降法以及牛顿法都进行了深入的介绍和完整的实现。同时综合整个四部分内容，整合微分与优化的完整知识闭环。

作者介绍

适宜人群

• 对人工智能感兴趣的开发者
• 想入门机器学习的初学者
• 想加强数学基本功的读者

购买须知

• 本专栏为图文内容，共计 11 篇。
• 每周二、四更新，预计于 2020 年 1 月 2 日更新完毕。
• 付费用户可享受文章永久阅读权限。
• 本专栏为虚拟产品，一经付费概不退款，敬请谅解。
• 本专栏可在 GitChat 服务号、App 及网页端 gitbook.cn 上购买，一端购买，多端阅读。

订阅福利

• 本专栏限时特价 12.9 元，12 月 19 日恢复至原价 19 元。
• 订购本专栏可获得专属海报（在 GitChat 服务号领取），分享专属海报每成功邀请一位好友购买，即可获得 25% 的返现奖励，多邀多得，上不封顶，立即提现。
• 提现流程：在 GitChat 服务号中点击「我-我的邀请-提现」。
• 购买本专栏后，可加入读者群交流（入群方式可查看第 3 篇文末说明）。

课程内容

微积分与最优化：最终解决方案的落地手段

机器学习中，数学为什么重要？

大家好，我是张雨萌，毕业于清华大学计算机系，目前从事自然语言处理相关的研究工作。撰写《机器学习中的数学》系列专栏并和大家一起共同交流学习，是我们准备了很久的一个计划。

当下，机器学习、人工智能领域吸引了许多有志者投身其中，其中包含了大量非科班出身或从其他行业切换赛道转行而来的朋友。大家在学习的过程中经常会感觉学习曲线陡峭、难度较大，而机器学习之所以这么难，首要原因就是数学知识需要得太多了！

的确如此，机器学习是一个综合性强、知识栈长的学科，需要大量的前序知识作为铺垫。其中最核心的就是：绝大多数算法模型和实际应用都依赖于以概率统计、线性代数和微积分为代表的数学理论和思想方法。

比方说吧，如果你想对高维数据进行降维分析，提取和聚焦其主成分，需要的就是线性代数中空间的概念和矩阵分解的技巧；想理解神经网络的训练过程，离不开多元微分和优化方法；想过滤垃圾邮件，不具备概率论中的贝叶斯思维恐怕不行；想试着进行一段语音识别，则必须要理解随机过程中的隐马尔科夫模型；想通过一个数据样本集推测出这类对象的总体特征，统计学中的估计理论和大数定理的思想必须得建立。因此，数学基础是机器学习绕不开的重要阵地。

机器学习中，三部分数学知识各自扮演什么角色？

针对这三部分内容，我们在近期依次推出了 《机器学习中的数学：概率统计》、 《机器学习中的数学：线性代数》 和 《机器学习中的数学：微积分与最优化》 三个专栏。

在进入到微积分与最优化这部分之前，我们先来看看这三部分数学知识在机器学习中各自扮演着什么样的角色，并梳理一下学科的内在逻辑。

第一：概率统计是利用数据发现规律、推测未知的思想方法

「发现规律、推测未知」也正是机器学习的目标，所以两者的目标高度一致。机器学习中的思想方法和核心算法大多构筑在统计思维方法之上。本专栏介绍的核心概率思想和基础概念将围绕着条件概率、随机变量、随机过程、极限思想、统计推断、概率图等内容展开。

第二：线性代数是利用空间投射和表征数据的基本工具

通过线性代数，我们可以灵活地对数据进行各种变换，从而直观清晰地挖掘出数据的主要特征和不同维度的信息。整个线性代数的主干就是空间变换，我们将从构筑空间、近似拟合、相似矩阵、数据降维这四大板块，环环相扣地呈现出与机器学习算法紧密相关的最核心内容。

第三：微积分与最优化是机器学习模型中最终解决方案的落地手段

当我们建立好算法模型之后，问题的最终求解往往都会涉及到优化问题。在探寻数据空间极值的过程中，如果没有微分理论和计算方法作为支撑，任何漂亮的模型都无法落地。因此，夯实多元微分的基本概念，掌握最优化的实现方法，是通向最终解决方案的必经之路。

微积分与最优化有什么用？

作为《机器学习里的数学》系列的第三季，我们开始讨论机器学习里的微积分与最优化。

微积分与最优化，是机器学习模型中问题最终解决方案的落地手段。当我们分析具体问题，并建立好算法模型后，问题的最终求解过程往往都会涉及到优化问题，因此我们需要去探寻数据空间中的极值。这一切如果没有微分理论和计算方法作为支撑，任何漂亮的模型都无法落地。因此夯实多元微分的基本概念，掌握最优化的实现方法，是通往问题最终解决方案的必经之路。

在机器学习的实践中，对于一个函数，尤其是多元函数而言，读者需要面对许多非常重要的概念和方法问题：

• 我们常说的导数和微分的背后的几何含义是什么？我们常常听说的链式法则又是如何运转的？
• 对于一个连续的函数，我们是如何基于不同阶数的导数，在指定点处，利用有限的级数项之和对函数进行近似？
• 多元函数中的梯度指示出了怎样的重要信息？我们如何利用它去寻找函数的极值？
• 利用程序进行函数极值求解时，如何利用不断迭代的方法在连续的函数中实现我们的目标？
• 梯度法、最速下降法、牛顿法，这些极值求解的具体方法是如何实现的？各有什么优点和不足？

这些微积分中的重要问题和概念，是理解和实现优化方法的重中之重。

因此，在《机器学习中的数学：微积分与最优化》中，我们将重点落实微分基础、多元分析、优化基础和多元极值这四部分内容，一次讲清楚优化算法中最为关键的基本概念和方法。

专栏的亮点和特色

• 篇幅短小精悍，帮你提炼重点：这不是一个大而全的高等数学课程，而是一个简明扼要的专栏，解决的是机器学习中最优化问题所需要的核心基础概念，但对于最重要的微分基础、多元分析、优化基础和多元极值四部分知识，我们则进行庖丁解牛式的透彻讲解。
• 使用 Python 工具，无缝对接工程：教你用熟、用好 NumPy、SciPy、Matplotlib、Pandas 等工具库，无缝对接工程实践应用。
• 结合优化算法，提升学习效率： 结合实际的典型优化算法，分析、讲解微积分内容，通过更强的导向性和目标性，大幅度提升学习效率。

设计思路

我们将通过专栏的四大核心板块向你依次展现机器学习所需的微积分核心内容。

第 1 部分：微分基础。这一部分从一元函数的导数和微分入手，快速理清连续与可微、切线与导数等重要概念，巩固核心基础，同时从切线的几何意义出发顺势引出微分的数值求法。在此基础上进一步讨论一元函数的泰勒近似，引导读者利用高阶导数基于有限的级数项，在指定点对函数进行近似处理。

第 2 部分：多元分析。这一部分由一元过渡到多元函数，导数与微分的概念得以进一步完善和深化，引出多元函数的极限、连续以及偏导数，并在多元微分的几何意义的基础上，讨论了多元函数的泰勒近似。同时从偏导数的几何意义出发，引出这一部分最为重要的概念：多元函数的梯度向量和黑塞矩阵，探究梯度与函数值变化的重要关系，为后面的优化方法打好基础。

第 3 部分：优化基础。这一部分讨论了最优化的概念基础，首先我们分析最优化问题的由来和背景，然后重点讨论函数极值存在的条件以及探索函数极值过程中常用的迭代法。

第 4 部分：多元极值。这一部分面向几个典型的实际算法，分别举了多元函数极值求取的一阶方法和二阶方法的典型例子，对许多材料中耳熟能详、反复出现的梯度法、最速下降法以及牛顿法都进行了深入的介绍和完整的实现。同时综合整个四部分内容，整合微分与优化的完整知识闭环。

让我们一起开始这段学习旅程！

万丈高楼平地起，希望《机器学习中的数学》系列专栏能陪伴大家走好机器学习的学习与实践的必经之路、梳理纷繁复杂的知识网络、构筑好算法模型的数学基础。更重要的是，我希望我们能一起形成一种思维习惯：源于理论，我们条分缕析；面向实践，我们学以致用。 有了扎实的数学理论和方法基础，相信同学们都能登高望远、一往无前。

分享交流

我们为本专栏付费读者创建了微信交流群，以便更有针对性地讨论专栏相关的问题（入群方式请在第 3 篇末尾查看）。

见微知著：导数与微分

函数的连续性

函数在单点处的连续性

从这一讲开始，我们正式进入到微积分的部分中来。我们首先从函数的连续性开始讨论，然后逐步过渡到切线和导数的概念。

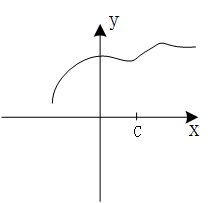
函数 f(x) 在具体的取值点 c 点是否连续，我们针对性地来看下面三幅图中的具体情形：

在这幅图中，我们发现在点 c 处，函数的左极限和右极限不相等，即

$$lim{x\rightarrow c^{-}}f(x) \neq lim{x\rightarrow c^{+}}f(x)$$

因此 $lim_{x\rightarrow c}f(x)$ 不存在，c 点处函数的极限不存在，因此函数 f(x) 在点 c 处不连续。

这幅图中情况似乎要稍微好点儿，我们发现

$$lim{x\rightarrow c^{-}}f(x)=lim{x\rightarrow c^{+}}f(x)$$

函数 f(x) 在 c 点处的极限是存在的，但是从图中可以看出，函数的极限值和 c 点处函数的实际取值不相等，即：

$$lim_{x\rightarrow c}f(x) \neq f(c)$$

因此函数 f(x) 在点 c 处仍然不连续。

这幅图中以上出现的两个问题都不存在了，我们看到：一方面函数 f(x) 的极限是存在的，而另一方面 $lim_{x\rightarrow c}f(x)=f(c)$，点 c 处的极限和函数的取值又是相等的，因此在这幅图中，函数 f(x) 在点 c 处是连续的。

那么，依照严格的定义，对于一个定义在包含点 c 的区间上的函数 f(x)，如果 $lim_{x\rightarrow c}f(x)=f(c)$ 成立，则称函数 f 在点 c 处连续。

函数在区间上的连续性

进一步扩展到区间上，如果函数 f(x) 在开区间上的任意一点连续，那么这个函数 f(x) 就在整个这个开区间上连续。

如果谈到闭区间 [a,b] 上的连续性问题，那么就需要着重单独讨论区间的左右两个端点：我们首先从右侧逼近左侧端点 a，如果 $lim{x\rightarrow a^{+}}f(x) =f(a)$ 成立，则称函数 f(x) 在端点 a 上右连续，我们再从左侧逼近右侧端点 b，即 $lim{x\rightarrow b^{-}}f(x) =f(b)$ 成立，则称函数 f(x) 在端点 b 上右连续。

那么，如果函数在开区间 (a,b) 上连续，且在左侧端点 a 上右连续，在右侧端点 b 上左连续，此时此刻，我们就能够说函数 f(x) 在闭区间 [a,b] 上是连续的。

关于切线

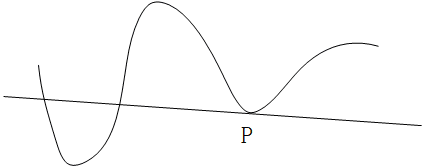
切线是一个大家都非常熟悉的概念，什么是切线？有一种说法是，一条曲线的切线只与这条曲线有一个交点。这个概念有很大的局限性，它只对圆环类的曲线有效，而对例如下面的这条曲线，描述显然就不适用了：

实际上，在上面这幅图中，直线显然是曲线在 P 点处的切线，但是更明显的是，这条直线与曲线的交点数不止一个。那么我们应该怎样更准确地描述切线呢？这里就要用到极限的概念。

我们还是看曲线上 P 点的切线：我们假定 Q 点为曲线上一个接近 P 点的可动点，经过 P 点和 Q 点的直线叫做割线，在 P 点的切线就是当 Q 点沿曲线向 P 点移动时，割线的极限位置，如下图所示：

因此，结合上面这幅图，我们来总结一下切线的严格定义：

已知的任意一条曲线 y=f(x) 在点 P(c,f(c)) 处的切线就是穿过该点 P 的一条直线，且这条直线的斜率为：

$$lim_{h\rightarrow 0} \frac{f(c+h)-f(c)}{h}$$

当然，这里有个前提条件，那就是表示斜率的这个极限存在且不为 $\infty$ 或 $-\infty$。

导数的介绍

从切线到导数

切线的概念很简单，我们也非常熟悉，这里我们不做过多停留。下面我们进入到导数概念的介绍，导数的定义和斜率其实看上去很像。

函数 f 的导数我们将其记作 f'，其实它是另外一个函数，导数对定义域内任意自变量 x 的函数值为：

$$f'(x)=lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$$

如果这个极限存在，那么我们就说函数 f 在 x 点处可微，而这个求导的过程就叫作微分。

当然，导数的定义式还有另一种等价的形式：

$$f'(c)=lim_{x\rightarrow c}\frac{f(x)-f(c)}{x-c}$$

可微一定连续

这短短的定义式里，其实有很多坑等着我们，最主要的就是分析可微和连续之间的关系。

首先，可微性一定能够推出连续性，说具体点就是：如果函数的导数 f'(c) 存在，那么函数 f 在点 c 处就是连续的。这个概念我们简单推导一下，大家就能够明白了。

首先对函数 f(x) 做一个简单的基本变形：

$$f(x)=f(c)+f(x)-f(c)=f(c)+\frac{f(x)-f(c)}{x-c}\cdot (x-c)，此时 x \neq c$$

此时，$x\neq c$，对于上面的变形当然是成立的。那么，当 $x\rightarrow c$ 时，即 x 不断逼近于 c 的时候，等式的左右两侧也是相等的，对应的就是两侧同时取极限：

$$lim{x\rightarrow c}f(x)=lim{x\rightarrow c}[f(c)+\frac{f(x)-f(c)}{x-c}\cdot (x-c)] =lim{x\rightarrow c}f(c)+lim{x\rightarrow c}\frac{f(x)-f(c)}{x-c}\cdot lim_{x\rightarrow c}(x-c)$$

仔细观察一下这个等式中的三部分，其中：

• f(c) 是一个与变量 x 取值无关的常数，因此 $lim_{x\rightarrow c}f(c)=f(c)$。
• 而 $lim{x\rightarrow c}\frac{f(x)-f(c)}{x-c}$ 就是导数 f'(c) 的定义式，而我们前面说了，前提条件是导数 f'(c) 存在，因此 $lim{x\rightarrow c}\frac{f(x)-f(c)}{x-c} = f'(c)$。
• 而最后一个很明显，$lim_{x\rightarrow c}(x-c)=0$。

因此，最终就有：

$$lim{x\rightarrow c}f(x)=lim{x\rightarrow c}f(c)+lim{x\rightarrow c}\frac{f(x)-f(c)}{x-c}\cdot lim{x\rightarrow c}(x-c) =f(c)+f'(c)\cdot 0=f(c)$$

我们只看一头一尾，即：$lim_{x\rightarrow c}f(x)=f(c)$，函数在 c 点处这不就连续了吗。

连续不一定可微

那反过来呢？很多地方最爱区分的概念就是连续一定可微吗？也就是说函数 f(x) 在 c 点处连续，那么导数 f'(c) 一定存在吗？答案是不一定，我们看几个简单的例子。

首先，我们用这个函数来证明：y=|x|。

在 x=0 点处函数显然是连续的，那么函数在这个点的导数存在吗？我们直接扣定义，写出导数的定义式：

$$f'(0)=lim{h\rightarrow 0}\frac{|0+h|-|0|}{h}=lim{h\rightarrow 0} \frac{|h|}{h}$$

这里，当 h 从右侧逼近 0 的时候：即

$$lim_{h\rightarrow 0^{+} } \frac{|h|}{h} = \frac{h}{h}=1$$

而当 h 从左侧逼近 0 的时候，即

$$lim_{h\rightarrow 0^{-} } \frac{|h|}{h} = \frac{-h}{h} = -1$$

此时我们发现左极限和右极限不相等，因此极限 $lim_{h\rightarrow 0} \frac{f(0+h)-f(0)}{h}$ 不存在，换句话说，函数在 0 处的导数 f'(0) 不存在。

从中我们受到启发并进行拓展，一个连续函数在它的图形中有任何尖锐拐角的地方都是不可导的。

如果函数不是这种尖峰形状的，而是光滑的，那又是什么情形呢？

我们再看另一个例子：$y=x^{\frac{1}{3}}$，显然它在点 x=0 的地方是光滑且连续的，但是它的导数为

$$f'(x)=\frac{1}{3}x^{-\frac{2}{3}}=\frac{1}{3x^{\frac{2}{3}}}$$

此时我们发现：

$$lim_{x\rightarrow 0}=\frac{1}{3x^{\frac{2}{3}}}=\infty$$

因此，函数在点 0 处不可导。

连续与可微的概念希望大家能够通过上面的几个小例子加深概念。

一些导数的基本记号

最后，我们来看看导数的一些记号，方便我们在后续的讨论中使用。

首先如果自变量 x 的值从 $x1$ 改变到 $x2$，那么 $x2-x1$ 就叫作 x 的增量，我们把它记作是 $\Delta x$。

相应的，函数的取值 y 也从 $f(x1)$ 变到了 $f(x2)$，那么相应 y 的增量为：$\Delta y=y2-y1=f(x2)-f(x1)$。

因此，假设自变量从 x 变化到 $x+\Delta x$，相应的增量比为：

$$\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}$$

当 $\Delta x\rightarrow 0$ 时，我们也可以用下面的符号来记作其导数：

$$\frac{dy}{dx}=lim{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=lim{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=f'(x)$$

而像一些函数的基本求导法则，高阶导数的求导法则等基础知识，我们就不在课程中过多赘述了，大家可以参照手头的微积分教材进行复习巩固。

基于 Python 的数值微分法

那么在实际的程序中，我们如何来求取函数的导数值呢？很显然，紧扣定义就好了。

接下来我们参照定义式 $\frac{dy}{dx} =lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}$，让 h 取一个非常小的值，利用 Python 来实现函数导数的求取。

但是实际上，在用数值法求近似的导数值的时候，还可以使用中心差分法，这样求得的导数会更接近于真实值，中心差分法求导的定义式为：

$$\frac{dy}{dx}=lim_{h\rightarrow 0}\frac{f(x+\frac{h}{2})-f(x-\frac{h}{2})}{h}$$

中心差分法本质上还是建立在割线的极限是切线的思想，为什么说实际操作时，中心差分法更接近于真实的导数值呢？我们看一个示意图：

从图中可以看出，用中心差分法所做割线的斜率要比普通定义法更接近于真实切线的斜率。

最后，我们用代码来实际进行导数的数值法求解，我们举一个简单的函数 $f(x)=x^2$，它的导数很简单 $f'(x)=2x$，我们比较在 x=4 时，两种方法求出的导数数值近似解，以及和真实值 8 之间的差距。

代码片段：

def function(x):    return x*xdef numerical_diff(f, x):    h = 1e-4    return (f(x+h) - f(x))/hdef numerical_diff_1(f, x):    h = 1e-4    return (f(x+h/2) - f(x-h/2))/hprint('theoretical value={}'.format(2*4))print('value={},error={}'.format(numerical_diff(function, 4),abs(numerical_diff(function, 4)-8)))print('value={},error={}'.format(numerical_diff_1(function, 4),abs(numerical_diff_1(function, 4)-8)))

运行结果：

theoretical value=8value=8.00009999998963,error=9.999998962939571e-05value=7.999999999963592,error=3.6408209780347534e-11

从运行结果中我们可以看出，函数 $f(x)=x^2$ 在 x=4 处的导数理论值为 8，数值求导过程中，定义法求出的导数近似值为 8.00009999998963 ，中心差分法求得的导数近似值为 7.999999999963592，很明显，中心差分法求得的导数近似值更接近于真实的理论值。

[help me with MathJax]

函数近似与泰勒级数

多元函数及其偏导数

多元函数的微分及泰勒近似

多元函数的梯度及其应用

导引：最优化的基本问题和存在条件

一元函数的极值：运用迭代法

多元函数的极值（上）：梯度法基础

多元函数的极值（中）：最速下降法

多元函数的极值（下）：牛顿法与向量微分

阅读全文: http://gitbook.cn/gitchat/column/5ddcf0b079b8c11c31370e76