牛客寒假算法基础训练营4 非官方题解
附官方题解链接
CSDN写博客的自动保存功能呢????写到一半误关网页啥都没了。。哭死
emmmm这场讲道理,签到题真的签到,简单题真的简单,难题真的难得自闭
还好抽中了件T恤压压惊哈哈哈哈
A Applese 的取石子游戏
链接:https://ac.nowcoder.com/acm/contest/330/A
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
Applese 和 Bpplese 在玩取石子游戏,规则如下:
一共有偶数堆石子排成一排,每堆石子的个数为 a i a_i ai。两个人轮流取石子,Applese先手。每次取石子只能取最左一堆或最右一堆,且必须取完。最后取得的石子多者获胜。假设双方都足够聪明,最后谁能够获胜呢?
输入描述:
第一行是一个正偶数 n,表示石子的堆数。
第二行是 n 个正整数 a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an,表示每堆石子的个数。
输出描述:
输出一个字符串“Applese”或“Bpplese”,表示胜者的名字。
示例1
输入
4
2 3 3 3
输出
Applese
备注:
2 ≤ n ≤ 105 2≤n≤105 2≤n≤105
1 ≤ a i ≤ 105 1≤ai≤105 1≤ai≤105
∑ a i ∑ai ∑ai为奇数
博弈题无非是几种情况
- 先手胜(特定问题下)
- 后手胜(特定问题下)
- 除少数情况先手胜
- 除少数情况后手胜
稍难的博弈,如威佐夫博弈123,主要难在确定先手胜的情况和后手胜的情况
但这里显然没有那么多变化,所以只要猜一个先手胜或者先手败就完事了。既然样例是先手胜,那就交一发先手胜AC
那么为什么呢?
首先题目说了有偶数堆石子,且石子总数为奇数。这两个条件就排除了平局的可能性,所以必然是一胜一负
先手要怎么胜呢?
先手必然可以从偶数堆石子中,拿出所有下标为偶数的石子或者所有下标为奇数的石子
比如说总共有10堆石子,那么先手可以选择拿1,3,5,7,9堆或者拿2,4,6,8,10堆,他只要选择更大的那个就行了。(这个不用讲的更详细了吧,不懂自己模拟拿一下也该懂了,他一定能保证拿到所有奇数堆或所有偶数堆)
#includeB Applese 走方格
链接:https://ac.nowcoder.com/acm/contest/330/B
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
Special Judge, 64bit IO Format: %lld
题目描述
精通程序设计的 Applese 又写了一个游戏。
在这个游戏中,它位于一个 n n n 行 m m m 列的方阵中的左上角(坐标为 ( 0 , 0 ) (0, 0) (0,0),行的序号为 0 ∼ n − 1 0∼n−1 0∼n−1,列的序号为 0 ∼ m − 1 0∼m−1 0∼m−1)。
现在它想不重复地走过所有格子(除了起点),最后回到左上角的一个方案。
每次只能往上下左右其中一个方向走一格。
输入描述:
仅一行两个整数 n 和 m,表示方阵的大小。保证大于1×1。
输出描述:
如果存在方案,则输出一行操作,包含"L"、“R”、“U”、“D”,分别表示左、右、上、下。如果有多种方案,输出任意一种即可。
如果没有方案,则在一行中输出"-1"。
示例1
输入
2 2
输出
RDLU
示例2
输入
2 3
输出
RRDLLU
备注:
1 ≤ n , m ≤ 10 1≤n,m≤10 1≤n,m≤10
这个问题还是比较容易想的,如果是奇数行奇数列那么无解,如果是偶数行或者偶数列,那么走蛇形就行
在这里借用一下官方题解的图:
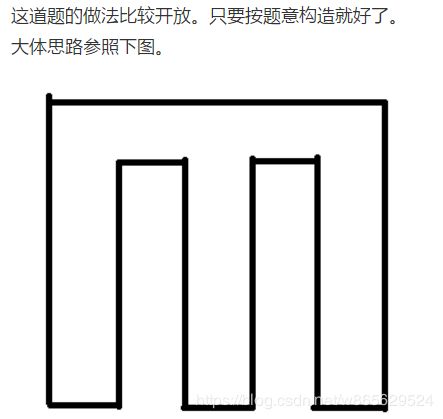
特殊情况是:只有一行或一列时无解
特殊情况中的特殊情况是:1行2列和1列2行这两种情况有解
想到这些这题就容易写了
在这里谈谈证明:有解的情况下,解都能给出来了,那就没啥好证明的了。无解时,只有1行或只有1列也容易理解。所以这里直接讨论奇数行奇数列的普适情况
记奇数行奇数列的点为类型1,其余的点为类型2
那么原来的矩阵按类型标记,就变成了:
1 2 1 . . . 1 2 1 2 . . . 2 1 2 1 . . . 1 . . . . . . . . . . . . . . . 1 2 1 . . . 1 \begin{matrix} 1 & 2 & 1 & ... & 1\\ 2 & 1 & 2 & ... & 2\\ 1 & 2 & 1 & ... & 1\\ ... & ... & ... & ... & ...\\ 1 & 2 & 1 & ... & 1\\ \end{matrix} 121...1212...2121...1...............121...1
显然可以发现,1的个数比2的个数要多1,而且1的四周必定为2,2的四周必定为1
按照题目要求的方式行进,路径必然可以标记为212121…21(不算起始点(0,0))。而我们说1的个数比2要多,所以不可能存在那么一条路径,以2开始,以1结束,且遍历所有的点
emmmmm讲道理比赛的时候哪来那么多时间想这些证明,特判两个样例就当成已知了。。我知道是因为初中的时候网上流行那种一笔画的图,无聊的时候去证明过那个一笔画是不可能的,证明就类似这样。所以才知道
不必太纠结这份代码,反正这种代码一人一个样
#includeC Applese 走迷宫
链接:https://ac.nowcoder.com/acm/contest/330/C
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
精通程序设计的 Applese 双写了一个游戏。
在这个游戏中,它被困在了一个n×m 的迷宫中,它想要逃出这个迷宫。
在迷宫中,有一些方格是水池,只有当 Applese 处于水属性的时候才可以通过;有一些方格是岩浆,只有当 Applese 是火属性的时候可以通过;有一些方格是墙壁,无论如何都无法通过;另一些格子是空地(包括起点和终点),可以自由通过。
在一些空地上有神秘道具可以让 Applese 转换自己的属性(从水属性变为火属性或从火属性变为水属性,需要一个单位的时间)。
已知 Applese 在一个单位的时间内可以朝四个方向行走一格,且开始处于水属性,位于空地的道具拾取后只能在该处立即使用(或者不使用),且可以多次使用。求它走出迷宫需要的最少时间。
输入描述:
第一行两个正整数 n, m 表示迷宫的大小。
接下来 n 行,每行长度为 m 的字符串。描述地图。
其中 ‘S’ 表示起点,‘T’ 表示终点,’.’ 表示空地,‘w’表示岩浆,’~‘表示水池,’@’ 表示道具,’#'表示障碍。
保证地图中的起点和终点只有一个,道具都位于空地。
输出描述:
输出一个整数,表示 Applese 走出迷宫的最短时间。特别地,如果 Applese 走不出迷宫,输出 “-1”。
示例1
输入
5 5
.w@…
.S#…
~w#…
.w…~
@w.~T
输出
18
备注:
1 ≤ n , m ≤ 100 1≤n,m≤100 1≤n,m≤100
走迷宫????最短路????除了BFS还能有什么吗???
本来看题目还有属性啥的那么复杂,还怕搜索搞不过去。后来看一下数据范围。。。100*100,随便怎么搞都过了啊
emmmm那这题要写些什么。。。没啥好写的啊
emmmm写点基础的。。。BFS是广度优先搜索,采用的数据结构是满足先进先出特性的队列。一般的BFS的基本思路是先把距离为0的状态入队,然后把所有距离为i的状态出队,并将这些状态能达到的距离为i+1的状态入队。如果在入队(或出队)过程中发现终点,因为我们是按距离逐渐递增来搜索的,所以第一次出现就必然是最近距离,就可以直接输出结果。如果同一个状态在次入队,为了防止死循环,我们可以采用标记法拒绝其入队,或是在拓展时拒绝将已标记的状态的相邻状态入队。如果队列中的点为空,就代表所有能访问到的点都已经访问过一次了,如果还没到达终点,那就说明终点不可达。
在这题中,Node存储点的坐标和在这点的状态(水或火), v i s [ x ] [ y ] [ s t a ] vis[x][y][sta] vis[x][y][sta]标记以sta的状态访问点(x,y)的情况,q代表储存结点用的队列, p a i r < n o d e , c n t > pair<node, cnt> pair<node,cnt>表示node状态对应的移动步数为cnt
(感觉是废话,已经学过的人不用看,没学过的人看不懂emmmm不过对读代码多多少少有些帮助???)
不过这种类型的搜索对于一个学习算法的人来说还是算非常基础的了
#includeD Applese 填数字
暴力没写过,DP想不到怎么搞。。。完全不会。。。
链接:https://ac.nowcoder.com/acm/contest/330/D
来源:牛客网
时间限制:C/C++ 2秒,其他语言4秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
精通程序设计的 Applese 叒写了一个游戏。
在这个游戏中,有一个n×m 的方格,每个格子只能填入0∼9 这 10 个数字中的一个。要求每两个相邻的格子的数字的和是个素数。
现在已经往格子里面填入了一些数字,没有填入数字的格子显示成 ?,它想知道有多少方案把这些格子填满。
输入描述:
第一行两个整数 n, m。表示 n 行 m 列的格子。
接下来 n 行,每行 m 个字符表示这个方格。
数据保证已经填写数字的格子满足要求。
输出描述:
输出一个整数表示方案数。
示例1
输入
2 2
1?
23
输出
2
备注:
1 ≤ n , m ≤ 6 1≤n,m≤6 1≤n,m≤6
E Applese 涂颜色
链接:https://ac.nowcoder.com/acm/contest/330/E
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
精通程序设计的 Applese 叕写了一个游戏。
在这个游戏中,有一个 n 行 m 列的方阵。现在它要为这个方阵涂上黑白两种颜色。规定左右相邻两格的颜色不能相同。请你帮它统计一下有多少种涂色的方法。由于答案很大,你需要将答案对 1 0 9 + 7 10^9+7 109+7取模。
输入描述:
仅一行两个正整数 n, m,表示方阵的大小。
输出描述:
输出一个正整数,表示方案数对 1 0 9 + 7 10^9+7 109+7取模。
示例1
输入
1 1
输出
2
示例2
输入
2 2
输出
4
备注:
1 ≤ n , m ≤ 1 0 100000 1≤n,m≤10^{100000} 1≤n,m≤10100000
因为只有两种颜色,且左右相邻的两块颜色不能相同。等于说是确定了一行中第一块的颜色,就能确定一整行的颜色。
由于上下相邻的两块没有限制,所以每一块都是独立的两种
那么n行总共就有 2 n 2^n 2n种
推出这个结论并不难,难的是在 n ≤ 1 0 100000 n≤10^{100000} n≤10100000的范围内求
求次幂肯定是用快速幂没的说,但是快速幂第一发容易T,看官方题解是这么说:

指数循环节降幂我猜应该是费马小定理(或者说欧拉定理,费马小是欧拉的特殊情况)的意思,因为1e9+7是质数,那么我们有 a b = a b m o d f a i ( p ) ( m o d p ) a^b=a^{b \ mod \ fai(p)} (mod \ p) ab=ab mod fai(p)(mod p),这里 p = 1 0 9 + 7 p=10^9+7 p=109+7,因为是质数,所以 f a i ( p ) = 1 0 9 + 6 fai(p)=10^9+6 fai(p)=109+6
用费马小定理再用快速幂,和直接用快速幂,将复杂度从O(logn)优化到了O(log(n%mod)),看起来好像是同一个量级的,只是这里的n有100000位,mod只有9位,相差已经足以将量变转换为质变了。如果不带这个优化的话,用2的幂来算,乘10个2相当于乘1024,相当于位数+3,所以中间差的运算次数大约在(100000-9)/3*10这么多次,而且每次运算都是大数运算,大数运算里面还有一个复杂度。所以总的来说优化幅度还是挺大的
嗯大数用python或java
import math
n, m = input().split(" ")
n = int(n) % 1000000006
ans = 1
t = 2
while(n >= 1):
if(n&1 == 1):
ans = ans*t%1000000007
t = t*t%1000000007
n = n >> 1
print(ans)
F Applese 的QQ群
链接:https://ac.nowcoder.com/acm/contest/330/F
来源:牛客网
时间限制:C/C++ 2秒,其他语言4秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
Applese 有一个QQ群。在这个群中,大家互相请教问题。如 b 向 a 请教过问题,就把 a 叫做是 b 的"老板"。这样一个群中就会有很多老板。
同时规定:如果 a 是 b 的老板,b 是 c 的老板,那么 a 也是 c 的老板。
为了不破坏群里面和谐交流的氛围,Applese 定了一个群规:不允许出现 a 既是 b 的老板, b 又是 a 的老板。
你需要帮助 Applese 判断大家是否遵守了群规。
输入描述:
第一行两个整数 n, m,表示群里的人数以及请教问题的数量。
接下来 m 行,每行两个整数 a, b,表示 a 是 b 的"老板",即 b 向 a 请教了一个问题。
注:无论是否违反了群规,a 都会成为 b 的老板。
输出描述:
对于每次提问,输出一行"Yes"表示大家都遵守了群规,反之输出"No"。
示例1
输入
4 4
1 2
2 3
3 1
1 4
输出
Yes
Yes
No
No
备注:
1 ≤ n ≤ 105 1≤n≤105 1≤n≤105
1 ≤ m ≤ 2 ⋅ 105 1≤m≤2⋅105 1≤m≤2⋅105
1 ≤ a , b ≤ n 1≤a,b≤n 1≤a,b≤n
这题搞了好久,第一眼以为是傻逼并查集,后来发现我自己是个傻逼。
不能用并查集的理由是:并查集只有若干条链式关系,但是这个问题背景下,一个人可以有多个老板,多个人也可以共享一个老板,所以只能当做图论来处理
显然这是个判环的问题。乍一眼还以为是在线判环,后来问了下,回答说输出第一个No之后,所有的询问均输出No。那么这就是一个离线问题了。先把图离线下来,再找环,再找出现最早的环中,出现最晚的边。然后在这条边出现之前输出Yes,在这条边出现之后输出No
写了个tarjan,但是告诉我MLE,有点崩溃。。。并不明白这份代码为什么会MLE。。。
答案说是二分+拓扑,那我也能理解吧。只是不知道我这份代码何德何能领一份MLE
dalao帮忙看看????
嗯这份代码没AC
#includeG Applese 的毒气炸弹
链接:https://ac.nowcoder.com/acm/contest/330/G
来源:牛客网
时间限制:C/C++ 2秒,其他语言4秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
众所周知,Applese 是个很强的选手,它的化学一定很好。
今天他又AK了一套题觉得很无聊,于是想做个毒气炸弹玩。
毒气炸弹需要 k 种不同类型元素构成,Applese一共有 n 瓶含有这些元素的试剂。
已知元素混合遵循 m 条规律,每一条规律都可以用 “x y c” 描述。
表示将第 x 瓶试剂混入第 y 瓶试剂或者把第 y 瓶试剂混入第 x 瓶试剂,需要消耗 c 的脑力。
特别地,除了这 m 条规律外,Applese 可以将任意两瓶相同元素的试剂混合,且不需要消耗脑力。
Applese 想要配出毒气炸弹,就需要使 S 中含有1∼k 这 k 种元素。它想知道自己最少花费多少脑力可以把毒气炸弹做出来。
输入描述:
第一行为三个整数 n, m, k 表示 Applese 拥有的试剂的数量,混合规律的数量和所需的元素种类数。
第二行为 n 个整数 a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an,分别表示每一瓶试剂的元素类型。
接下来m行,每行三个整数 x, y, c,含义如题目描述中所述。不保证 x, y的试剂种类不同。
输出描述:
输出一个正整数表示最小的耗费脑力。特别地,如果无法合成出毒气炸弹,输出 “-1”。
示例1
输入
6 8 2
1 1 1 2 2 2
1 2 1
2 3 2
1 3 3
3 4 6
4 5 1
4 6 3
5 6 2
1 6 2
输出
2
备注:
1 ≤ n , k , m ≤ 105 1≤n,k,m≤105 1≤n,k,m≤105
1 ≤ x , y ≤ n , x ≠ y 1≤x,y≤n,x≠y 1≤x,y≤n,x̸=y
1 ≤ c ≤ 1 0 9 1≤c≤10^9 1≤c≤109
emmmm这题看了题但是没做,答案说是直接求MST,emmmm后悔没仔细想
H Applese 的大奖
链接:https://ac.nowcoder.com/acm/contest/330/H
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
Applese 和它的小伙伴参加了一个促销的抽奖活动,活动的规则如下:有一个随机数生成器,能等概率生成0∼99 之间的整数,每个参与活动的人都要通过它获取一个随机数。最后得到数字最小的 k 个人可以获得大奖。如果有相同的数,那么后选随机数的人中奖。
Applese 自然是最心急的一个,它会抢在第一个去按随机数。请你帮忙计算一下它能够中奖的概率。
输入描述:
仅一行三个正整数 n, k, x,分别表示参与抽奖的总人数(包括Applese),中奖的人数和 Applese 获得的随机数。
输出描述:
输出一个正整数表示 Applese 中奖的概率 m o d 1 0 9 + 7 mod \ 10^9+7 mod 109+7。
即如果概率等于 a b ab ab, a , b ∈ N a,b∈N a,b∈N 且 g c d ( a , b ) = 1 gcd(a,b)=1 gcd(a,b)=1,你需要输出一个自然数 c < 109 + 7 c<109+7 c<109+7 满足 b c ≡ a ( m o d 1 0 9 + 7 ) bc≡a \ (mod \ 10^9+7) bc≡a (mod 109+7)
示例1
输入
1 1 99
输出
1
示例2
输入
2 1 38
输出
770000006
示例3
输入
6 2 49
输出
687500005
备注:
1 ≤ n ≤ 109 1≤n≤109 1≤n≤109
1 ≤ k ≤ m i n n , 105 1≤k≤min{n,105} 1≤k≤minn,105
0 ≤ x ≤ 99 0≤x≤99 0≤x≤99
这题的公式好推,应该有点数学功底的人都推出来了。但是要求逆元,有求逆元的要求还要求组合数,这就有点小细节了。所以一直在纠结别的题,没看这个。。。嗯应该知道公式就能写吧,像我这样基础不扎实的话还是老老实实看std吧
把公式放这:
a n s = Σ i = 0 k − 1 C n − 1 i ( x + 1 100 ) i ( 100 − ( x + 1 ) 100 ) n − i − 1 ans = \Sigma_{i=0}^{k-1}C_{n-1}^{i}(\frac{x+1}{100})^i(\frac{100-(x+1)}{100})^{n-i-1} ans=Σi=0k−1Cn−1i(100x+1)i(100100−(x+1))n−i−1
I Applese 的回文串
链接:https://ac.nowcoder.com/acm/contest/330/I
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
自从 Applese 学会了字符串之后,精通各种字符串算法,比如……判断一个字符串是不是回文串。
这样的题目未免让它觉得太无聊,于是它想到了一个新的问题。
如何判断一个字符串在任意位置(包括最前面和最后面)插入一个字符后能不能构成一个回文串?
输入描述:
仅一行,为一个由字母和数字组成的字符串 s。
输出描述:
如果在插入一个字符之后可以构成回文串,则输出"Yes", 否则输出"No"。
示例1
输入
applese
输出
No
示例2
输入
java
输出
Yes
备注:
∣ s ∣ ≤ 1 0 5 |s|≤10^5 ∣s∣≤105
求回文串直接求的话一般就是manacher吧,但是马拉车不支持带修改啊,想都不会往那边想。。。
所以肯定是用双指针从左右两个开始判断,判断到不相等就一定要使用一次操作。
因为只有一次操作机会,所以递归深度不会太深。粗略估计直接写递归理论复杂度不会超过O(3n),如果把递归的树画出来,会发现所有的叶结点离主干(嗯没有这个名词我只是不知道用哪个词来形容,懂就好了)的距离不会超过2,所以总的结点个数应该不会超过3n。所以我就直接递归了。
可以写递归过的话那就很好写了啊
#includeJ Applese 的减肥计划
链接:https://ac.nowcoder.com/acm/contest/330/J
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
Special Judge, 64bit IO Format: %lld
题目描述
Applese 最近又长胖了,于是它打算减肥——练习举重。
他在举重的时候用两只手往不同方向用力,从而把杠铃举起来。
已知 Applese 两只手分别产生的力的大小,以及它们之间的夹角,试求两力合力的大小。
输入描述:
仅一行三个整数 f 1 , f 2 , a f1,f2,a f1,f2,a,分别表示两只手产生的力的大小以及它们之间的夹角。
输出描述:
输出一个实数表示两力合力的大小,要求相对误差或绝对误差不超过 1 0 − 6 10^{−6} 10−6。
严格来讲,如果你的答案是 a,而标准答案是 b,那么当 ∣ a − b ∣ m a x { 1 , ∣ b ∣ } ≤ 1 0 − 6 |a−b|max\{1,|b|\}≤10^{−6} ∣a−b∣max{1,∣b∣}≤10−6 时,你的答案会被认为是正确的。
示例1
输入
6 8 90
输出
10.0000000000
示例2
输入
10 10 60
输出
17.3205080757
备注:
1 ≤ f 1 , f 2 ≤ 100 1≤f1,f2≤100 1≤f1,f2≤100
0 ≤ a ≤ 180 0≤a≤180 0≤a≤180
这。。。不是个纯几何题嘛。。。
学过物理的都知道,力的合成遵循平行四边形定则。emmmm不过这题用三角形定则比较好解释吧,将F1和F2首尾相连,从F1的起点到F2的终点的长度就是合力的大小,给出的角度 a a a是F1和F2的夹角,在几何上表现为三角形的外角,其对应的内角为 180 − a 180-a 180−a,其所对的边恰好为合力
已知两角一边求第三边长,余弦定理啊。。。。
a n s = f 1 2 + f 2 2 − 2 f 1 f 2 c o s ( 180 − a 180 P I ) ans = \sqrt{f_1^2+f_2^2 - 2f_1f_2cos(\frac{180-a}{180}PI)} ans=f12+f22−2f1f2cos(180180−aPI)
注意cos默认是弧度制,而给出的数据是角度制,要转换一下
#include