二维线段树专题
二维线段树
二维线段树最主要用于平面统计问题。类似一维线段树,最经典的就是求区间最值(或区间和),推广到二维,求得就是矩形区域最值(或矩形区域和),对于矩形区域和,二维树状数组更加高效,而矩形区域最值,更加高效的方法是二维RMQ,但是二维RMQ不支持动态更新,所以二维线段树还是有用武之地的。
如果对一维线段树已经驾轻就熟,那么直接来看下面两段对比,就可以轻松理解二维线段树了。
一维线段树是一棵
二叉树,树上每个结点保存
一个区间和一个域,非叶子结点一定有
两个儿子结点,儿子结点表示的
两个区间交集为空,并集为父结点表示的
区间;叶子结点的表示区间长度为1,即单位长度;域则表示了需要求的数据,每个父结点的域可以通过
两个儿子结点得出。
二维线段树是一棵
四叉树,树上每个结点保存
一个矩形和一个域,非叶子结点一定有
二或四 个儿子结点,儿子结点表示的
四个矩形交集为空,并集为父结点表示的
矩形;叶子结点表示的矩形长宽均为1,域则表示了需要求的数据,每个父结点的域可以通过
四个儿子结点得出。
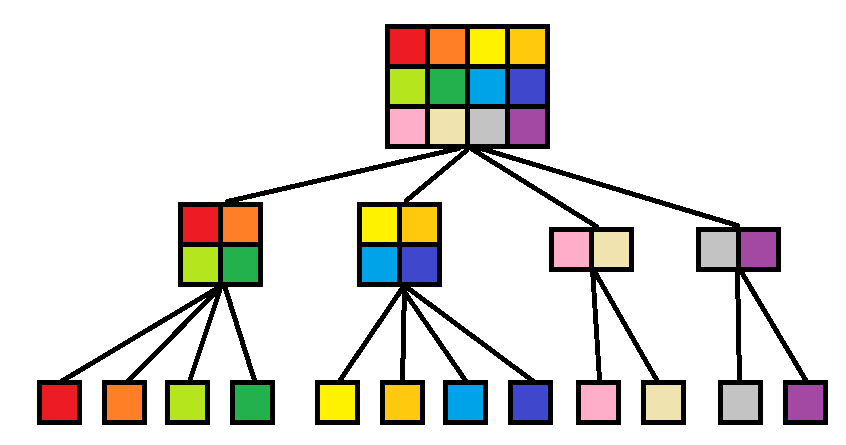
图1
图1中,每个叶子结点的单位面积为1,非叶子结点表示的矩形进行四分后,如图2所示,四个子矩形分别表示的是儿子结点表示的矩形区域。特殊的,当矩形面积为1 X H或者W X 1的时候,变成了一维的情况,这就是为什么有些结点有四个子结点,而有些结点只有两个子结点的原因了。
图2
基本结构已经清楚了,按照惯例,要介绍一下时空复杂度。
首先来看空间复杂度,一个 W x H 的矩形,根结点表示的矩形是W x H,令N = max{W, H},那么这棵二维线段树的深度D = log2(N)+1,当这棵树是一棵满四叉树的时候,结点数达到最大值,根据等比数列求和公式,最大情况的结点数为 (4^D - 1) / 3。更加直观的,当N = W = H = 2^k, 必定是一棵满四叉树,结点数为(4^D-1) / 3 = ( 4^(k+1) - 1 ) / 3 = (2^(2k+2)-1) / 3,去掉分子上的零头1,约等于(4/3)*N^2, 所以空间复杂度为O(N^2)。
再来看时间复杂度,需要分情况:
建树:建树时必定访问到每个结点,而且都是访问一次,所以建树的复杂度为O(N^2);
单点更新:每次更新一个单位矩形的值,访问时只会访问从树的根结点到叶子结点的一条路径,所以单点更新的复杂度为O( log2(N) )。
区域询问:情况类似一维的区间询问。从根结点开始拆分区域,当询问区域完全覆盖结点区域时,不需要递归往下走,总体复杂度是
O( log2(N) * log2(N) ) ? 这里还是打个问号先,具体是一个log还是两个log记不清了,找个时间证明一下,可以肯定的是,不会退化成O(N)。
接下来看看每个树结点需要保存一些什么信息, 以最值为例,除了保存最值以外,有可能需要知道这个最值在整个矩形的具体坐标,所以我们的最值信息dataInfo需要保存三个信息,posx和posy表示最值的具体位置,val保存最值,由于二维线段树的空间复杂度为O(N^2),所以坐标信息不会很大,为了尽力节省内存,坐标值用short来存即可。最值val的话看实际情况而定,一般用int就够了。
treeNode则是线段树结点的结构体,其中成员由dataInfo对应的最值和son[4]表示的子结点编号组成,我们的线段树结点采用静态结点,即每个线段树结点都对应静态数组
nodes中的某个元素,便于通过编号在O(1)的时间内获取到对应树结点的指针,son[4]记录了四个子结点在nodes中的下标。仔细观察可以发现,如果对于一棵线段树,保证所有结点编号都连续的情况下,如果父结点的编号确定,那么子结点的编号也就确定了。例如,根结点编号为1,那么四个子结点编号为2、3、4、5,父结点编号为2,四个子结点的编号为6、7、8、9,根据数学归纳法,当结点编号为p,那么它的四个子结点编号为(4*p-2+x),其中x取值为[0, 3],所以四个子结点的编号信息可以通过O(1)的时间计算出来,就不用存储在线段树结点上了,大大节省了内存开销。
结构定义代码如下:
#define LOGN 10
#define MAXN (1<<LOGN)
#define MAXNODES 3*(1<<(2*LOGN)/4 + 100)
#define son(x) (p*4-2+x)
// 最值信息
struct dataInfo {
short posx, posy;
int val;
dataInfo() {
posx = posy =
val = -1;
}dataInfo(short _posx, short _posy, int _val) {
posx = _posx;
posy = _posy;
val = _val;
}
};
// 线段树结点信息
struct treeNode {
// int son[4]
dataInfo maxv, minv;
void reset() {
maxv = dataInfo(0, 0, INT_MIN);
minv = dataInfo(0, 0, INT_MAX);
}
}nodes[ MAXNODES ];
// 注意,这里需要返回指针,因为在后续使用中需要对这个结点的信息进行改变,如果返回对象的话只是一个copy,不会改变原结点的内容
treeNode* getNode(int id) {
return &nodes[id];
}
这时候,我们发现线段树的结点上还缺少一个很重要的信息,因为每个结点表示了一个矩形区域,那为什么没有存下这个矩形区域呢?毋庸置疑,也是为了节省内存,在接下来的区域查询、单点更新的介绍中会讲到,这个区域其实在每次递归的时候是作为传参进入函数内部的,结点编号确定,矩形区域就确定了,所以没必要存储在结点中。
为了处理方便,我们还需要封装一个区间类(由于矩形可以表示成两个不同维度的区间,所以这里只需要封装一个区间类即可,矩形类的操作没有区间内那么简单,一目了然),它支持一些基本操作,如判交、判包含、取左右半区间等等、,具体代码如下:
struct Interval {
int l, r;Interval() {}
Interval(int _l, int _r) {
l = _l;
r = _r;
}
// 区间中点 int mid() {
return (l + r) >> 1;
}
// 区间长度
int len() {
return r - l + 1;
}
// 左半区间
Interval left() {
return Interval(l, mid());
}
// 右半区间
Interval right() {
return Interval(mid()+1, r);
}
// 区间判交
bool isIntersectWith( Interval& tarI ) {return !( l > tarI.r || r < tarI.l );
}
// 区间判包含
bool isInclude( Interval& tarI ) {return l <= tarI.l && tarI.r <= r;
}
bool in (int v) {return l <= v && v <= r;
}
};
那么接下来就是建树了,建树就是递归生成结点的过程,这里的生成并非创建,原因是因为我们的结点是静态的。每建一次树,只是把所有线段树结点的信息进行一次重置,对于一个W x H的矩形,假定它的两个对角线坐标为(1, 1) - (W, H),那么我们首先将它切割成四个矩形,令WM = (1+W)/2, HM = (1+H)/2对角线坐标分别为:
(1, 1) - (WM, HM)
(WM+1, 1) - (W, HM)
(1, HM+1) - (WM, H)
(WM+1, HM+1) - (W, H)
图3
这个切割过程是递归进行的,当某次切割的矩形为单位面积的时候,即为递归出口。当然还有一种情况,就是当某次切割后的矩形的某一维为1,而另一维大于1时,这里假设W = 1,H > 1,那么继续切割时会发现WM+1 > W,导致 (WM+1, 1) - (W, HM) 和 (WM+1, HM+1) - (W, H) 这两个矩形面积为负,所以在递归入口处需要判断是否有某一维的右端点小于左端点,如果有,这种矩形是不合法的,不能做为线段树的结点,不需要继续往下递归创建。
建树代码如下:
void build_segtree(int p, Interval xI, Interval yI) {
return ;
}
treeNode* now = getNode(p);
return ;
}
build_segtree( son(0), xI.left(), yI.left() );
build_segtree( son(1), xI.right(), yI.left());
build_segtree( son(2), xI.left(), yI.right() );
build_segtree( son(3), xI.right(), yI.right());
// 空矩形(右端点小于左端点)
if(xI.len() <= 0 || yI.len() <= 0) {return ;
}
treeNode* now = getNode(p);
// 结点初始化
now->reset();
// 单位矩形
if(xI.len() == 1 && yI.len() == 1) {return ;
}
build_segtree( son(0), xI.left(), yI.left() );
build_segtree( son(1), xI.right(), yI.left());
build_segtree( son(2), xI.left(), yI.right() );
build_segtree( son(3), xI.right(), yI.right());
}
其中p为当前线段树结点的编号,son(0) - son(3)则是作为子结点编号穿参进入切割后的矩形
, getNode(p)用于获取编号为p的结点的结构指针,建树的目的就是为每个结点进行初始化,如果求的是最大值,那么将结点上的域都设成 INT_MIN ( 只要比所有接下来要插入的值小即可 ),如果求的是最小值,那么结点上的域都设成 INT_MAX( 只要比所有接下来要插入的值大即可 )。
建树完毕后,这些结点都有了一个初始值,那么接下来就是需要在矩形的每个点插入一个值,然后更新线段树上每个结点的最值信息了。
插入过程和建树过程的思想是一致的,同样是将矩形切割成四份,因为插入的是一个点,所以不可能同时存在于任意两个矩形中(因为是个矩形是互不相交的),所以每次四分只会选择一个矩形进行插入,为了让代码简介,我们还是先将矩形进行切割,然后模拟所有的矩形都能够插入,然后在递归入口处判断该点是否在矩形区域中,如果不在矩形区域直接返回。这样,当递归到单位矩形的时候,这个点的坐标一定是和矩形的坐标重合的,就可以直接更新该矩形所在的线段树结点的域信息了,更新完这个单位矩形还不够,还需要将信息传递给它的父结点,因为每次更新只有一个点,所以改变的结点只有从这个单位矩形所在结点到根结点的一条路径上的结点,所以复杂度是树的深度,即O(log2(N))。
插入结点(单点更新)代码如下:
bool insert_segtree(int p, Interval xI, Interval yI, int x, int y, int val) {
if(xI.len() <= 0 || yI.len() <= 0) {
return false;
}
if( !xI.in(x) || !yI.in(y) ) {
return true;
}
treeNode *now = getNode(p);
if(xI.len() == 1 && yI.len() == 1) {
now->maxv = now->minv = dataInfo(x, y, val);
return true;
}
bool isvalid[4];
isvalid[0] = insert_segtree( son(0), xI.left(), yI.left(), x, y, val );
isvalid[1] = insert_segtree( son(1), xI.right(), yI.left(), x, y, val );
isvalid[2] = insert_segtree( son(2), xI.left(), yI.right(), x, y, val );
isvalid[3] = insert_segtree( son(3), xI.right(), yI.right(), x, y, val );
// 通过四个子结点的信息更新父结点
now->maxv = dataInfo(0, 0, MIN_VAL);
now->minv = dataInfo(0, 0, MAX_VAL);
int i;
for(i = 0;i < 4; i++) {
if( !isvalid[i] ) continue;
treeNode *sonNode = getNode(son(i));
now->maxv = sonNode->maxv.val > now->maxv.val ? sonNode->maxv : now->maxv;
now->minv = sonNode->minv.val < now->minv.val ? sonNode->minv : now->minv;
}
return true;
if(xI.len() <= 0 || yI.len() <= 0) {
return false;
}
if( !xI.in(x) || !yI.in(y) ) {
return true;
}
treeNode *now = getNode(p);
if(xI.len() == 1 && yI.len() == 1) {
now->maxv = now->minv = dataInfo(x, y, val);
return true;
}
bool isvalid[4];
isvalid[0] = insert_segtree( son(0), xI.left(), yI.left(), x, y, val );
isvalid[1] = insert_segtree( son(1), xI.right(), yI.left(), x, y, val );
isvalid[2] = insert_segtree( son(2), xI.left(), yI.right(), x, y, val );
isvalid[3] = insert_segtree( son(3), xI.right(), yI.right(), x, y, val );
// 通过四个子结点的信息更新父结点
now->maxv = dataInfo(0, 0, MIN_VAL);
now->minv = dataInfo(0, 0, MAX_VAL);
int i;
for(i = 0;i < 4; i++) {
if( !isvalid[i] ) continue;
treeNode *sonNode = getNode(son(i));
now->maxv = sonNode->maxv.val > now->maxv.val ? sonNode->maxv : now->maxv;
now->minv = sonNode->minv.val < now->minv.val ? sonNode->minv : now->minv;
}
return true;
}
可以发现,插入的核心代码和建树是一致的,但是这里的插入操作,返回了一个值,表示的是当前插入的线段树结点p是否合法,因为我们在插入的时候无论如何都会将矩形切割成四份,没有去考虑上文中提到的有一维为1的情况,父结点的域值是通过子结点回溯上来进行更新的,如果子结点不合法,不应该作为更新的依据,所以作为父结点,需要知道哪些结点是不合法的。
有了更新,当然需要询问,没有询问,更新也就失去了意义。
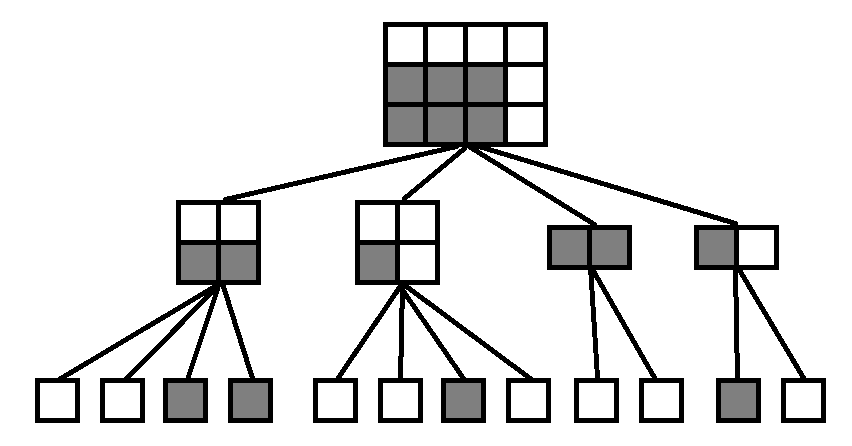
询问一般是区域询问(单点询问就没必要用线段树了),如图4所示,在一个4 x 3的矩形中,需要询问灰色的矩形(3 x 2的矩形,以下统一称为询问矩形)中最大的数是什么。首先来说说原理,同样,和建树以及插入操作一样,我们首先不断将矩形进行切割,每当访问到一个结点的时候将询问矩形和结点矩形进行判交测试,一共有以下几种情况:
1、询问矩形 和 结点矩形 没有交集 (图4中所有白色的叶子结点);
2、询问矩形 完全包含 结点矩形 (图4中根结点的第三个子结点);
3、询问矩形 不完全包含 结点矩形,并且存在交集(图4中根结点的第一、二、四个子结点);
首先我们需要保存一个全局最大值信息,这个信息可以通过引用的方式传递到函数中去,在递归的过程中不断迭代更新;
对于第1、2两种情况都是不需要继续往下递归的,第1种情况不会影响目前的最大值,第2种情况需要将结点上的最大值和全局最大值进行比较,保留大的那个;第三种情况有交集,所以我们需要将矩形继续分割,直到出现第1或者第2种情况为止,而且一定是可以出现的。
图4
区域询问代码如下:
// query_type 0 最大值 1最小值
void query_segtree(int p, Interval xI, Interval yI, Interval tarXI, Interval tarYI, dataInfo& ans, int query_type) {
if(xI.len() <= 0 || yI.len() <= 0) {return ;
}
if( !tarXI.isIntersectWith(xI) || !tarYI.isIntersectWith(yI) ) {
return ;
}
treeNode *now = getNode(p);
// 最大值优化
if(query_type == 0 && ans.val >= now->maxv.val
) {
return ;
}
// 最小值优化
if(query_type == 1 && ans.val <= now->minv.val) {return ;
}
if(tarXI.isInclude(xI) && tarYI.isInclude(yI)) {
if(query_type == 0) {
ans = now->maxv;
}else {
ans = now->minv;
}
return ;
}
query_segtree( son(0), xI.left(), yI.left(), tarXI, tarYI, ans, query_type );
query_segtree( son(1), xI.right(), yI.left(), tarXI, tarYI, ans, query_type );
query_segtree( son(2), xI.left(), yI.right(), tarXI, tarYI, ans, query_type );
query_segtree( son(3), xI.right(), yI.right(), tarXI, tarYI, ans, query_type );
}
这里加入了一个query_type,表示求的是最大值还是最小值,因为有的时候既需要知道最大值,又需要知道最小值,为了简化函数个数引入的一个变量。这里我们发现,当求最大值的时候,如果 询问矩形 和 结点矩形 是有交集并且并非完全包含的情况下,如果结点最大值比全局最大值(以上代码中的ans即全局最大值信息)还小,那么没必要再往下递归了,因为递归下去的最大值不会比当前结点的最大值大,这个优化很重要。
以上就是二维线段树通过三个函数实现求区域最值的全部内容,建树
(build_segtree)、插入
(
insert_segtree
)
、询问
(
query_segtree
),其实当我们将这三个函数中的 yI 这个区间变成[1, 1]的时候,就变成了一维线段树的模板了。