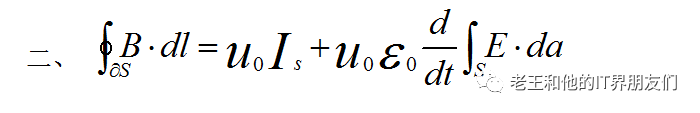机器视觉——麦克斯韦方程组

光，是一种电磁波，这是一件多么奇妙的事情，在我们的周围，我们这个世界，整个宇宙，充斥着这种电磁波。

光的“波粒二相性”决定了它既具有波的特性，又由粒子组成。

组成光的光子，是一种无质量但带有能量的粒子。这种粒子充斥着整个宇宙，被物体吸收或反射，形成万事万物的色彩，进入我们的眼帘，为我们的视觉神经系统所感知，从而在大脑中形成电信号，于是我们又多了一条探索事物的途径。

哲学和数学，从思维和形式上描述了了事物的规律，也是我们探索自然和宇宙的有效工具。

1864年，33岁的麦克斯韦，提出：“光与磁是同一物质的两种属性，而光是按照电磁定律在电磁场中传播的电磁扰动。”

麦克斯韦的物理学思想让宇宙万物展示出它本质的光芒，使得一批又一批的物理学家为之迷思疯狂。

麦克斯韦方程组，总结了前人的科学成果，将电磁现象归纳4个线性偏微分方程式。

   在说明麦克斯韦方程组之前，我们先回顾一下中学知识：单个正/负电荷Q，释放出的电场，我们可以用如下图所示的电力线表示

通过任一封闭曲面的电通量，与该封闭曲面包裹的电荷数成正比

空间中一个电荷，在它周围释放出电场，我们可以通过“电力线”来描述电场。用任意封闭曲面包裹住这个电荷，那么不论这个表面如何膨胀或缩小，通过它表面的电力线是一定的。

同理，假如这个封闭表面内有多个电荷，那么它们释放出的电力线的叠加，就是通过该曲面的所有电力线，我们叫做通过该曲面上的电通量

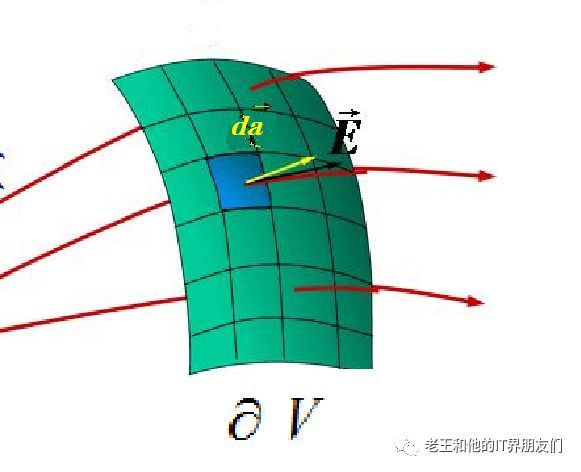
以下图展示封闭包裹空间V的封闭曲面的一部分

磁场在任一表面边缘的环量，和其中穿过的电流强度成正比，同时和该表面电通量的单位时间内的变化成正比。

我们可以理解为：电流产生磁场，同时变化的电场也能产生磁场

中学时我们学到到电流是自由电荷在导体中的定向移动。著名的安培定律是该方程的一部分，我们知道电流可以在它的周围产生环绕的磁场。而麦克斯韦在安培定律的基础上，发现电场的变化也可以产生磁场。于是就总结有以上公式。

以下是某一圆形表面S，其中有在它中间穿越过的电流（我们可以把它想象为导线的横截面）；另外还有穿过该圆形区域的电力线（我们在此以多个点来表示穿越而出的电力线），电力线的总和就是该区域的电通量；电通量单位时间内的变化产生磁场,蓝色部分为磁场在某点处的方向。

通过任一封闭曲面的磁通量，为0。

因为不存在“磁荷”，不能像电荷一样扩散出电场，所以磁力线是封闭的曲线。即：通过任一封闭曲面的磁力线，有“来”必有“去”，正负抵消，整体通过封闭曲面的磁通量为0。

以下是以地球磁场穿越地球表面来说明这一公式的含义。

电场在任一表面边缘的环量，等于单位时间内通过该曲面的磁通量变化。

我们同样可以把它理解为：变化的磁场产生电场。

除去系数，该公式类似于“公式二”中“变化的电场产生磁场”那一部分。

以下是通过某一表面的磁通量和其周围的环形电场之间的关系。

其实中学我们已经学到过，磁通量的变化使环绕它的导线产生电流，我们现在把导线拿掉，于是它就产生了电场。

至此为止，我们简要梳理了麦克斯韦方程组。它们在一定条件下可以解释所有的电磁现象。我们所忽略的几个系数分别什么意义？它们如何影响麦克斯韦方程组发挥其作用？既然光是一种电磁波，那么这些场的变化规律又和具体电磁波有何关系？

我们将在以后的探讨中继续。