leetcode难题之N-Queens

N-Queens问题是回溯法的典型问题，之前的博客有提到，不过觉得有些不完善，刚好这边的leetcode也刷到了就再拿出来总结一遍。

一，题目简述

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

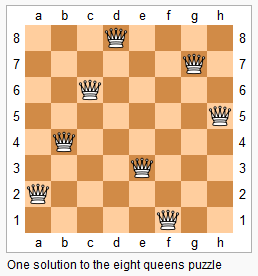
大意就是n皇后游戏，棋盘上每个皇后之间不能在同一行同一列同一对角线，求n皇后游戏可行解的输出。测试样例见leetcode第51题。

二，题目分析

回溯法

n皇后问题的解法有很多，不过面试或笔试题要解的肯定是回溯法。回溯法是一种很简单的算法，大意就是你把求解的过程扔给回溯函数，算法会自动查找可行解并判断是否满足条件，最终给出全部的可行解。就像找丢掉的钥匙一样，我们要从当前的地方开始找然后一点点排查，往回回忆去过的地方，最后找到钥匙。

其实回溯法是有模板的，在方法中首先设定一个目标，判断当前状态是否已经满足了条件，如果没有，进入循环条件先做下一个决定，然后判断它是否有效（有效回溯，没有效跳过），然后撤销做的决定，向下循环。

即{Goal -> {choice -> validate -> undo choice}}

三，题目解答

我的解法：不是时间空间复杂度的最优解，不过尽量贴合模板解法

class Solution {
    public List> solveNQueens(int n) {
        List> res = new ArrayList<>();
        if(n <= 0)
            return res;
        backtrack(n,0,new ArrayList(),res);
        return res;
    }
    
    public void backtrack(int n, int row, List subList, List> res){
        if(row == n){    //Goal
            res.add(new ArrayList<>(subList));
        }else{
            for(int col = 0; col < n; col++){
                subList.add(constructStr(n,col));    //choice
                if(isValid(subList)){    //validate
                    backtrack(n,row+1,subList,res);
                }
                subList.remove(subList.size()-1);    //undo choice
            }
        }
    }
    
    public boolean isValid(List subList){
        int col = subList.size()-1;
        for(int i = 0; i < col; i++){
            int diff = Math.abs(subList.get(i).indexOf('Q') - subList.get(col).indexOf('Q'));
            if(diff == 0 || diff == col - i){
                return false;
            }
        }
        return true;
    }
    
    public String constructStr(int n, int col){
        StringBuilder sb = new StringBuilder();
        for(int i = 0; i < n; i++){
            if(i == col)
                sb.append("Q");
            else
                sb.append(".");
        }
        return sb.toString();
    }
}

在leetcode52 题中，有N-Queen问题的简化版，也是hard难度，问题实质没变，只是输入输出有简化，输入n输出可行解的个数。

不过52题更容易在笔试面试题出现，也启发我们怎么去面对一个稍有变型简化版的回溯法问题

我的解法：

class Solution {
    public int totalNQueens(int n) {
        List> res = new ArrayList<>();
        if(n <= 0)
            return res.size();
        backtrack(n,0,new ArrayList(), res);
        return res.size();
    }
    
    public void backtrack(int n, int row, List tmpList, List> res){
        if(row == n){    //goal
            res.add(new ArrayList<>(tmpList));
        }else{
            for(int col = 0; col < n; col++){
                tmpList.add(col);    //choice
                if(isValid(tmpList)){    //validate
                    backtrack(n,row+1,tmpList,res);
                }
                tmpList.remove(tmpList.size()-1);    //undo choice
            }
        }
    }
    
    public boolean isValid(List tmpList){
        int col = tmpList.size()-1;
        for(int i = 0; i < col; i++){
            int diff = Math.abs(tmpList.get(i) - tmpList.get(col));
            if(diff == 0 || diff == col - i){
                return false;
            }
        }
        return true;
    }
}

四，题目回忆

我们解决了经典回溯法N皇后的两个问题，得出了一个解决回溯法的模板。回溯法是一个很有用的求解全部可行解的方法，如果不要求时间复杂度的话，学会回溯法会成为笔试题的大杀器。还可以求解的问题如求解数组中所有集合个数等，只不过要稍微改变我们的choice和undo的过程增加一些限定条件，然后改良validate函数就可以。

不过我们虽然有了模板，应对一些回溯法的难题还是要多练多想，训练自己解决问题的能力，举一反三。